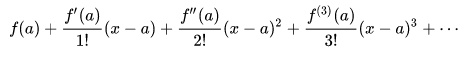Difference between revisions of "Rafi Ahmad Eshandra"
Rafieshandra (talk | contribs) (→KEGIATAN DIKELAS) |
Rafieshandra (talk | contribs) (→KEGIATAN DIKELAS) |
||
| Line 26: | Line 26: | ||
| − | Materi yang diberikan pada pertemuan kali ini adalah '''Metode Taylor''' dimana metode ini berfungsi untuk mengaproksimasikan nilai dari sebuah fungsi. | + | Materi yang diberikan pada pertemuan kali ini adalah '''Metode Taylor''' dimana metode ini berfungsi untuk mengaproksimasikan nilai dari sebuah |
| + | |||
| + | fungsi. | ||
Dalam hal ini deret tersebut merupakan jumlah tak hingga dari suku pada deret. | Dalam hal ini deret tersebut merupakan jumlah tak hingga dari suku pada deret. | ||
Untuk menghitungnya digunakan dengan prinsip turunan pada sebuah titik. | Untuk menghitungnya digunakan dengan prinsip turunan pada sebuah titik. | ||
| + | |||
| + | Berikut adalah rumus deret taylor : | ||
| + | |||
| + | [[File:Taylor.PNG]] | ||
Revision as of 21:17, 9 September 2019
Nama : Rafi Ahmad Eshandra
NPM : 1706986486
Jurusan : Teknik Mesin
No HP : 082114306757
KEGIATAN DIKELAS
Selasa, 3 September 2019
PERTEMUAN 1
Metode Numerik adalah teknik yang digunakan untuk memformulasikan persoalan matematika sehingga dapat dipecahkan dengan operasi perhitungan biasa.
Pada pertemuan kali ini materi yang diberikan adalah mengenai pengolahan data dengan keterbatasan kemampuan dalam menghitung. Dimana pengaplikasian
metode numerik sangat berguna dalam kehidupan sehari-hari. Karena hasil yang didapatkan akan lebih presisi dan akurat.
Materi yang diberikan pada pertemuan kali ini adalah Metode Taylor dimana metode ini berfungsi untuk mengaproksimasikan nilai dari sebuah
fungsi.
Dalam hal ini deret tersebut merupakan jumlah tak hingga dari suku pada deret.
Untuk menghitungnya digunakan dengan prinsip turunan pada sebuah titik.
Berikut adalah rumus deret taylor :