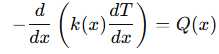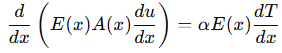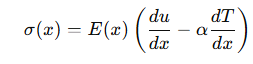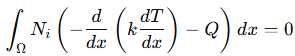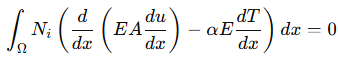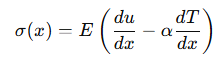Difference between revisions of "Hazimi Hamar"
Hazimihamar (talk | contribs) |
Hazimihamar (talk | contribs) |
||
| Line 277: | Line 277: | ||
'''3.''' Susun matriks kekakuan global 𝐾 structural. Terapkan syarat batas dan selesaikan 𝑢 (𝑥). | '''3.''' Susun matriks kekakuan global 𝐾 structural. Terapkan syarat batas dan selesaikan 𝑢 (𝑥). | ||
| − | Post-Processing: | + | Post-Processing: Hitung tegangan termal |
| − | |||
| − | Hitung tegangan termal | ||
[[File:Postprocessing tegangan termal.png|1100px|thumb|center]] | [[File:Postprocessing tegangan termal.png|1100px|thumb|center]] | ||
Latest revision as of 07:57, 20 November 2024
Hello, Welcome my first Home Page, in the form of assignment for meeting 1 in the Finite Element & Multhiphysics (27/08/2024)
Dalam kerangka DAI5 Framework yang merupakan konsep dari bapak Dr. Ahmad Indra berperan sebagai inisiator dalam kerangka ini, dengan pandangan filosofis yang mendasar, "I am My Consciousness." Yang dapat digunakan sebagai bentuk pemecahan masalah dan dapat menghasilkan bukti dan solusi.
1. Intention “Niat” sangat penting dalam kerangka DAI5 karena menetapkan tujuan atau hasil yang diinginkan dari proses berpikir. Hal ini selaras dengan filosofi kesadaran, di mana niat merupakan aspek kunci dari keterlibatan mental kita dengan dunia. Memahami niat membantu menjaga fokus dan kejelasan, serta mencegah gangguan, sehingga individu dapat tetap sesuai dengan nilai dan tujuan inti kita. Pemikiran yang disengaja ini menjadi dasar bagi banyak teori kognitif dan emosional, di mana kesadaran akan alasan berpikir dapat membentuk tindakan.
2. Initial Thinking “Pemikiran Awal” Tahap ini merupakan fase eksplorasi di mana individu bebas menggali dan merenungkan masalah. Ini adalah waktu untuk berasosiasi secara bebas tanpa penilaian atau batasan langsung. Pemikiran awal membantu mengenali berbagai aspek suatu masalah, mendorong peserta untuk mengandalkan intuisi dan pengalaman mereka. Tahap ini bertujuan mengumpulkan beragam perspektif sebelum beralih pada solusi yang lebih terfokus.
3. Idealization adalah tentang membayangkan skenario dan solusi terbaik yang mungkin, melampaui keterbatasan saat ini. Tahap ini mendorong berpikir kreatif dan mengajak individu untuk berpikir tanpa batas, membayangkan solusi ideal. Ini sejalan dengan konsep kesadaran yang menantang individu untuk melihat melampaui keadaan dan keterbatasan saat ini. Idealization tidak berarti mengabaikan realitas, melainkan memupuk harapan dan aspirasi untuk memotivasi tindakan lebih lanjut.
4. Instruction Set idealisme yang dikembangkan selama tahap sebelumnya ke dalam langkah-langkah yang dapat ditindaklanjuti. Hal ini penting karena solusi ideal perlu didasarkan pada kenyataan melalui implementasi praktis. Menciptakan seperangkat instruksi yang jelas dan mudah dikelola membantu individu menerjemahkan pemikiran dan aspirasi mereka ke dalam tindakan nyata, memfasilitasi kemajuan menuju tujuan mereka. Efektivitas fase ini bergantung pada kejelasan dan kelayakan langkah-langkah yang dikembangkan, yang menegaskan kembali pentingnya kesengajaan dan refleksi selama proses berlangsung.
Contents
Simple Pipe Design Modelling
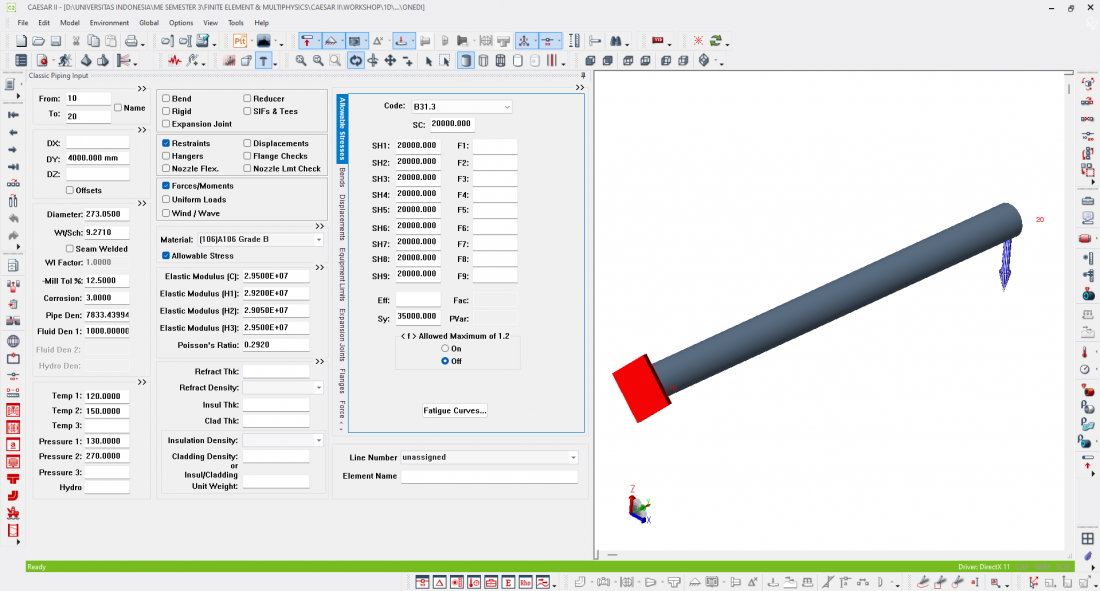
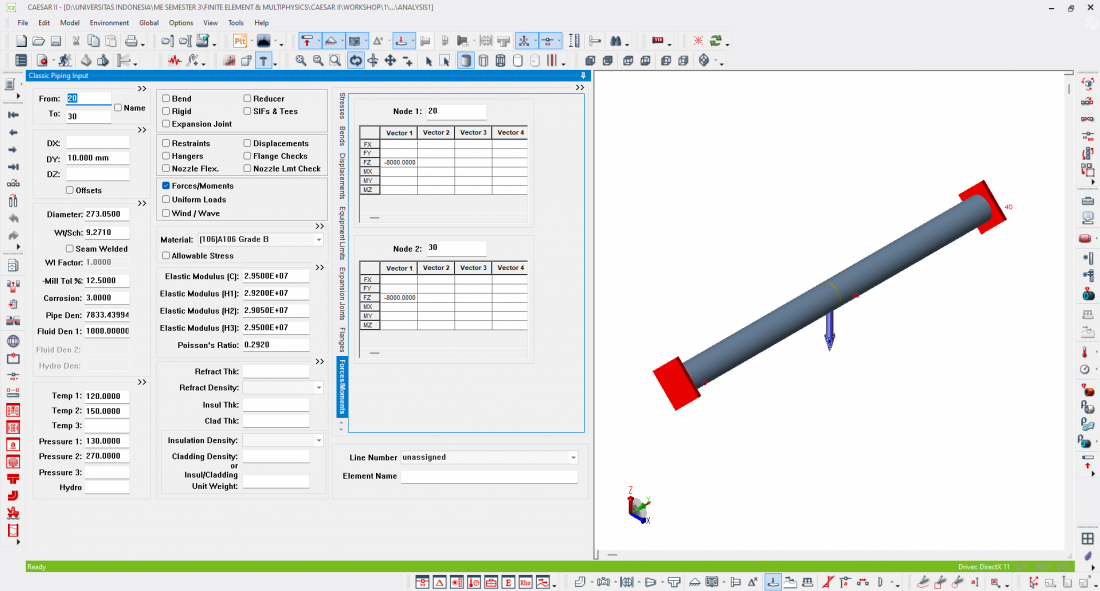
At the 4th meeting the Finite Element & Multhiphysics (4/9/2024) We do simple pipe design using Caesar II with classic piping input >> we make pipe models according to standard code B31.3 and set the layout of the pipe model including pipe length, pipe diameter, pipe wall thickness or sch, pipe fluid density, temperature and pressure are also set. At Node 10 we provide Fixed support and Node 20 we provide forces/moments in the direction of the -Z axis.
Material = ASTM 106 Grade B (Carbon Steel)
Pipe length = 4000mm = 4m
Diameter = 10in = 273.0500mm
Wallthicknes Wt/Sch = 40s = 9.2710mm
Force/Moment = 8000N
Temp Operation = 120F = 66.648,89°C
Temp Design = 150F = 83.315,56°C
Pressure Operation = 130lb./sq.in = 9139,91 kg/cm²
Pressure design = 270lb./sq.in. = 18.982,89kg/cm²
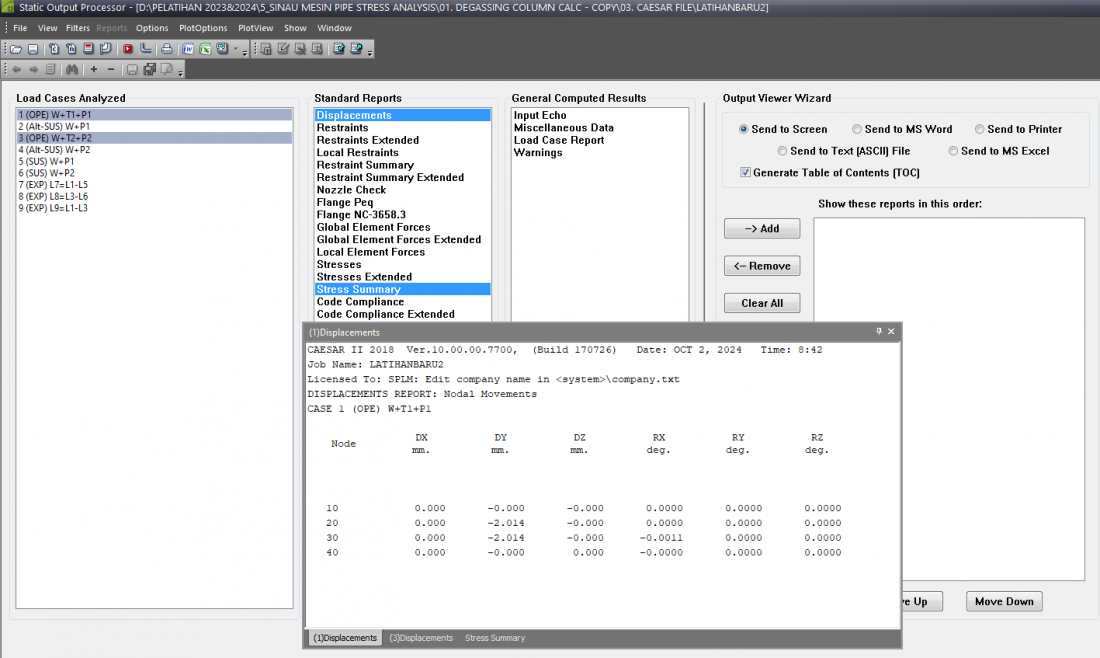
Pada parameters input pipe design yang telah kita rancang >> start run untuk statik load case dilakukan untuk crosscheck error and warnings >> Setelah running terdapat data Static Output Processor rekomendasi load cases analyzed yang diberikan oleh software pada setiap kondisi yang terdiri dari Operasi (OPE), Alternatif beban susut atau penyangga (Alt-SUS), Sustained atau penyangga yang permanen (SUS), Beban ekspansi atau thermal expansion (EXP). Dimana hasil yang diberikan tidak terdapat over stress yang terjadi pada design ini. Kita dapat melihat Stress Summary yang dihasilkan pada gambar dibawah ini.
Analisis dari model yang dirancang. Termasuk dalam pendekatan analisis 1D Bar Element, analisis seperti ini, pipa dimodelkan sebagai elemen satu dimensi (1D) yang memiliki panjang dan dapat menahan gaya aksial, tekukan, dan torsi. Analisis ini berfokus pada perilaku struktural elemen dengan asumsi bahwa gaya dan momen bekerja di sepanjang sumbu pipa. Ini adalah pendekatan yang cocok untuk memodelkan pipa panjang seperti yang ditunjukkan di gambar, di mana distribusi tegangan dan perpindahan dipertimbangkan sepanjang sumbu pipa tanpa perlu representasi penuh dalam tiga dimensi (3D). Berikut hasil dari analisis simple pipe design modelling yang terdapat pada gambar dibawah, sebagai berikut:
<<<Stress Summary Conditions:>>>
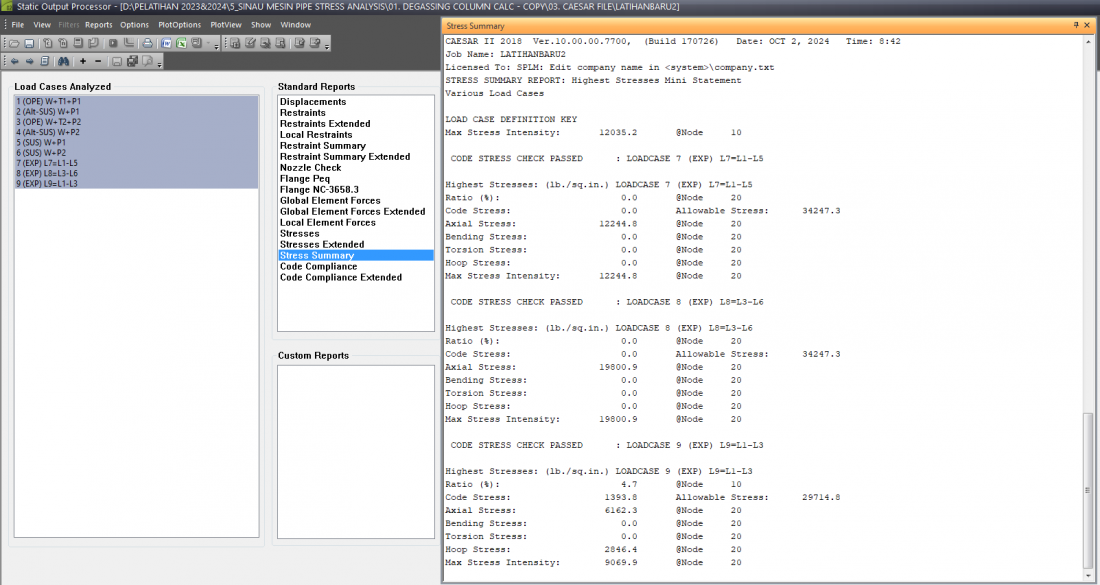
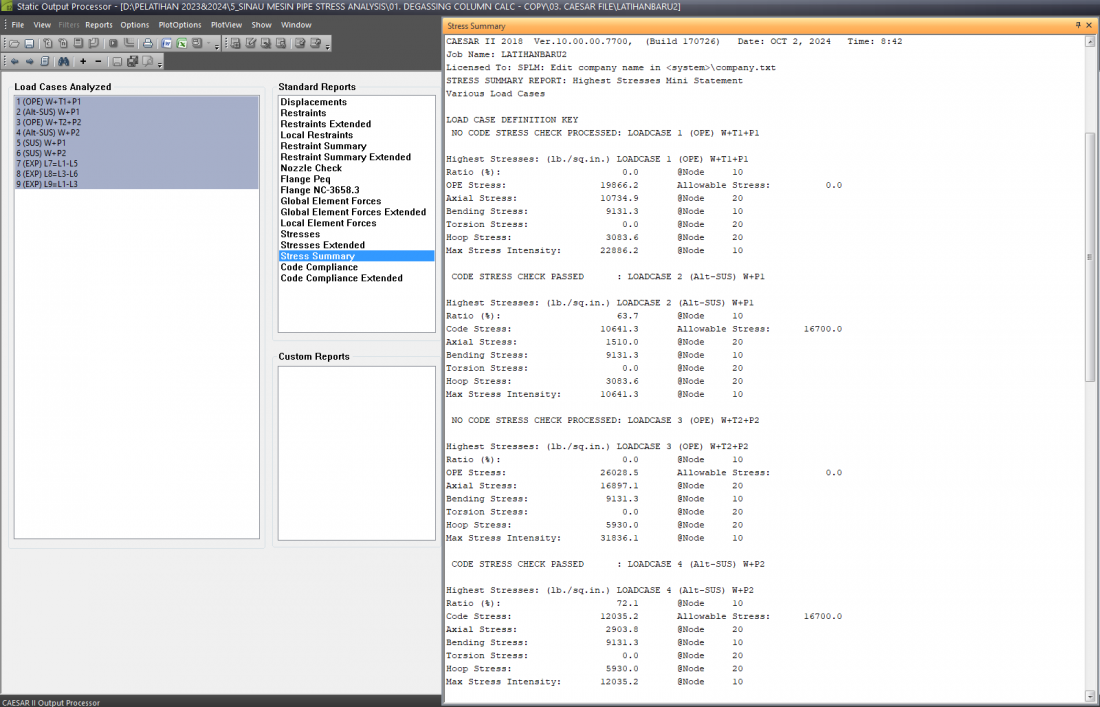
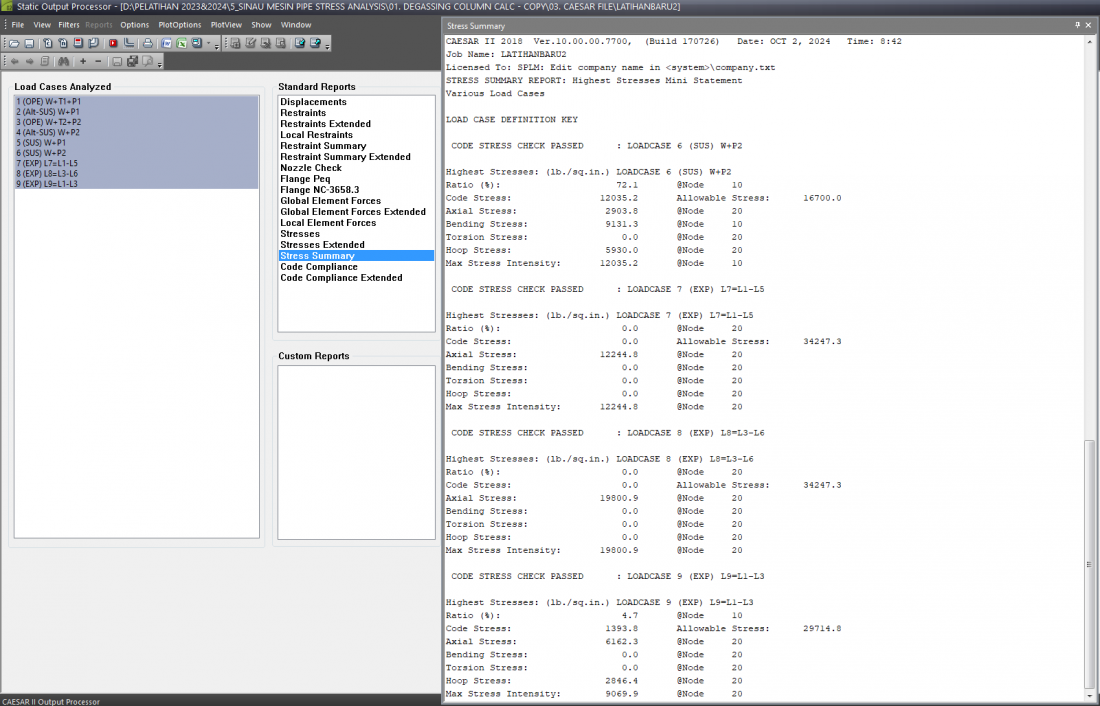
Terdapat kondisi analisis nilai tegangan (Stresses) yang diberikan oleh software dengan Allowable Stress Code B31.3. Berikut penjelasannya
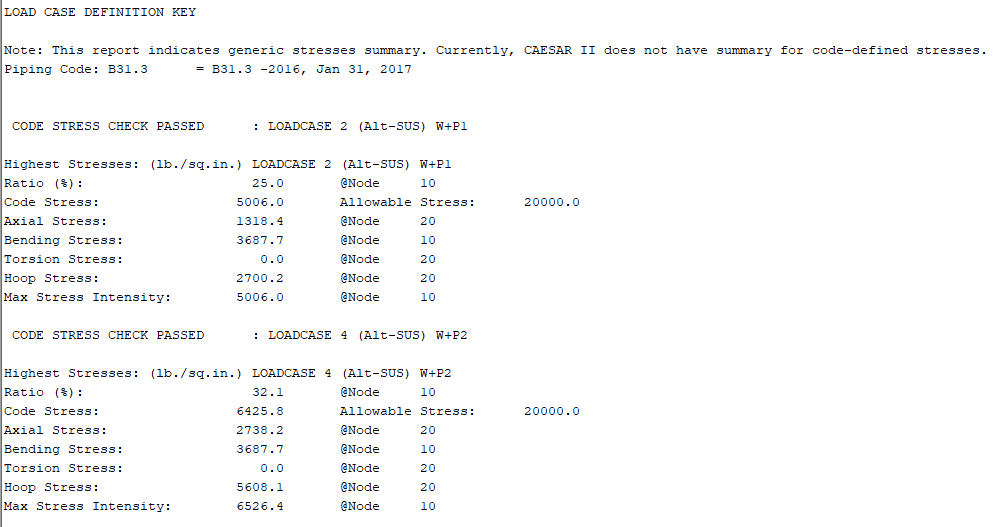
1. Loadcase 2 (Alt-SUS) W + P1 (kondisi operasi), tegangan yang dihasilkan pada node 10 adalah 5006.0 lb/sq.in. dengan rasio 25.0% dari tegangan yang diizinkan, menunjukkan bahwa kondisi beban berat dan tekanan operasi P1 masih aman di bawah batas allowable stress 20000 lb/sq.in.
2. Loadcase 4 (Alt-SUS) W + P2 (kondisi design), tegangan yang dihasilkan node 10 lebih tinggi, yaitu 6425.8 lb/sq.in., dengan rasio 32.1% dari tegangan yang diizinkan, tetapi tetap berada dalam batas aman, menandakan bahwa pipa mampu menahan beban pada tekanan desain P2 tanpa melampaui batas tegangan.
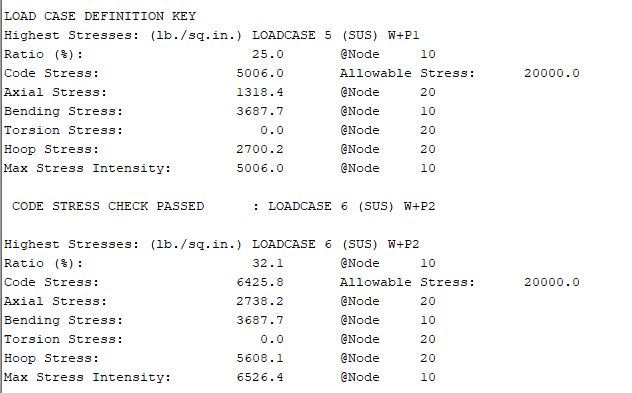
3. Loadcase 5 (SUS) W + P1, kondisi beban berat dan tekanan operasi P1 menghasilkan tegangan yang sama seperti pada Loadcase 2 (5006.0 lb/sq.in.), dengan rasio 25.0%, memastikan bahwa tekanan operasi normal P1 tidak menimbulkan tegangan berlebih pada sistem.
4. Loadcase 6 (SUS) W + P2, tegangan mencapai 6425.8 lb/sq.in., atau 32.1% dari allowable stress, yang masih dalam batas aman untuk kondisi desain dengan tekanan P2, mengindikasikan keamanan sistem terhadap kondisi susut atau penyangga dengan tekanan maksimum yang dirancang.
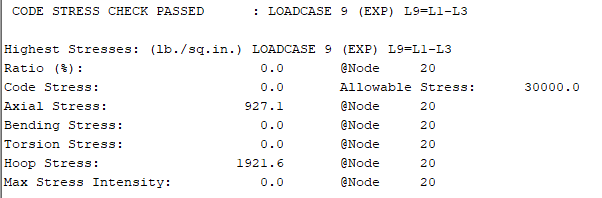
5. Loadcase 9 (EXP) L9 = L1 - L3, yang merupakan kondisi ekspansi termal antara kondisi operasi dan desain, tegangan yang dihasilkan sangat rendah (0.0% dari allowable stress), menunjukkan bahwa ekspansi termal antara suhu T1 dan T2 tidak menyebabkan tegangan yang signifikan, dan berada jauh di bawah batas allowable stress 30000 lb/sq.in., memastikan bahwa perubahan suhu tidak memberikan dampak yang membahayakan sistem pipa pada node 20.
Kesimpulan adalah Analisis ini menunjukkan bahwa sistem pipa yang kita design aman terhadap kondisi beban yang dianalisis, baik untuk kondisi operasi P1 dan P2, maupun kondisi desain yang menggunakan temperatur T2 dan tekanan P2.
<<<Displacement Conditions:>>>
Data Displacement, perpindahan maksimum terjadi di node 20 dengan nilai DY sebesar 1.303 mm dan DZ sebesar -2.590 mm, yang menunjukkan pergerakan pipa dalam arah vertikal dan longitudinal akibat beban operasional. Meskipun terjadi sedikit perpindahan dan rotasi pada node tertentu, nilai-nilai ini masih dalam batas toleransi perpipaan dan tidak mengindikasikan adanya risiko deformasi signifikan.
KESIMPULAN Berdasarkan analisis stress summary dan displacement pada desain pipa, hasil menunjukkan bahwa sistem perpipaan ini berada dalam batas aman dan sesuai standar yang ditetapkan. Dari stress summary, semua load case (termasuk kondisi beban operasi dan desain) menunjukkan tegangan yang berada di bawah allowable stress yang ditentukan oleh ASME B31.3. Tegangan tertinggi terjadi pada Loadcase 6 (SUS) dengan nilai 6425.8 lb/sq.in., yang hanya mencapai 32.1% dari batas tegangan yang diizinkan, menandakan bahwa pipa ini mampu menahan kondisi operasi dan desain tanpa risiko kegagalan material. Dan Displacement maksimum terjadi di node 20 dengan nilai DY sebesar 1.303 mm adanya pergeseran vertikal ke arah DY dan longitudinal DZ sebesar -2.590 mm.
At the 5th meeting the Finite Element & Multhiphysics (10/9/2024)
1. Apakah besar pengaruh suhu luar atau ambient temperatur terhadap struktur pipa yang dialari suhu dan pressure tinggi didalam pipa?
2. Apakah variasi ketebalan dinding pipa dapat meningkatkan keamanan dan mengurangi risiko kebocoran pada tekanan desain pipa?
1D Element Bar Analysis
Pada pertemuan ini menggunakan software calculix AbaqusCAE untuk penyelesaian kasus sederhana berupa 1D Element Bar. Menggunakan Framework DAI5 untuk menyederhanakan engineering problem dan result.
1. Intention (Niat) Maksud dan tujuan dari analisis ini adalah untuk memverifikasi respons struktur batang 1D pada kondisi beban terpusat (concentrated load), dengan memeriksa perilaku deformasi (displacement) dan tegangan (stress) yang terjadi pada kasus struktur pipa yang mengalami gaya. Dengan menggunakan data material steel dan spesifikasi geometris yang diberikan, tujuan utamanya adalah untuk mengetahui besarnya pergeseran (displacement) dan tegangan (stress) yang terjadi, serta memeriksa apakah elemen batang tetap aman dan tidak mengalami kerusakan atau kegagalan struktural.
2. Initial Thinking (Pemikiran Awal) Langkah awal untuk menentukan definisi design objek dari dimensi dan geometris. Diberikan data sebagai berikut:
A = 10e4 mm^2 (Luas penampang)
L = 1000 mm (Panjang batang)
E = 200e3 Mpa (Modulus young)
F = 10e3 N (Load concentrated force)
Diketahui bahwa elemen batang memiliki ukuran penampang lintang 𝐴 = 10e4 mm^2, panjang batang 𝐿 = 4000 mm dan gaya terpusat 𝐹 = 10e3 N, Modulus elastisitas material steel adalah 𝐸 = 200e3 MPa. Berdasarkan data ini, kita dapat mengantisipasi bahwa batang akan mengalami deformasi linier pada batas elastisitasnya karena gaya terpusat yang diterapkan. Dengan demikian, kita akan menghitung displacement dan stress pada batang. Dengan rumus:
Displacement (u): 𝑢 = FL/AE
Stress (σ): 𝜎 = F/A
Berdasarkan rumus di atas, displacement dapat dihitung berdasarkan gaya, panjang batang, luas penampang, dan modulus elastisitas. Stress dihitung dari gaya per luas penampang.
3. Idealization (Idealasi) Dalam idealisasi, kita menganggap rancangan kita mendekati dengan kondisi sebenarnya, bahwa elemen batang memiliki perilaku gaya axial atau gaya elastik linier di bawah beban yang diberikan. Diperoleh dari Intial Thinking bahwa perilaku ini dapat dilakukan dengan model 1D Bar. Setelah memperoleh model dengan membangun asumsi untuk menyederhanakan kasus, berikut:
-Material steel diaplikasikan keseluruh batang dan homogen sepanjang pipa, boundary condition fixed pada ujung batang, arah gaya bergerak lurus sejajar dengan batang sehingga terjadinya tegangan dan perpindahan yang terjadi pada satu arah terhadap sumbu X. Kita juga menganggap batang dalam kondisi mendukung hanya satu titik gaya terpusat (concentrated load) dan bebas dari faktor lainnya yang dapat mempengaruhi tegangan atau deformasi. Beban yang bekerja mensimulasikan respons statis struktur pada batang.
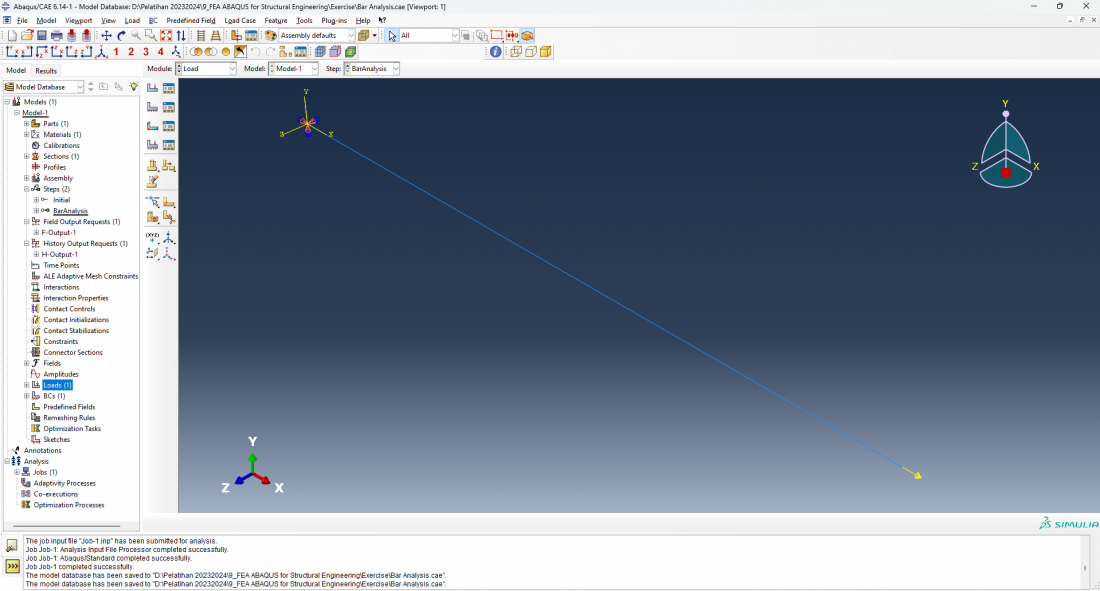
4. Instruction Set (Set Instruksi) Menentukan langkah-langkah penyelesaian yang dilakukan menggunakan software yang dipilih. Model design dibentuk menggunakan simulasi software Abaqus CAE. Tahapan ini telah disesuaikan dari Idealization yang diperoleh. Pada titik ujing garis diberikan boundary condition atau fixed support, dan ujung lainnya diberikan gaya external. Lalu Mesh dan Load diaplikasikan ke model. Terlihat pada gambar dibawah ini:
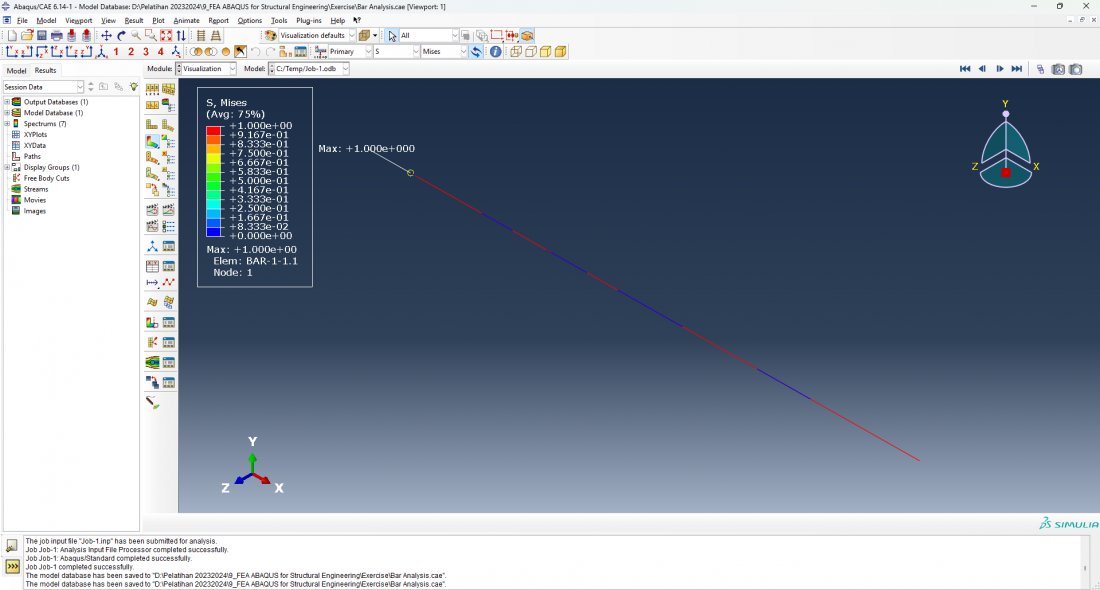
Pada implementasi parameter data yang diberikan terhadap model di AbaqusCAE, kemudian dapat kita create job untuk proses eksekusi simulasi atau analisis yang telah dibuat. Setelah model, material, dan kondisi analisis didefinisikan pada batang statis untuk running analysis Calculix. Hasil dari simulasi model yang dilakukan terlihat pada gambar dibawah ini, sebagai berikut:
Stress Mises menunjukkan seberapa besar tegangan yang dialami oleh elemen batang, dengan titik tertentu mengalami tegangan terbesar yang mungkin mendekati atau melampaui batas elastisitas material.
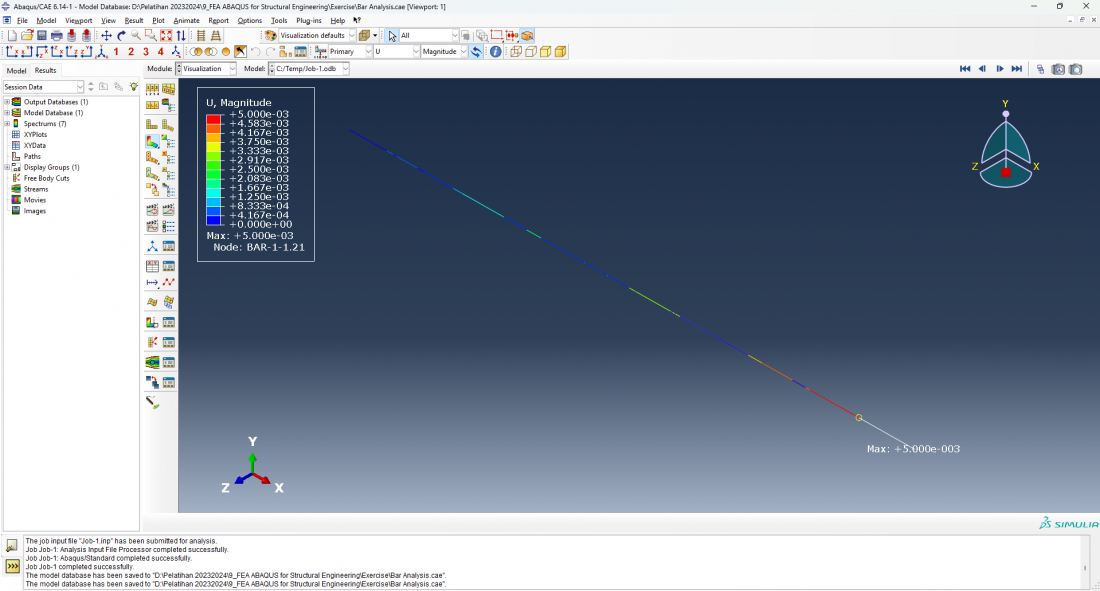
Displacement menunjukkan pergerakan elemen batang akibat gaya, dan skala warna menunjukkan besarnya perpindahan titik-titik pada elemen.
Kesimpulannya adalah Berdasarkan analisis menggunakan software Abaqus CAE pada elemen batang 1D dengan gaya terpusat, displacement (U, Magnitude) menunjukkan perpindahan maksimal sekitar 5 mm pada titik yang jauh dari tumpuan, yang masih berada dalam batas elastisitas material, menandakan batang berperilaku elastis. Sementara itu, stress (S, Mises) menunjukkan tegangan maksimum 1.000e+00 pada titik fixed, yang masih berada dalam rentang aman untuk material steel, yang memiliki kekuatan tarik lebih tinggi daripada nilai tegangan ini. Secara keseluruhan, hasil analisis ini menunjukkan bahwa batang tersebut aman dan tidak mengalami kerusakan atau deformasi permanen.
2D Element Beam Analysis
Pada pertemuan berikutnya mencoba untuk melakukan calculix use to Caesar 2019, untuk kasus sederhana. Analisis ini digunakan untuk memastikan bahwa desain pipa memenuhi persyaratan kode ASME B31.3 terhadap asumsi design yang telah kita buat. Pendekatan ini kita lakukan dengan analisis 2D Beam Element struktural. Dengan parameter sebagai berikut:
F = 8000N
Panjang Pipa = 1995 + 1995 = 4000mm
Node titik tengah sebagai tumpuan vertikal load (Force/Moment) = 10mm
dengan koefisient gesek 0.3Mu (karna Steel to Steel)
uniformload ke 2 batang pipa ke arah z 1.5lb.in dari acuan Code B31.3. Displacement dan modelling terdapat pada gambar dibawah ini:
<<<Modelling 2D Element:>>>
<<<Displacement Conditions:>>>
<<<Stress Summary:>>>
Learning Notes
Pada analisis (Finite Element Method/FEM) atau metode elemen hingga terdapat elemen 1D, elemen 2D, dan elemen 3D yang dapat digunakan untuk menyesuaikan bentuk dari kompleksitas objek sebuah bidang yang akan dianalisis. Berikut perbedaan dan penjelasan dari masing-masing elemen berdasarkan analisis multiphysiscs:
1. Elemen 1D berbentuk garis atau batang dan digunakan untuk merepresentasikan objek fisik yang memiliki satu dimensi dominan, seperti kabel, balok panjang, atau kolom. Elemen ini ideal untuk komponen yang panjang dan ramping, di mana dimensi lainnya (misalnya, lebar atau tinggi) jauh lebih kecil daripada panjangnya. Aplikasi yang biasanya digunakan untuk struktur linier seperti batang, balok, kabel, atau rangka. Elemen 1D memungkinkan analisis tegangan, deformasi, dan gaya dalam elemen tersebut. Contoh dalam Multiphysics pertama Structural Analysis yang dapat menganalisis beban dan tegangan pada balok atau batang. Kedua Thermal Analysis menganalisis distribusi suhu pada pipa panjang atau kabel listrik, di mana panas merambat sepanjang sumbu utama.
2. Elemen 2D digunakan untuk objek dengan dimensi dominan dalam dua arah (misalnya panjang dan lebar), sementara ketebalannya jauh lebih kecil atau diabaikan. Elemen ini biasanya digunakan untuk memodelkan permukaan atau pelat tipis. Aplikasi yang digunakan dalam analisis pada struktur seperti pelat, membran, atau dinding tipis di mana beban atau pengaruh fisik bekerja pada permukaan besar. Contoh dalam Multiphysics pertama Fluid-Structure Interaction dapat Memodelkan interaksi antara dinding tipis (seperti membran) dan aliran fluida di sekitarnya. Kedua Electromagnetic Analysis menganalisis arus listrik pada permukaan logam tipis, seperti dalam sirkuit. Ketiga Thermal Analysis mendistribusi suhu pada permukaan pelat logam atau dinding.
3. Elemen 3D berbentuk volumetrik, seperti tetrahedron atau hexahedron, yang mampu menangani objek tiga dimensi penuh dengan geometri kompleks. Elemen ini berguna untuk representasi detail yang mencakup seluruh volume objek dan objek yang memiliki kompleksitas geometris penuh dalam tiga dimensi. Elemen ini cocok untuk objek solid yang tidak dapat direduksi menjadi dua dimensi karena ketebalannya yang signifikan. Aplikasi yang digunakan dalam analisis struktur solid atau kompleks seperti blok, mesin, komponen mekanik besar, atau sistem yang membutuhkan pemodelan volume penuh. Contoh dalam Multiphysics pertama Thermal-Mechanical Analysis menganalisis distribusi suhu dan tegangan dalam objek solid, seperti mesin atau komponen elektronik besar. Kedua Acoustic-Vibration Analysis memodelkan respons getaran dan transmisi suara dalam objek solid seperti blok atau casing. Ketiga Fluid Flow in Porous Media menganalisis aliran fluida melalui objek solid berpori, seperti beton atau tanah.
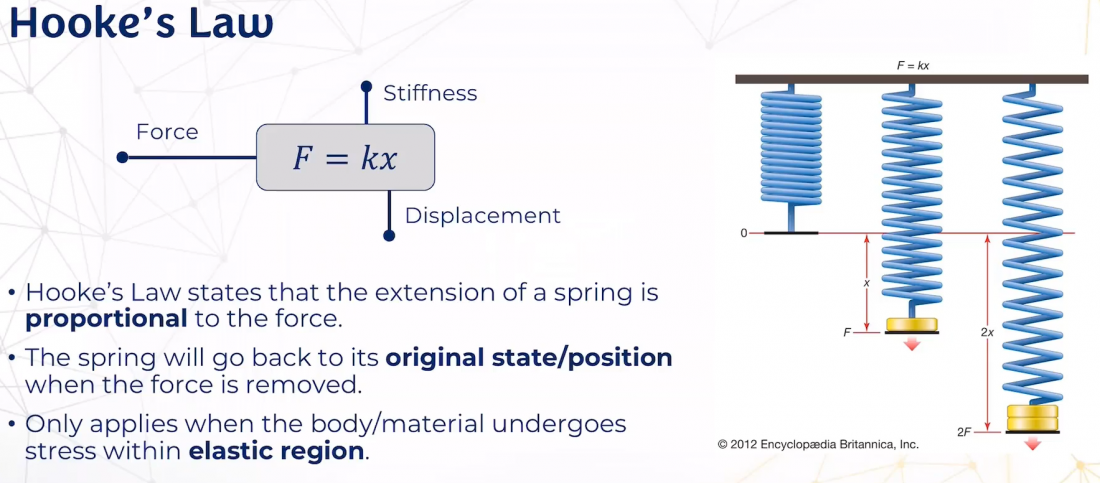
Dalam FEM (Finite Element Method), prinsip Hukum Hooke digunakan untuk menghitung tegangan (stress) dan regangan (strain) dalam elemen-elemen kecil suatu model. Hukum ini diterapkan dalam domain elastis untuk menentukan deformasi atau perpindahan elemen ketika beban diberikan, terutama dalam analisis struktur dan material elastis. Setiap elemen dalam FEM mematuhi hubungan linier antara tegangan dan regangan dalam batas elastisitas, sehingga perpindahan akibat gaya dapat dianalisis secara rinci pada level komponen. Terdapat pada gambar diatas Hukum Hooke menyatakan bahwa gaya (F) yang diterapkan pada sebuah pegas akan menghasilkan perpanjangan (x) yang sebanding, dengan persamaan 𝐹= 𝑘𝑥, di mana 𝑘 adalah kekakuan atau konstanta pegas perpanjangan pegas sebanding dengan gaya yang diterapkan padanya, selama material berada dalam batas elastis. Ini berarti semakin besar gaya, semakin besar perpanjangan yang terjadi. Kedua, ketika gaya dilepaskan, pegas atau material akan kembali ke bentuk atau posisi awalnya jika material tersebut tetap dalam wilayah elastis. Ketiga, Hukum Hooke hanya berlaku selama material berada dalam rentang elastis, di mana deformasi yang terjadi masih bisa pulih sepenuhnya tanpa perubahan permanen pada struktur material.
Stiffness (k) pada gambar ini menggambarkan kekakuan pegas, yang berperan serupa dalam elemen-elemen struktural pada model FEM.
Displacement (x) menggambarkan perubahan bentuk, yang dalam analisis FEM mengukur deformasi pada titik-titik elemen akibat gaya eksternal.
Pada FEM, prinsip dasar Hukum Hooke digunakan untuk mengembangkan matriks kekakuan yang diperlukan untuk menyelesaikan persamaan di berbagai elemen dan menggabungkannya dalam keseluruhan sistem struktur. Proporsionalitas antara Gaya dan Perpanjangan Hukum Hooke menyatakan bahwa perpanjangan pegas sebanding dengan gaya yang diterapkan, selama dalam batas elastisitas. Artinya, semakin besar gaya, semakin besar perpanjangan. Kembali ke Posisi Awal ketika gaya dilepaskan, pegas atau material akan kembali ke bentuk atau posisi aslinya, asalkan material tersebut tetap dalam wilayah elastis. Berlaku dalam Wilayah Elastis hukum ini hanya berlaku selama material atau pegas masih dalam rentang elastis, yaitu ketika deformasi masih dapat pulih sepenuhnya tanpa perubahan permanen pada struktur material.
Berikutnya pada Hukum Hooke dalam 3D untuk material elastis isotropik, yang menjelaskan hubungan antara tegangan (stress) dan regangan (strain) dalam kondisi aksial dan geser, mendefinisikan hubungan linier antara tegangan dan regangan pada material elastis isotropik (material yang sifatnya sama dalam semua arah). Dalam konteks 3D, hukum ini memerlukan konstanta elastisitas material, yaitu Modulus Young (E) dan Rasio Poisson (ν), serta Modulus Geser (G), yang digunakan dalam persamaan tegangan dan regangan. Berikut penjelasan dari bagian-bagian tersebut:
Axial Strain Regangan aksial (ε) pada arah x, y, dan z dihitung dari tegangan pada ketiga sumbu ini serta efek dari Rasio Poisson, yang menghubungkan tegangan di satu arah dengan perubahan bentuk di arah yang lain.
Shear Strain Regangan geser (γ) pada bidang xy, zx, dan yz berhubungan langsung dengan tegangan geser pada bidang yang sama dan Modulus Geser G. Shear strain menunjukkan distorsi atau perubahan bentuk pada bidang tertentu akibat tegangan geser.
Axial Stress Tegangan aksial (σ) pada arah x, y, dan z diperoleh dengan mengalikan Modulus Young (E), Rasio Poisson (ν), dan regangan aksial pada ketiga arah. Rumus ini menggabungkan pengaruh regangan dari semua arah, yang menunjukkan sifat isotropik dari material tersebut.
Shear Stress Tegangan geser (τ) pada bidang xy, yz, dan zx berkaitan langsung dengan shear strain pada bidang yang sama dan Modulus Geser (G). Shear stress ini menunjukkan tegangan yang menyebabkan distorsi di bidang tertentu.
Diagram Kubus di tengah gambar mengilustrasikan tegangan pada berbagai arah pada suatu elemen kubus material. Arah tegangan aksial (σ_x, σ_y, σ_z) ditunjukkan di sepanjang sumbu utama x, y, dan z, sementara tegangan geser (τ_xy, τ_yz, τ_zx) ditunjukkan pada bidang antar-sumbu. Diagram ini membantu memvisualisasikan bagaimana tegangan bekerja pada elemen dalam ruang tiga dimensi. Transformasi Stress and Strain persamaan pada gambar menunjukkan bahwa tegangan dan regangan saling berhubungan melalui transformasi berdasarkan Hukum Hooke dalam 3D. Transformasi ini memperhitungkan pengaruh dari semua komponen tegangan pada regangan aksial dan pengaruh regangan pada tegangan aksial, mencerminkan sifat mekanik material isotropik.
1D Multiphysics Analysis: Heat Conduction and Thermal Stress Using Finite Element Method
Berikut adalah langkah-langkah mendetail berdasarkan kerangka kerja DAI5 untuk menurunkan dan mengimplementasikan Metode Elemen Hingga (FEM) untuk masalah 1D multiphysics (termal dan struktural):
1. Initiator
Kutipan dari Dr. Ahmad Indra: "Saya adalah kesadaran saya." Pernyataan ini menggaris bawahi pentingnya kesadaran untuk memahami proses analisis secara mendalam, sehingga setiap langkah analisis FEM menjadi jelas dan dapat diterapkan.
2. Intention (Niat)
Tujuannya memahami pemecahan masalah teknik menggunakan pendekatan sistematis dan terstruktur. Dalam analisis ini, kita berfokus pada pemodelan multiphysics 1D yang melibatkan konduksi panas dan deformasi mekanik akibat ekspansi termal, relevan dalam aplikasi teknik mesin seperti desain material pada pipa atau pembangkit listrik. Kita ingin memodelkan dan menganalisis masalah konduksi panas 1D dengan efek ekspansi termal yang menghasilkan deformasi mekanik. Fokus utama adalah menghitung distribusi temperatur dan tegangan termal (thermal stress).
3. Initial Thinking (Pemikiran Awal)
Penyusunan Masalah: Menganalisis distribusi temperatur 𝑇 (𝑥), deformasi mekanik 𝑢 (𝑥), dan tegangan termal 𝜎 (𝑥) dalam sistem 1D menggunakan metode elemen hingga (FEM).
Tujuan: Memahami interaksi antara fenomena termal dan mekanik dalam suatu domain 1D.
Aplikasi: Analisis ini penting dalam desain pipa, material pengangkut panas, dan komponen struktur yang mengalami beban termal.
Fenomena yang terlibat:
- Termal (Konduksi panas):
di mana 𝑇 adalah temperatur, 𝑘(𝑥)adalah konduktivitas termal, dan 𝑄(𝑥) adalah sumber panas.
- Struktural (Deformasi mekanik):
di mana 𝑢 adalah perpindahan, 𝐸(𝑥) adalah modulus elastisitas, 𝐴(𝑥) adalah luas penampang, dan 𝛼 adalah koefisien ekspansi termal.
Batasan (Boundary Conditions):
Temperatur tetap di kedua ujung domain:
Tujuan akhir:
Hitung distribusi 𝑇(𝑥) menggunakan persamaan konduksi panas. Gunakan 𝑇 (𝑥) untuk menghitung distribusi tegangan termal 𝜎 (𝑥) sebagai:
4. Idealization (Idealisasi)
Diskretisasi Domain
- Membagi domain [0,L] menjadi 𝑛 elemen kecil, dengan simpul pada setiap ujung elemen.
- Temperatur T(x) dan perpindahan u(x) diaproksimasi menggunakan fungsi interpolasi linier
Formulasi FEM menggunakan Weighted Residual Method (WRM):
Konduksi panas: Menggunakan metode Galerkin:
Setelah integrasi by parts, persamaan menjadi: 𝐾 thermal 𝑇 = 𝐹 thermal
Deformasi mekanik: Menggunakan metode Galerkin:
Proses yang sama diterapkan: 𝐾 structural 𝑢 = 𝐹 structural
Asumsi:
- Material homogen dalam elemen. - Linear shape functions 𝑁𝑖 (𝑥) untuk setiap elemen. - Kondisi steady state
5. Instruction Set (Set Instruksi)
Algoritma Penyelesaian:
1. Termal Problem: Diskritisasi domain. Hitung elemen stiffness 𝐾 𝑒 thermal dan vektor beban 𝐹 𝑒 thermal. Susun matriks kekakuan global 𝐾 thermal. Terapkan syarat batas dan selesaikan 𝑇 (𝑥).
2. Struktural Problem: Hitung elemen stiffness 𝐾 𝑒 structural dan vektor beban 𝐹 𝑒 structural menggunakan gradien 𝑇 (𝑥).
3. Susun matriks kekakuan global 𝐾 structural. Terapkan syarat batas dan selesaikan 𝑢 (𝑥).
Post-Processing: Hitung tegangan termal
Post-processing tegangan termal menghubungkan fenomena mekanik dan termal dengan cara menghitung kontribusi strain termal ( 𝛼 𝑑𝑇/𝑑𝑥 ) dan strain mekanik ( 𝑑𝑢/𝑑𝑥 ) untuk mendapatkan distribusi tegangan total (𝜎 (𝑥)). Langkah ini sangat penting untuk mengevaluasi kinerja material di bawah kondisi operasi tertentu.
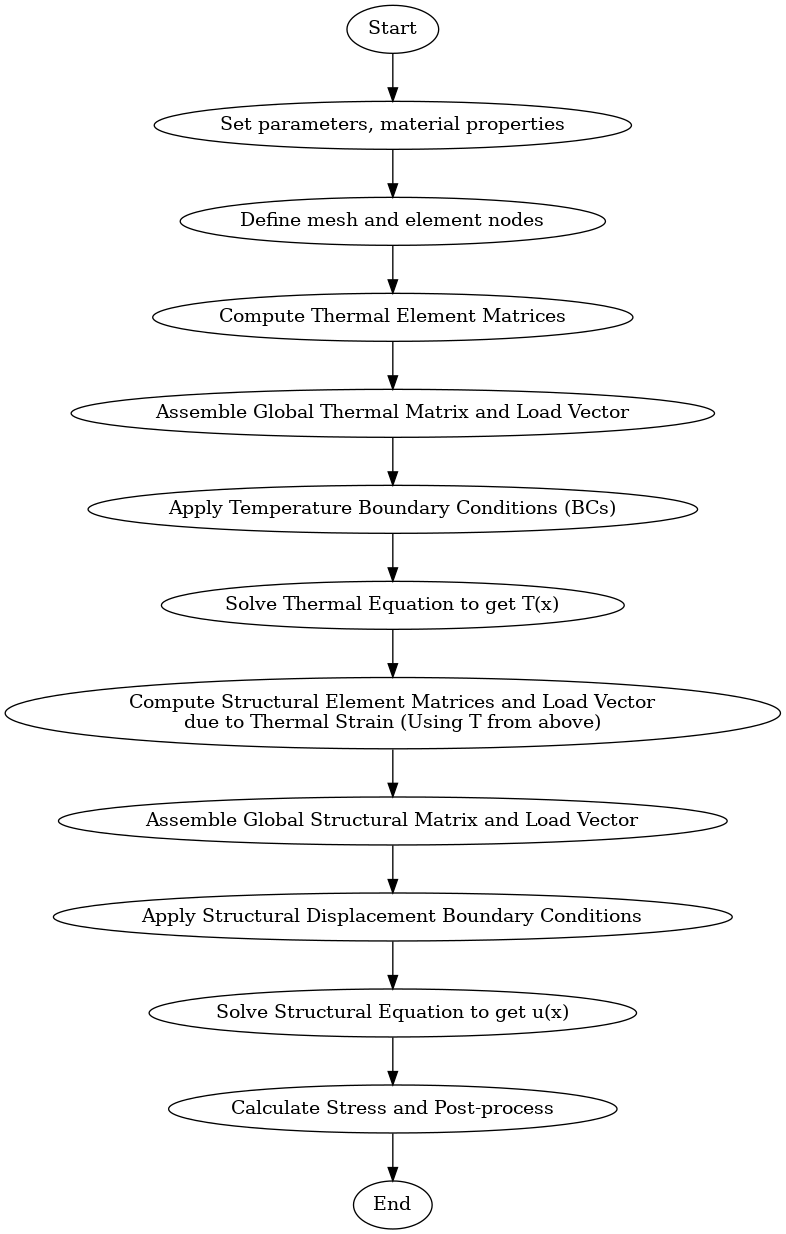
Flowchart
Code Python run with Google Collab to calculate the Temperature Distribution, Displacement Distribution and Thermal Stress Distribution of a 1D pipe. This code also illustrates how continuous real-time feedback (simulated here) could be integrated into a DAI5 framework. We’ll calculate these values and display them over a range of forces to simulate "conscious continuum" monitoring.
# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
# Parameters
n_elements = 10
L = 1.0
k = 1.0 # Thermal conductivity
E = 200e9 # Young's modulus
A = 1e-4 # Cross-sectional area
alpha = 1e-5 # Thermal expansion coefficient
Q = 1e3 # Heat source
T0, TL = 100, 50 # Boundary temperatures
# Mesh
nodes = np.linspace(0, L, n_elements + 1)
dx = nodes[1] - nodes[0]
# Initialize matrices
K_thermal = np.zeros((n_elements + 1, n_elements + 1))
F_thermal = np.zeros(n_elements + 1)
K_structural = np.zeros((n_elements + 1, n_elements + 1))
F_structural = np.zeros(n_elements + 1)
# Thermal problem
for e in range(n_elements):
k_local = (k / dx) * np.array([[1, -1], [-1, 1]])
f_local = (Q * dx / 2) * np.array([1, 1])
K_thermal[e:e+2, e:e+2] += k_local
F_thermal[e:e+2] += f_local
K_thermal[0, 0] = K_thermal[-1, -1] = 1
F_thermal[0], F_thermal[-1] = T0, TL
T = np.linalg.solve(K_thermal, F_thermal)
# Structural problem
for e in range(n_elements):
dT_dx = (T[e+1] - T[e]) / dx
k_local = (E * A / dx) * np.array([[1, -1], [-1, 1]])
f_local = (alpha * E * dT_dx * dx / 2) * np.array([1, 1])
K_structural[e:e+2, e:e+2] += k_local
F_structural[e:e+2] += f_local
K_structural[0, 0] = 1
F_structural[0] = 0
u = np.linalg.solve(K_structural, F_structural)
# Thermal stress
sigma = np.zeros(n_elements)
for e in range(n_elements):
du_dx = (u[e+1] - u[e]) / dx
dT_dx = (T[e+1] - T[e]) / dx
sigma[e] = E * (du_dx - alpha * dT_dx)
# Plot results
plt.figure(figsize=(12, 6))
plt.subplot(3, 1, 1)
plt.plot(nodes, T, '-o', label="Temperature")
plt.title("Temperature Distribution")
plt.subplot(3, 1, 2)
plt.plot(nodes, u, '-o', label="Displacement")
plt.title("Displacement Distribution")
plt.subplot(3, 1, 3)
plt.plot(nodes[:-1] + dx / 2, sigma, '-o', label="Stress")
plt.title("Thermal Stress Distribution")
plt.tight_layout()
plt.show()
Kode ini menyelesaikan distribusi temperatur, perpindahan mekanik, dan tegangan termal dalam domain 1D menggunakan FEM. Setiap bagian kode mencerminkan langkah-langkah algoritma dalam DAI5 Framework, memastikan pendekatan analitis yang logis dan terstruktur.
Setelah mendapatkan contoh program dari ChatGPT, code dicoba menggunakan Google Colabs, berikut hasil yang diberikan :
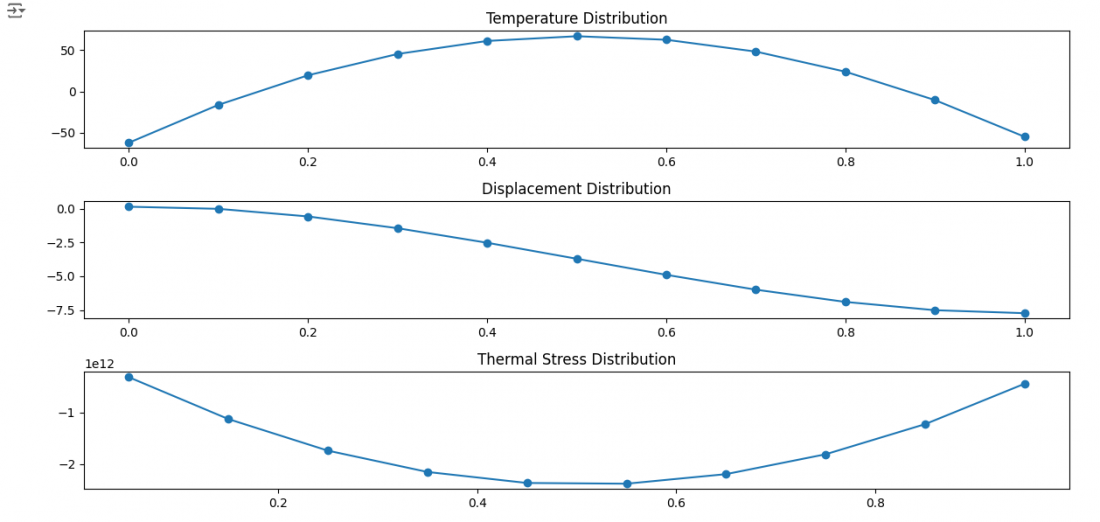
Berikut penjelasan diagram adalah :
1. Temperature Distribution Grafik distribusi temperatur menggambarkan bagaimana temperatur 𝑇(𝑥) berubah sepanjang domain. Dari grafik, temperatur mulai dari nilai 𝑇(0) = −50 di ujung kiri, meningkat secara bertahap hingga mencapai puncak sekitar titik tengah domain, kemudian menurun kembali ke 𝑇 (1) = − 50 di ujung kanan. Bentuk parabola ini menunjukkan distribusi panas yang simetris, yang dihasilkan oleh sumber panas 𝑄 (𝑥) di tengah domain dan kondisi steady-state dari sistem. Gradien temperatur ( 𝑑𝑇/𝑑𝑥 ) terbesar berada di dekat ujung-ujung domain, yang memengaruhi deformasi mekanik dan tegangan termal.
2. Displacement Distribution Distribusi perpindahan 𝑢 (𝑥) menggambarkan deformasi mekanik akibat ekspansi termal dalam material. Grafik menunjukkan perpindahan menurun dari nilai 𝑢 (0) = 0 di ujung kiri, yang terfiksasi (boundary condition), hingga mencapai nilai negatif maksimum di ujung kanan. Nilai negatif perpindahan menunjukkan bahwa material mengalami kompresi, atau penyusutan panjang. Perpindahan terbesar terjadi di ujung domain, di mana gradien temperatur juga tinggi. Gradien perpindahan (𝑑𝑢/𝑑𝑥) memberikan informasi tentang strain mekanik, yang akan digunakan untuk menghitung tegangan termal.
3. Thermal Stress Distribution Distribusi tegangan termal 𝜎(𝑥) menunjukkan bagaimana tegangan berkembang sepanjang domain akibat kombinasi gradien temperatur (𝑑𝑇/𝑑𝑥) dan gradien perpindahan (𝑑𝑢/𝑑𝑥). Grafik menunjukkan tegangan termal mencapai nilai negatif maksimum (kompresi) di kedua ujung domain, dengan nilai lebih kecil di tengah domain. Hal ini konsisten dengan gradien temperatur yang tinggi di dekat ujung domain. Tegangan negatif menunjukkan tekanan kompresi, yang terjadi ketika material mencoba menyusut akibat gradien temperatur tetapi terhambat oleh kondisi mekanik material. Jika tegangan ini melampaui batas elastis material, deformasi plastis atau kegagalan material dapat terjadi.
Kesimpulan Dari analisis distribusi temperatur, perpindahan, dan tegangan termal, dapat disimpulkan bahwa:
Interaksi termal dan mekanik dalam domain material menunjukkan bahwa gradien temperatur langsung memengaruhi gradien perpindahan, yang pada akhirnya menentukan distribusi tegangan termal. Area kritis berada di ujung domain, di mana gradien temperatur dan tegangan termal mencapai nilai maksimum. Ini menunjukkan potensi risiko kegagalan material di area tersebut, terutama di bawah kondisi operasi ekstrem. Distribusi yang diperoleh (parabola untuk temperatur, linier untuk perpindahan, dan simetris untuk tegangan) konsisten dengan solusi teoretis sistem 1D dalam kondisi steady-state. Analisis ini dapat digunakan untuk mengevaluasi desain material yang terpapar perubahan suhu dan memitigasi kegagalan struktural dengan meminimalkan gradien temperatur atau memilih material dengan sifat elastisitas dan ekspansi termal yang sesuai. Hasil ini memberikan wawasan penting untuk desain dan evaluasi material teknik mesin yang beroperasi di bawah kondisi termal.