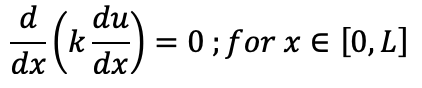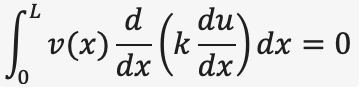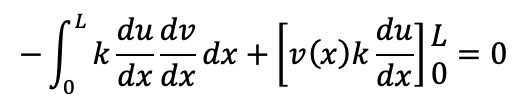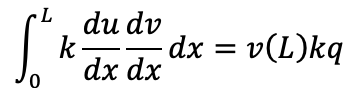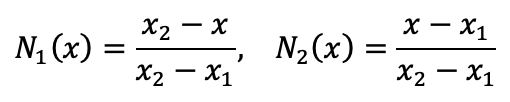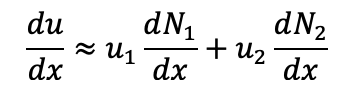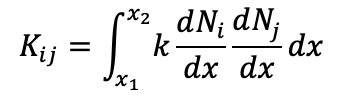Difference between revisions of "User:Muhamad.akbar41"
| Line 213: | Line 213: | ||
# Parameters | # Parameters | ||
| − | L = 10.0 # Length of the rod | + | L = 10.0 # Length of the rod |
| − | N = 5 # Number of elements | + | N = 5 # Number of elements |
| − | k = 1.0 # Thermal conductivity | + | k = 1.0 # Thermal conductivity |
| − | f = 2.0 # Heat source term | + | f = 2.0 # Heat source term |
| − | u_0 = 0.0 # Dirichlet BC at x=0 | + | u_0 = 0.0 # Dirichlet BC at x=0 |
| − | q_L = -5.0 # Neumann BC at x=L | + | q_L = -5.0 # Neumann BC at x=L |
# Mesh generation | # Mesh generation | ||
| − | nodes = np.linspace(0, L, N + 1) # Node positions | + | nodes = np.linspace(0, L, N + 1) # Node positions |
| − | h = L / N # Element length | + | h = L / N # Element length |
# Initialize global stiffness matrix and force vector | # Initialize global stiffness matrix and force vector | ||
| − | K = np.zeros((N + 1, N + 1)) | + | K = np.zeros((N + 1, N + 1)) |
| − | F = np.zeros(N + 1) | + | F = np.zeros(N + 1) |
# Assembly process | # Assembly process | ||
| − | for e in range(N): | + | for e in range(N): |
| − | + | # Element stiffness matrix for element e | |
| − | + | Ke = (k / h) * np.array([[1, -1], [-1, 1]]) | |
| − | + | # Element force vector for element e (assuming f(x) constant) | |
| − | + | Fe = (f * h / 2) * np.array([1, 1]) | |
| − | + | # Assemble into global matrix | |
| − | + | K[e:e+2, e:e+2] += Ke | |
| − | + | F[e:e+2] += Fe | |
# Apply boundary conditions | # Apply boundary conditions | ||
# Dirichlet BC at x=0 | # Dirichlet BC at x=0 | ||
| − | K[0, :] = 0 | + | K[0, :] = 0 |
| − | K[0, 0] = 1 | + | K[0, 0] = 1 |
| − | F[0] = u_0 | + | F[0] = u_0 |
# Neumann BC at x=L | # Neumann BC at x=L | ||
| − | F[-1] += q_L | + | F[-1] += q_L |
# Solve for nodal temperatures | # Solve for nodal temperatures | ||
| − | U = np.linalg.solve(K, F) | + | U = np.linalg.solve(K, F) |
# Plot results | # Plot results | ||
| − | plt.plot(nodes, U, '-o', label="Temperature Distribution") | + | plt.plot(nodes, U, '-o', label="Temperature Distribution") |
| − | plt.xlabel("Position x") | + | plt.xlabel("Position x") |
| − | plt.ylabel("Temperature u(x)") | + | plt.ylabel("Temperature u(x)") |
| − | plt.title("1D FEM Solution of Heat Conduction") | + | plt.title("1D FEM Solution of Heat Conduction") |
| − | plt.legend() | + | plt.legend() |
| − | plt.grid() | + | plt.grid() |
| − | plt.show() | + | plt.show() |
``` | ``` | ||
Revision as of 09:44, 19 November 2024
Nama saya Muhamad Akbar Fuad, nama panggilan Akbar. Saya adalah seorang mantan kepala produksi di sebuah perusahaan manufaktur elektronika di Kota Bogor. Alhamdulillah, saat ini sudah menemukan pekerjaan baru sebagai guru matematika sma. Bidang peminatan yang diambil adalah Sistem Otomasi dan Manufaktur, dengan topik penelitian Additive Manufacturing Systems. Saya memiliki interest akan suatu sistem produksi massal. Didorong dengan pengalaman
1. Menjalankan Mesin-Mesin Produksi 2. Manajemen Inventory Perusahaan
sebagai seorang kepala produksi membuat pemikiran terbaru untuk mengoptimalkan kehandalan Produksi dan Manajerial Keuangan Perusahaan. Pengalaman bekerja selama 1,5 tahun ,ternyata, membuka realitas hidup bahwa PHK itu TIDAK LEPAS dari resiko-resiko yang mungkin dialami oleh masing-masing pegawai perusahaan. Oleh karenanya, tujuan utama mengapa saya mempelajari materi Komputasi Teknik adalah untuk
1. mengoptimalkan ketahanan produksi unit usaha 2. mencegah angka PHK yang lebih meluas lagi
ditengah ketidakpastikan ekonomi global dan kondisi perpolitikan nasional.
Diharapkan, ilmu-ilmu tentang komputasi teknik yang akan saya pelajari mampu membawa angin segar untuk perusahaan-perusahaan lainnya dalam mempertahankan usahanya dan meminimalisir angka PHK ditengah ketidakpastian ekonomi saat ini. Cukuplah hanya saya yang di rumahkan, saya hanya tidak ingin melihat angka PHK kembali meningkat.
BELAJAR KOMPUTASI TEKNIK DENGAN CHAT GPT
DAI5
Conscious Thinking (Think about Reality and How to Solve it all)
I(2) Intention I(3) Initial Thinking I(4) Idealization I(5) Instruction Set
JILID 1 : 1-Dimensional Partial Differential Equation (PDE)
Question 1: Did you know about DAI5?
The DAI5 Framework is a structured method designed to support systematic problem-solving, particularly in engineering and technical analysis. Developed by Dr. Ahmad Indra Siswantara, the DAI5 framework consists of five main steps: defining the problem, analyzing causes, ideating solutions, implementing, and evaluating outcomes. This approach is often applied in complex scenarios like numerical simulations, finite element analysis, and stress testing within engineering fields. By using DAI5, users aim to ensure each phase is rigorously analyzed to optimize solutions and outcomes, as demonstrated in various technical case studies on topics such as fluid dynamics and pipe stress analysis.
Question 2: Can you derive finite element equations from 1D PDE governing equations using weighted residual in a very simple way along with an example?
Certainly! Deriving the finite element equations from a 1D partial differential equation (PDE) using the weighted residual method is a great way to understand the basics of the finite element method (FEM). Let’s go through it step-by-step with a simple example.
Problem Setup: 1D PDE Example Consider the 1D steady-state heat conduction equation with no internal heat generation:
where:
• u(x) is the temperature field, • k is the thermal conductivity (assumed constant for simplicity), • L is the length of the domain.
Suppose we have the boundary conditions:
1. u(0)=u0 (a Dirichlet boundary condition), 2. du/dx = q at x = L (a Neumann boundary condition).
Step 1: Formulate the Weak Form (Weighted Residual Form) To derive the finite element equations, we start with the weak form of the governing equation. This involves:
1. Multiplying the differential equation by a test function v(x), 2. Integrating over the domain, 3. Applying PARTIAL INTEGRATION to reduce the order of derivatives on u.
The weighted residual form is:
Using integration by parts to move the derivative from u to v, we get:
The boundary term,[v(x).k.du/dx]L0 , will incorporate boundary conditions:
• At x=0, v(0)=0 due to the Dirichlet boundary condition (since u(0)=u0 is known). • At x=L, we have the Neumann boundary condition du/dx=q.
This leaves us with:
Step 2: Discretize the Domain and Approximate u(x) Now, we approximate u(x) using finite element shape functions. Suppose we divide the domain into two linear elements, and approximate u(x) as:
u(x) = u1.N1 (x) + u2.N2 (x)
where:
• N1(x) and N2(x) are linear shape functions, • u1 and u2 are the nodal values of u at nodes 1 and 2.
For a linear element over a small interval [x1,x2], the shape functions can be written as:
Step 3: Apply the Weighted Residual Method to Each Element For each element, we substitute the approximated u(x) and v(x) (chosen as the shape functions) into the weak form.
1. Evaluate the integrals: Substitute
2. Compute the stiffness matrix entries for each element:
For a linear element, this integral simplifies to a constant and can be calculated based on the properties of the shape functions.
3. Assemble the Global System of Equations: After computing K for each element, assemble them into a global stiffness matrix.
4. Apply Boundary Conditions to solve for the unknown nodal values.
Summary
This procedure gives you a system of linear equations:where: • K is the global stiffness matrix, • U is the vector of unknown nodal values, • F is the force vector, which includes contributions from the Neumann boundary condition.
JILID 2 : Pembuatan Kode Python
Question 3: Can you provide with algorithm, flow chart and python code?
Certainly! Here’s how you can implement the finite element method (FEM) for a 1D heat conduction problem step-by-step, including the algorithm, flowchart, and a sample Python code.
- Algorithm for 1D FEM Heat Conduction Problem
The basic steps are as follows:
1. **Input Parameters**: Set up the problem's physical and numerical parameters, such as length of the domain \( L \), number of elements \( N \), conductivity \( k \), source term \( f(x) \), and boundary conditions.
2. **Mesh Generation**: Divide the domain into \( N \) elements. Each element will have two nodes.
3. **Define Shape Functions**: For a linear 1D element, define shape functions \( N_1(x) \) and \( N_2(x) \) and their derivatives.
4. **Element Stiffness Matrix and Force Vector**:
- For each element, compute the element stiffness matrix \( \mathbf{K}^{(e)} \) and force vector \( \mathbf{F}^{(e)} \) using integration.
- Assemble the element matrices and vectors into the global stiffness matrix \( \mathbf{K} \) and global force vector \( \mathbf{F} \).
5. **Apply Boundary Conditions**:
- Modify \( \mathbf{K} \) and \( \mathbf{F} \) to incorporate boundary conditions.
6. **Solve the System of Equations**:
- Solve \( \mathbf{K} \mathbf{U} = \mathbf{F} \) for the nodal temperatures \( \mathbf{U} \).
7. **Post-process**:
- Compute temperature at each node and optionally evaluate gradients or flux.
- Flowchart for 1D FEM Heat Conduction Problem
```plaintext
+------------------------+
| Start |
+------------------------+
|
v
+------------------------+
| Input parameters |
| (L, N, k, f(x), etc.) |
+------------------------+
|
v
+------------------------+
| Mesh generation |
| Divide domain into N |
| elements, calculate |
| node positions |
+------------------------+
|
v
+------------------------+
| Initialize global |
| stiffness matrix K |
| and force vector F |
+------------------------+
|
v
+------------------------+
| For each element e: |
| - Compute element |
| stiffness matrix |
| - Compute element |
| force vector |
| - Assemble into |
| global K and F |
+------------------------+
|
v
+------------------------+
| Apply boundary |
| conditions |
+------------------------+
|
v
+------------------------+
| Solve KU = F for U |
+------------------------+
|
v
+------------------------+
| Post-process results |
| (e.g., plot temperature|
| distribution) |
+------------------------+
|
v
+------------------------+
| End |
+------------------------+
```
- Python Code for 1D FEM Heat Conduction Problem
Here’s a simple Python script that implements the FEM for a 1D heat conduction problem.
```python import numpy as np import matplotlib.pyplot as plt
- Parameters
L = 10.0 # Length of the rod N = 5 # Number of elements k = 1.0 # Thermal conductivity f = 2.0 # Heat source term u_0 = 0.0 # Dirichlet BC at x=0 q_L = -5.0 # Neumann BC at x=L
- Mesh generation
nodes = np.linspace(0, L, N + 1) # Node positions h = L / N # Element length
- Initialize global stiffness matrix and force vector
K = np.zeros((N + 1, N + 1)) F = np.zeros(N + 1)
- Assembly process
for e in range(N):
# Element stiffness matrix for element e
Ke = (k / h) * np.array([[1, -1], [-1, 1]])
# Element force vector for element e (assuming f(x) constant)
Fe = (f * h / 2) * np.array([1, 1])
# Assemble into global matrix
K[e:e+2, e:e+2] += Ke
F[e:e+2] += Fe
- Apply boundary conditions
- Dirichlet BC at x=0
K[0, :] = 0 K[0, 0] = 1 F[0] = u_0
- Neumann BC at x=L
F[-1] += q_L
- Solve for nodal temperatures
U = np.linalg.solve(K, F)
- Plot results
plt.plot(nodes, U, '-o', label="Temperature Distribution")
plt.xlabel("Position x")
plt.ylabel("Temperature u(x)")
plt.title("1D FEM Solution of Heat Conduction")
plt.legend()
plt.grid()
plt.show()
```
- Explanation of the Code
1. **Parameters**: We define the length \( L \), number of elements \( N \), thermal conductivity \( k \), heat source \( f \), and boundary conditions.
2. **Mesh Generation**: We create nodes evenly spaced along \( [0, L] \).
3. **Global Matrix and Vector Initialization**: We initialize the global stiffness matrix \( K \) and force vector \( F \).
4. **Element Stiffness Matrix and Force Vector Calculation**: For each element:
- Compute the element stiffness matrix \( \mathbf{K}^{(e)} \) using the formula for a 1D linear element.
- Compute the element force vector \( \mathbf{F}^{(e)} \) for a constant source term.
5. **Assembly**: The element matrices and vectors are added to the global matrix and vector.
6. **Boundary Conditions**:
- Apply the Dirichlet boundary condition by modifying the first row. - Apply the Neumann condition by adding to the last entry in \( F \).
7. **Solve the System**: Use `np.linalg.solve` to get the temperature distribution at the nodes.
8. **Plot**: Display the temperature distribution along the rod.
This script provides a basic approach to solving a 1D FEM problem. Let me know if you need further modifications or explanations!