Difference between revisions of "User:LuthfiShafwan"
(→INTERPRETASI GRAFIK) |
(→Tugas 2) |
||
| Line 152: | Line 152: | ||
=Tugas 2= | =Tugas 2= | ||
Tugas 2 ini menggunakan metode elemen hingga (1D Finite Element Method) dalam analisis perpindahan panas. Tujuannya adalah membuat aplikasi Python untuk menentukan distribusi suhu pada pipa dengan pemanasan seragam, di mana pipa memiliki suhu 0°C di kedua ujungnya kemudian interpretasikan hasil simulasinya dan kaitkan dengan DAI5 Framework | Tugas 2 ini menggunakan metode elemen hingga (1D Finite Element Method) dalam analisis perpindahan panas. Tujuannya adalah membuat aplikasi Python untuk menentukan distribusi suhu pada pipa dengan pemanasan seragam, di mana pipa memiliki suhu 0°C di kedua ujungnya kemudian interpretasikan hasil simulasinya dan kaitkan dengan DAI5 Framework | ||
| + | <body> | ||
| + | <h2>1. Persamaan Konduksi Panas (Hukum Fourier)</h2> | ||
| + | <p>Persamaan konduksi panas satu dimensi dalam kondisi steady-state tanpa adanya sumber panas internal (untuk aliran panas konduktif) adalah:</p> | ||
| + | <div class="equation"> | ||
| + | <p>d/dx (k * dT/dx) = 0</p> | ||
| + | </div> | ||
| + | <p>di mana:</p> | ||
| + | <ul> | ||
| + | <li><em>k</em> adalah konduktivitas termal SS 304 (W/m·K).</li> | ||
| + | <li><em>T</em> adalah suhu (°C atau K).</li> | ||
| + | <li><em>x</em> adalah posisi sepanjang pipa (m).</li> | ||
| + | </ul> | ||
| + | |||
| + | <h2>2. Persamaan Konduksi Panas dengan Sumber Panas</h2> | ||
| + | <p>Jika terdapat sumber panas seragam <em>Q</em> dalam pipa, persamaan konduksi panas menjadi:</p> | ||
| + | <div class="equation"> | ||
| + | <p>d/dx (k * dT/dx) + Q = 0</p> | ||
| + | </div> | ||
| + | <p>di mana <em>Q</em> adalah sumber panas per satuan volume (W/m<sup>3</sup>).</p> | ||
| + | |||
| + | <h2>3. Diskritisasi dengan Metode Elemen Hingga (FEM)</h2> | ||
| + | <p>Metode elemen hingga digunakan untuk mendiskritisasi persamaan diferensial parsial ini menjadi sistem persamaan linear. Matriks kekakuan lokal untuk elemen 1D diberikan oleh:</p> | ||
| + | <div class="equation"> | ||
| + | <p>K<sub>local</sub> = (k/Δx) [1 -1; -1 1]</p> | ||
| + | </div> | ||
| + | <p>di mana Δx adalah panjang elemen.</p> | ||
| + | |||
| + | <h2>4. Penyusunan Vektor Gaya</h2> | ||
| + | <p>Vektor gaya <em>F</em> diisi dengan kontribusi dari sumber panas seragam:</p> | ||
| + | <div class="equation"> | ||
| + | <p>F[i] = Q * Δx</p> | ||
| + | </div> | ||
| + | |||
| + | <h2>5. Sistem Persamaan Linear</h2> | ||
| + | <p>Setelah menyusun matriks kekakuan global <em>K</em> dan vektor gaya <em>F</em>, sistem persamaan linear yang perlu diselesaikan adalah:</p> | ||
| + | <div class="equation"> | ||
| + | <p>K * T = F</p> | ||
| + | </div> | ||
| + | <p>di mana:</p> | ||
| + | <ul> | ||
| + | <li><em>K</em> adalah matriks kekakuan global.</li> | ||
| + | <li><em>T</em> adalah vektor suhu pada simpul-simpul.</li> | ||
| + | <li><em>F</em> adalah vektor gaya total.</li> | ||
| + | </ul> | ||
| + | |||
| + | <h2>6. Kondisi Batas</h2> | ||
| + | <p>Kondisi batas (Dirichlet boundary conditions) diterapkan dengan menetapkan suhu tertentu di simpul-simpul yang terkait, seperti suhu 0°C di kedua ujung pipa.</p> | ||
| + | </body> | ||
[[File:CamScanner 11-11-2024 14.38-1--1.png|500px|center]] | [[File:CamScanner 11-11-2024 14.38-1--1.png|500px|center]] | ||
[[File:Carbon(5).png|500px|center]] | [[File:Carbon(5).png|500px|center]] | ||
Revision as of 19:05, 11 November 2024
Contents
Introduction
Nama saya muhammad luthfi shafwan, mahasiswa S2 Teknik Mesin peminatan Teknologi dan Sumber Daya Maritim angkatan 2024
Komputasi Teknik Pertemuan 1 (Pasca UTS) 29/10/2024
Pada pertemuan pertama ini, mahasiswa diperkenalkan dengan sebuah framework bernama DAI-5, yang dikembangkan oleh Dr. Ir. Ahmad Indra Siswantara. Framework ini didasari oleh konsep conscious thinking atau berpikir secara sadar. Landasan dari framework ini adalah falsafah yang beliau utarakan, yaitu "I'm my consciousness," yang menegaskan pentingnya kesadaran dalam setiap tindakan. Sebagai inisiator, beliau merumuskan framework ini menjadi empat tahapan penting:
(1) Intention, Menentukan niat/ide awal
(2) Initial Thinking, Mengeksplorasi dari ide yang kita inisiasikan sebelumnya
(3) Idealization, Penarikan solusi Dari ide tersebut kemudian mensimplifikasi sesuatu agar lebih ideal
(4) Instruction Set, Solusi ideal yang menjadi output pada tahapan sebelumnya, dikonversi menjadi sebuah tahapan sistematis Tahapan-tahapan ini merepresentasikan pentingnya pendekatan sistematis dalam berbagai aspek kehidupan.
Tugas 1
kasus distribusi tekanan pada geometri Oscillating Water Coloumn untuk 2 konfigurasi, 1 chamber 2 turbine dan 2 chamber 1 turbine
Pada pertemuan kali ini, Pak Dai memberikan arahan kepada mahasiswa untuk melakukan diskusi mengenai FEM (Finite Element Method) melalui platform ChatGPT. Diskusi ini akan mencakup beberapa pertanyaan yang sesuai dengan arahan beliau, dengan output yang diharapkan dapat menghubungkan konsep FEM dengan langkah-langkah yang terdapat dalam kerangka DAI-5. Kasus yang menjadi subjek diskusi melalui platform chatGPT kali ini adalah Finite Element Method (FEM) untuk Oscillating Water Column (OWC) dengan 2 konfigurasi (1 turbin 2 chamber dan 2 turbin 1 chamber)
hasil diskusi dengan ChatGPT mengenai FEM pada OWC dengan 2 konfigurasi
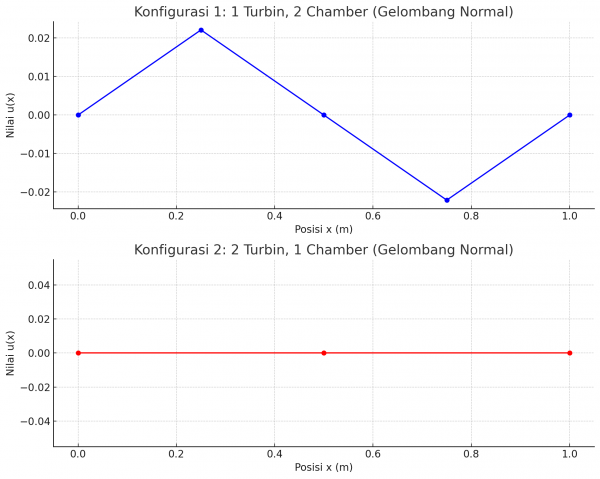
Grafik diatas merupakan output dari code yang di generate oleh chatGPT mengenai kasus ini dengan anggapan gelombang normal, dapat dilihat bahwa pada grafik pertama yaitu konfigurasi 1 (1 Turbin, 2 Chamber): Grafik menunjukkan variasi nilai u(x) di sepanjang posisi x dalam domain. Distribusi ini mengikuti pola sinusoidal yang diberikan oleh sumber gaya gelombang. Sementara pada konfigurasi 2 (2 Turbin, 1 Chamber): Grafik menunjukkan bahwa nilai u(x) tetap konstan di sepanjang domain, mencerminkan perbedaan dalam konfigurasi elemen dan pengaruhnya terhadap solusi.
Penerapan Framework DAI5 pada Algoritma FEM untuk OWC
Mengaitkan algoritma kasus Finite Element Method (FEM) untuk Oscillating Water Column (OWC) ini dengan framework DAI5 akan membantu memberikan struktur berpikir yang lebih sistematis dan terarah. Berikut adalah bagaimana algoritma ini dapat diterjemahkan ke dalam langkah-langkah DAI5:
1. Intention (Tujuan)
-
Tujuan:
Menyimulasikan dan memahami pengaruh konfigurasi yang berbeda pada geometri OWC terhadap distribusi tekanan atau kecepatan air di dalam chamber menggunakan metode FEM.
-
Pertanyaan yang ingin dijawab:
Bagaimana dua konfigurasi turbin dan chamber pada OWC memengaruhi hasil distribusi nilai 𝑢(𝑥) di sepanjang domain? Hasil ini penting untuk mengevaluasi efisiensi dan optimalitas setiap konfigurasi dalam menangkap energi gelombang.
-
Spesifikasi Output:
Grafik distribusi nilai 𝑢(𝑥) untuk dua konfigurasi (1 turbin 2 chamber dan 2 turbin 1 chamber), yang menunjukkan perbedaan pola hasil simulasi FEM.
2. Initial Thinking (Pemikiran Awal)
-
Pemahaman Sistem:
Sistem OWC ini dapat dimodelkan sebagai sistem gelombang yang mengalami difusi di dalam chamber, dengan konfigurasi turbin dan chamber yang berbeda untuk setiap simulasi.
-
Persamaan yang Digunakan:
Dalam konteks FEM, kita akan menggunakan persamaan diferensial linier sederhana yang menunjukkan hubungan antara koefisien difusi, gaya eksternal (gelombang sinusoidal), dan nilai solusi 𝑢(𝑥) pada setiap node.
-
Diskritisasi Domain:
Bagi domain menjadi elemen-elemen kecil, di mana setiap elemen memiliki dua node. Pilihan jumlah elemen ditentukan oleh konfigurasi yang ingin diuji:
- Konfigurasi 1: 4 elemen untuk 1 turbin dan 2 chamber.
- Konfigurasi 2: 2 elemen untuk 2 turbin dan 1 chamber.
-
Kondisi Batas:
Terapkan kondisi batas Dirichlet di kedua ujung domain untuk menetapkan nilai 𝑢(𝑥) = 0 pada titik awal dan akhir.
3. Idealization (Idealasi)
-
Ideal Model:
Untuk mencapai simulasi yang efisien dan akurat, kita perlu membuat asumsi tertentu:
- Sederhanakan domain menjadi panjang 1 meter untuk memudahkan perhitungan dan menjaga konsistensi antar-konfigurasi.
- Model Persamaan Linier untuk difusi, dengan anggapan bahwa interaksi antara chamber dan turbin dapat direpresentasikan oleh koefisien difusi 𝑘.
- Pembentukan Matriks Kekakuan dan Vektor Beban: Matriks kekakuan lokal disederhanakan menggunakan matriks elemen standar untuk metode elemen hingga satu dimensi, dan gaya eksternal dihitung sebagai sinyal sinusoidal.
-
Strategi Solusi:
- Perakitan Matriks Kekakuan dan Vektor Beban Global: Setiap elemen memiliki kontribusi kekakuan dan beban yang diakumulasi dalam matriks kekakuan dan vektor beban global.
- Pemecahan Sistem Persamaan Linier: Setelah perakitan matriks dan penerapan kondisi batas, selesaikan sistem persamaan 𝐾 ⋅ 𝑈 = 𝐹 untuk mendapatkan distribusi nilai 𝑢(𝑥).
-
Hasil Ideal yang Diinginkan:
Distribusi nilai 𝑢(𝑥) yang berbeda untuk setiap konfigurasi, menunjukkan variasi tekanan atau kecepatan partikel air di sepanjang domain, sesuai dengan interaksi antara turbin dan chamber dalam setiap konfigurasi.
4. Instruction Set (Set Instruksi)
Algoritma berikut menjabarkan setiap langkah yang perlu diambil untuk mengimplementasikan simulasi FEM untuk dua konfigurasi pada sistem OWC:
-
Definisikan Parameter Sistem:
Tetapkan panjang domain 𝐿, koefisien difusi 𝑘, amplitudo gelombang 𝐴, frekuensi sudut 𝜔, dan kondisi batas.
-
Diskritisasi Domain:
- Bagi domain menjadi elemen-elemen kecil.
- Hitung panjang setiap elemen ℎ = 𝐿/𝑛elements.
- Tentukan jumlah node berdasarkan jumlah elemen (node = elemen + 1).
-
Bentuk Matriks Kekakuan Lokal dan Vektor Beban:
- Hitung matriks kekakuan lokal 𝐾e untuk setiap elemen.
- Hitung gaya sinusoidal pada posisi tengah elemen untuk membentuk vektor beban lokal 𝐹e.
-
Perakitan Matriks Kekakuan Global dan Vektor Beban Global:
Gabungkan kontribusi dari setiap elemen ke dalam matriks kekakuan global 𝐾 dan vektor beban global 𝐹.
-
Terapkan Kondisi Batas:
Modifikasi matriks kekakuan 𝐾 dan vektor beban 𝐹 sesuai dengan kondisi batas Dirichlet di ujung domain.
-
Penyelesaian Sistem Persamaan Linier:
Gunakan solusi numerik untuk menyelesaikan 𝐾 ⋅ 𝑈 = 𝐹 sehingga mendapatkan nilai 𝑢(𝑥) di setiap node.
-
Visualisasi Hasil:
- Buat grafik yang menunjukkan distribusi nilai 𝑢(𝑥) di sepanjang domain untuk setiap konfigurasi.
- Bandingkan grafik hasil dari konfigurasi 1 (1 Turbin, 2 Chamber) dan konfigurasi 2 (2 Turbin, 1 Chamber).
Dengan mengikuti framework DAI5, kita dapat memahami bagaimana setiap tahap berpikir dalam mengembangkan algoritma simulasi ini berjalan dari pemahaman tujuan, pemikiran awal, idealisasi sistem, hingga langkah-langkah instruksi yang jelas untuk mencapai hasil akhir.
Tugas 2
Tugas 2 ini menggunakan metode elemen hingga (1D Finite Element Method) dalam analisis perpindahan panas. Tujuannya adalah membuat aplikasi Python untuk menentukan distribusi suhu pada pipa dengan pemanasan seragam, di mana pipa memiliki suhu 0°C di kedua ujungnya kemudian interpretasikan hasil simulasinya dan kaitkan dengan DAI5 Framework <body>
1. Persamaan Konduksi Panas (Hukum Fourier)
Persamaan konduksi panas satu dimensi dalam kondisi steady-state tanpa adanya sumber panas internal (untuk aliran panas konduktif) adalah:
d/dx (k * dT/dx) = 0
di mana:
- k adalah konduktivitas termal SS 304 (W/m·K).
- T adalah suhu (°C atau K).
- x adalah posisi sepanjang pipa (m).
2. Persamaan Konduksi Panas dengan Sumber Panas
Jika terdapat sumber panas seragam Q dalam pipa, persamaan konduksi panas menjadi:
d/dx (k * dT/dx) + Q = 0
di mana Q adalah sumber panas per satuan volume (W/m3).
3. Diskritisasi dengan Metode Elemen Hingga (FEM)
Metode elemen hingga digunakan untuk mendiskritisasi persamaan diferensial parsial ini menjadi sistem persamaan linear. Matriks kekakuan lokal untuk elemen 1D diberikan oleh:
Klocal = (k/Δx) [1 -1; -1 1]
di mana Δx adalah panjang elemen.
4. Penyusunan Vektor Gaya
Vektor gaya F diisi dengan kontribusi dari sumber panas seragam:
F[i] = Q * Δx
5. Sistem Persamaan Linear
Setelah menyusun matriks kekakuan global K dan vektor gaya F, sistem persamaan linear yang perlu diselesaikan adalah:
K * T = F
di mana:
- K adalah matriks kekakuan global.
- T adalah vektor suhu pada simpul-simpul.
- F adalah vektor gaya total.
6. Kondisi Batas
Kondisi batas (Dirichlet boundary conditions) diterapkan dengan menetapkan suhu tertentu di simpul-simpul yang terkait, seperti suhu 0°C di kedua ujung pipa.
</body>
Interpretasi Grafik
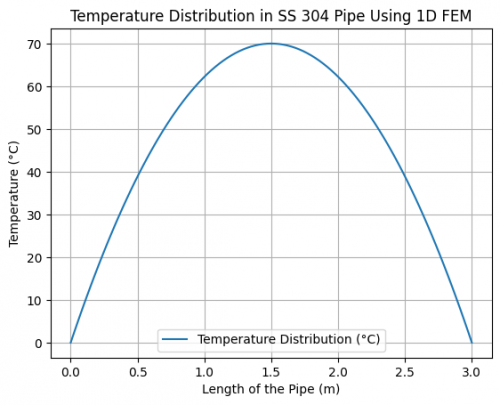
Grafik menunjukkan distribusi temperatur pada pipa SS 304 sepanjang 3 meter, di mana suhu pada kedua ujung pipa dijaga pada 0°C, menyebabkan suhu meningkat secara bertahap ke titik maksimum sekitar 70°C di tengah pipa sebelum menurun kembali. Hal ini mengindikasikan pemanasan seragam sepanjang pipa dan penyelesaian distribusi suhu dilakukan menggunakan metode elemen hingga (1D FEM).
Hubungan dengan Framework DAI5
Framework DAI5 terdiri dari lima tahap: Intention, Initial Thinking, Idealization, Instruction Set. Berikut cara algoritma FEM ini dihubungkan dengan DAI5: Framework DAI5 terdiri dari lima tahap: Intention (Tujuan), Initial Thinking (Pemikiran Awal), Idealization (Idealasi), Instruction Set (Set Instruksi), Implementation (Implementasi). Berikut cara algoritma FEM ini dihubungkan dengan DAI5:
- Intention (Tujuan):
- Tujuan utama adalah membuat aplikasi Python untuk menganalisis distribusi suhu di sepanjang pipa menggunakan metode FEM 1D dengan pemanasan seragam dan kondisi batas tertentu (0°C di kedua ujung).
- Initial Thinking (Pemikiran Awal):
- Pikirkan bagaimana masalah ini dapat diselesaikan menggunakan pendekatan numerik, seperti metode elemen hingga. Identifikasi parameter utama, seperti properti material (SS 304), panjang pipa, dan distribusi suhu.
- Idealization (Idealasi):
- Buat model matematika dari sistem fisik dengan menyederhanakannya menjadi model 1D yang dapat didiskritisasi. Asumsikan distribusi pemanasan seragam dan kondisi steady-state untuk mempermudah simulasi.
- Idealasi ini mencakup pemilihan model elemen hingga 1D dengan matriks kekakuan lokal dan global.
- Instruction Set (Set Instruksi):
- Susun langkah-langkah instruksi yang mencakup pengisian matriks kekakuan global, vektor gaya, penerapan kondisi batas, dan penyelesaian sistem persamaan. Rancang algoritma dalam bentuk kode Python yang jelas dan terstruktur.
- Implementation (Implementasi):
- Jalankan kode Python yang telah dibuat untuk mengimplementasikan solusi. Visualisasikan hasil distribusi suhu dan interpretasikan untuk memahami bagaimana suhu menyebar di sepanjang pipa berdasarkan parameter yang diberikan.