Difference between revisions of "Tarrant Anargiya Ziva"
| Line 77: | Line 77: | ||
[[Tank Design:]] | [[Tank Design:]] | ||
| − | '''To optimize a tube with a volume of | + | '''To optimize a tube with a fixed radius of 5 cm and a volume of 1000 cm³, we can find the height that minimizes the surface area of the tube. Here's the Python code to calculate the optimized height:''' |
| − | |||
import math | import math | ||
from scipy.optimize import minimize | from scipy.optimize import minimize | ||
| Line 108: | Line 107: | ||
| − | + | ||
'''Jari-jari teroptimasi: 5.41926305506462''' | '''Jari-jari teroptimasi: 5.41926305506462''' | ||
Revision as of 16:59, 11 June 2023
Introduction
Halo semua, perkenalkan nama saya Tarrant Anargiya Ziva, biasa dipanggil Tarrant
NPM : 2106652146
Kelas : Metode Numerik-03
"فَبِأَيِّ آلَاءِ رَبِّكُمَا تُكَذِّبَانِ"
[I] Consciousness
Consciousness refers to the state of being aware of and able to perceive both the external world and one's internal mental experiences. It is often described as the subjective experience of thoughts, sensations, emotions, and perceptions. While consciousness is a deeply complex and multifaceted phenomenon, it is generally characterized by qualities such as self-awareness, subjective experience, and the ability to process and integrate information.
[II] Hydrogen Storage
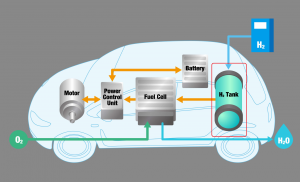
Bahan bakar hidrogen merupakan energi terbarukan yang dapat dikatakan bahan bakar alternatif ramah lingkungan dan berpotensi menggantikan bahan bakar bensin di masa yang akan datang. Bahan bakar hidrogen dapat dikonversi menjadi energi listrik menggunakan suatu unit yang dinamakan dengan hydrogen fuel cell.
Salah satu permasalahannya adalah cara penyimpanannya, karena volumetric energy density-nya yang rendah dan merupakan yang paling ringan serta paling sederhana dari semua elemen, lebih ringan dari helium, sehingga mudah hilang ke atmosfer.
Tantangan lainnya adalah titik didih hidrogen cair yang sangat rendah (−252,8°C), yang berarti hidrogen cair perlu disimpan secara cryogenic pada suhu rendah. Menyimpan hidrogen sebagai gas juga memiliki tantangan tersendiri karena biasanya memerlukan penggunaan tangki bertekanan tinggi (350-700 bar atau 5.000-10.000 psi).
Optimization
Spesifikasi : A) Kapasitas : 1 Liter B) Tekanan : 8 Bar
Material: Tangki harus dirancang untuk menahan persyaratan tekanan dan volume yang diinginkan. Faktor-faktor yang perlu dipertimbangkan meliputi ketebalan dinding, bentuk, dan metode perkuatan. Biasanya dapat komposit seperti karbon dan serat kaca, atau baja paduan tinggi seperti AISI 316L untuk tangki bertekanan tinggi.
Desain: Kita dapat mengambil bentuk silinder untuk meminimalisir tekanan yang terpusat pada sudut-sudut, jika mengambil bentuk yang memiliki sudut. Kita juga perlu memastikan desain tangki mematuhi standar-standar yang menentukan prinsip-prinsip desain tangki bertekanan. Selin itu, kita hrus mempertimbangkan faktor keamanan terhadap kegagalan, minimal 2.0 untuk tangki bertekanan. Dengan tangki silinder, tebal dinding (t) dapat dihitung menggunakan rumus berikut:
t = P x r / (σ - P)
P = tekanan dalam tangki (8 bar = 800.000 Pascal) r = Jari-Jari Tangki σ = Tegangan izin material tangki
Safety Measure: Hidrogen sangat mudah terbakar dan membutuhkan perlakuan khusus. Kita dapat menambahkan fitur keselamatan seperti perangkat pelepas tekanan, burst disc, dan sensor suhu untuk mengurangi potensi risiko.Tangki juga harus dilengkapi dengan katup pengaman tekanan atau safety valve untuk melindungi terhadap kondisi overpressure. -
Untuk tangki hidrogen 1 Liter, kita gunakan diameter 10 cm, maka kita cari tingginya dengan rumus volume :
1 Liter = 1000 cm^3
v = π x r x r x h
1000 = 3.14 x 5 x 5 x h
h= 12,738 cm^3
Pemilihan Material Material yang digunakan adalah sheet metal ASTM A36 dengan yield strength 36.000 Psi
Allowable Stress = 2/3 x sy = 24.000 Psi
Rumus ketebalan untuk arah tegangan longitudinal :
t = PR/(2SE + 0.4P)
E = 0,60 (Single-welded butt joint)
P = 8 bar = 116 Psi
R = 30 mm = 1,18 inch
S = 24.000 Psi
Corrosion allowance = 1 mm = 0,039 inch
t = 116 x (1,18+0,039)/ (2 x 24.000 x 0,60) + (0,4 x 116) t = 0,049 inch atau 1,24 mm
To optimize a tube with a fixed radius of 5 cm and a volume of 1000 cm³, we can find the height that minimizes the surface area of the tube. Here's the Python code to calculate the optimized height:
import math from scipy.optimize import minimize
def calculate_surface_area(radius, height):
base_area = math.pi * radius**2 lateral_area = 2 * math.pi * radius * height return base_area + lateral_area
def calculate_volume(radius, height):
return math.pi * radius**2 * height
def objective_function(height):
return calculate_surface_area(5, height)
def volume_constraint(height):
return calculate_volume(5, height) - 1000 # Constraint: volume - 1000 = 0
- Optimization
result = minimize(objective_function, x0=500, constraints={'type': 'eq', 'fun': volume_constraint}) optimized_height = result.x[0] optimized_surface_area = result.fun
- Print the optimized height and surface area
print(f"The optimized height for a tube with radius 5 cm is {optimized_height:.2f} cm.") print(f"The corresponding minimum surface area is {optimized_surface_area:.2f} cm².")
Jari-jari teroptimasi: 5.41926305506462
Tinggi teroptimasi: 10.838511985088449
Luas permukaan teroptimasi: 553.5810444905989
In the example above, we use the minimize function of the scipy module to solve optimization problems with limitations. The objective function is the object function that seeks the area of the surface, while the constraint function is a volume limit. We give the initial value x0 for fingers and heights, and the optimization results are stored in the result variable. As a result, we can obtain optimized radius, optimized heights, and optimized surface areas that are then displayed.
Reference
Office of Energy Efficiency & Renewable Energy. (2010). Hydrogen Storage. Energy.gov. https://www.energy.gov/eere/fuelcells/hydrogen-storage
What is Hydrogen Storage and How Does it Work? (n.d.). Www.twi-Global.com. https://www.twi-global.com/technical-knowledge/faqs/what-is-hydrogen-storage#WhyisitDifficulttoStoreHydrogen