Difference between revisions of "Shaquille Syahkhayru Hadis"
(→Final Report of Design & Optimization of Pressurized Hydrogen Storage) |
(→Final Report of Design & Optimization of Pressurized Hydrogen Storage) |
||
| Line 88: | Line 88: | ||
| − | Status: Optimal | + | '''Status: Optimal''' |
| − | Jumlah unit penyimpanan hidrogen yang akan dibeli: 5.0 | + | '''Jumlah unit penyimpanan hidrogen yang akan dibeli: 5.0''' |
| − | Total kapasitas penyimpanan: 5 liter | + | '''Total kapasitas penyimpanan: 5 liter''' |
| − | Total biaya: 500000 Rupiah | + | '''Total biaya: 500000 Rupiah''' |
| Line 126: | Line 126: | ||
[[File:grafik hidrogen.png|300px]] | [[File:grafik hidrogen.png|300px]] | ||
| + | |||
Kode tersebut difokuskan untuk mengoptimalkan penyimpanan hidrogen dengan mempertimbangkan keterbatasan kapasitas dan anggaran yang diberikan. Tujuan utamanya adalah untuk mengetahui jumlah unit penyimpanan hidrogen yang akan dibeli untuk mencapai total kapasitas penyimpanan maksimum, dengan tetap memenuhi batasan anggaran maksimum yang ditentukan. | Kode tersebut difokuskan untuk mengoptimalkan penyimpanan hidrogen dengan mempertimbangkan keterbatasan kapasitas dan anggaran yang diberikan. Tujuan utamanya adalah untuk mengetahui jumlah unit penyimpanan hidrogen yang akan dibeli untuk mencapai total kapasitas penyimpanan maksimum, dengan tetap memenuhi batasan anggaran maksimum yang ditentukan. | ||
Revision as of 13:02, 9 June 2023
RESUME PERTEMUAN 1 (26/05/2023)
Pada pertemuan pertama metode numerik bersama Bapak Dr. Ir. Ahmad Indra Siswantara atau yang biasa dipanggil Pak Dai, menjelaskan bahwa sebelum kita menyelesaikan suatu masalah kita terlebih dahulu harus memiliki consciousness atau kesadaran untuk berfikir dengan jernih agar dapat mendapatkan hasil yang terbaik. Bandura (1986) secara garis besar menyatakan kesadaran (consciousness) adalah menjadi sadar(being aware) atas kejadian kejadian eksternal yang terjadi di sekitar individu, apa yang dipikirkan, dirasakan, dan dilakukan. Jadi menurut saya, untuk kasus tersebut kita harus melakukan suatu pendekatan numerik karena kita harus sadar bahwa kita tidak dapat menemukan hasil yang eksak.
Saat perkuliahan Pak Dai melemparkan suatu kasus kepada kita untuk mencari penyelesai dari (x^2 - 1)/(x - 1). Menurut saya cara yang paling tepat untuk menyelesaikannya adalah dengan cara menjabarkan persamaan tersebut menjadi (x+1)(x-1)/(x-1) sehingga nilai x adalah 2, sedangkan jika kita langsung mensubstitusikan nilai 1 ke persamaan awal maka didapatkan hasil 0/0 dimana nilai tersebut tidak terdefinisi. Maka dari itu kita menggunakan penjabaran agar mendapatkan hasil yang mutlak yaitu 2. Pak Dai juga memberika kita sebuah tugas yaitu merancang tabung hidrogen yang berisi 1 liter dengan tekanan 8 bar dan budget untuk pembuatannya dibawah Rp500.000,00. Pada akhir sesi perkuliahan beliau juga menyampaikan agar kita sebagai mahasiswa datang kelas tidak hanya untuk absen saja tapi untuk mendapatkan pelajaran yang bisa merubah kita kedepannya.
Design & Optimization of Pressurized Hydrogen Storage
Case Study: Desain dan Mengoptimalkan Tekanan dari Penyimpanan Hidrogen
Spesifikasi
Kapasitas: 1 L
Tingkat Tekanan: 8 bar
Biaya Maksimum: Rp500.000,00
A pressurized hydrogen storage system's design and optimization must take specific needs, a budget of Rp 500.000,-, into account, as well as material choices, design parameters, and cost-cutting techniques. The following is a step-by-step method to assist you with the design:
ChatGPT
Certainly! Here's a step-by-step method for designing and optimizing a pressurized hydrogen storage system within a budget of Rp 500.000,- while considering specific needs, material choices, design parameters, and cost-cutting techniques:
Determine Requirements: Identify the specific needs and requirements of the hydrogen storage system, such as the desired capacity, pressure rating, and any specific operational conditions.
Material Selection: Research and compare different materials suitable for hydrogen storage, considering factors such as weight, strength, corrosion resistance, and cost. Materials like carbon fiber reinforced polymer (CFRP), high-strength stainless steel, or aluminum alloys may be considered, depending on availability and cost.
Tank Dimensions: Calculate the required dimensions of the storage tank based on the desired capacity and pressure rating, while considering safety factors. Optimize the dimensions to minimize material usage and cost. Consider a cylindrical shape for an efficient volume-to-surface ratio.
Tank Design: Design the tank structure based on the chosen material, dimensions, and pressure requirements. Ensure that the tank design can withstand the desired pressure by analyzing stress and strain distribution. Consider safety features such as pressure relief valves and burst disks to prevent over-pressurization.
Cost Optimization: To optimize costs, consider the following strategies: Minimize material usage by optimizing the tank dimensions and design. Explore cost-effective manufacturing techniques such as filament winding, bladder molding, or sheet metal fabrication. Simplify the design and reduce the number of additional components to minimize costs. Consider purchasing materials in bulk or sourcing cost-effective alternatives without compromising safety.
Safety Considerations: Ensure compliance with safety standards and regulations for pressurized hydrogen storage systems. Conduct thorough testing and quality control measures to ensure the safety and reliability of the storage system. Allocate a portion of the budget for safety features, inspections, and testing procedures.
Iterate the design process, considering the cost analysis results and identifying areas where further cost optimization can be achieved.
Make adjustments to the design, materials, or manufacturing processes to align with the budget constraints.
Remember that designing a pressurized hydrogen storage system within a limited budget can be challenging. It may require compromises in terms of material selection, capacity, or pressure rating. Balancing safety, performance, and cost is crucial throughout the design and optimization process.
Final Report of Design & Optimization of Pressurized Hydrogen Storage
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen = 1
# Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x
# Kendala
def kendala(anggaran):
return budget_maksimal - (harga_per_unit * anggaran)
kendala_anggaran = {'type': 'ineq', 'fun': kendala}
# Nilai awal
x0 = 0
# Batasan
batas = [(0, None)]
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran])
# Menampilkan hasil
print("Status:", solusi.success and "Optimal" or "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
Kode di atas menggunakan fungsi objektif untuk memaksimalkan jumlah unit penyimpanan hidrogen yang akan dibeli. Kendala anggaran ditetapkan menggunakan constraint function, yang memastikan bahwa total biaya tidak melebihi anggaran maksimum yang diberikan. Hasilnya akan menampilkan jumlah unit yang harus dibeli, total kapasitas penyimpanan, dan total biaya yang dibutuhkan.
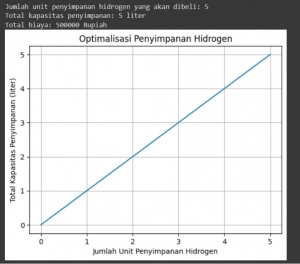
Status: Optimal
Jumlah unit penyimpanan hidrogen yang akan dibeli: 5.0
Total kapasitas penyimpanan: 5 liter
Total biaya: 500000 Rupiah
Kode yang menunjukkan kepada kita grafik optimalisasi penyimpanan hidrogen dengan mempertimbangkan kapasitas dan batasan anggaran yang diberikan.
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen
kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x * kapasitas_per_unit
# Kendala
def kendala(anggaran):
return budget_maksimal - (harga_per_unit * anggaran)
kendala_anggaran = {'type': 'ineq', 'fun': kendala}
# Nilai awal
x0 = 0
# Batasan
batas = [(0, None)]
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran])
# Menampilkan hasil
print("Status:", solusi.success and "Optimal" or "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
Kode tersebut difokuskan untuk mengoptimalkan penyimpanan hidrogen dengan mempertimbangkan keterbatasan kapasitas dan anggaran yang diberikan. Tujuan utamanya adalah untuk mengetahui jumlah unit penyimpanan hidrogen yang akan dibeli untuk mencapai total kapasitas penyimpanan maksimum, dengan tetap memenuhi batasan anggaran maksimum yang ditentukan.
Di dalam kode, diulangi untuk mencoba setiap kemungkinan jumlah unit yang dibeli dalam batasan anggaran. Setiap kuantitas unit diuji untuk menghitung total kapasitas penyimpanan dan total biaya terkait. Jika total kapasitas yang dihasilkan melebihi total kapasitas terbaik sebelumnya dan total biaya masih dalam batas anggaran, maka solusi optimal diperbarui.
Selain itu, kode membuat grafik yang menunjukkan hubungan antara jumlah unit penyimpanan hidrogen yang akan dibeli dan total kapasitas penyimpanan yang diperoleh. Grafik ini memberikan representasi visual tentang bagaimana kapasitas total berubah saat unit penyimpanan hidrogen tambahan ditambahkan.
Jadi fokus utama dari kode adalah menemukan solusi optimal untuk memaksimalkan kapasitas penyimpanan hidrogen dengan mempertimbangkan batasan anggaran maksimum, serta memberikan pemahaman visual melalui grafik.