Difference between revisions of "Rahmat Raviansyah"
(→Geometrical Constrain) |
(→Geometrical Constrain) |
||
| Line 101: | Line 101: | ||
| − | |||
| − | |||
| − | # Konstanta dan parameter | + | # Konstanta dan parameter |
| − | pressure = 8 # Bar | + | pressure = 8 # Bar |
| − | volume = 1 # Liter | + | volume = 1 # Liter |
| − | material_stress = 275 # MPa (Stainless Steel 316) | + | material_stress = 275 # MPa (Stainless Steel 316) |
| − | safety_factor = 2 # Faktor keamanan | + | safety_factor = 2 # Faktor keamanan |
| − | # Fungsi objektif untuk mencari luas permukaan minimum | + | # Fungsi objektif untuk mencari luas permukaan minimum |
| − | def objective_function(x): | + | def objective_function(x): |
r = x[0] | r = x[0] | ||
h = x[1] | h = x[1] | ||
| Line 117: | Line 115: | ||
return surface_area | return surface_area | ||
| − | # Fungsi constraint untuk mempertahankan volume 1 liter | + | # Fungsi constraint untuk mempertahankan volume 1 liter |
| − | def volume_constraint(x): | + | def volume_constraint(x): |
r = x[0] | r = x[0] | ||
h = x[1] | h = x[1] | ||
return volume - math.pi * r**2 * h | return volume - math.pi * r**2 * h | ||
| − | # Fungsi constraint untuk mempertahankan tekanan di bawah batas kekuatan material | + | # Fungsi constraint untuk mempertahankan tekanan di bawah batas kekuatan material |
| − | def pressure_constraint(x): | + | def pressure_constraint(x): |
r = x[0] | r = x[0] | ||
h = x[1] | h = x[1] | ||
| Line 131: | Line 129: | ||
return stress - (pressure * r) / (2 * material_stress) - (pressure * h) / (4 * material_stress) | return stress - (pressure * r) / (2 * material_stress) - (pressure * h) / (4 * material_stress) | ||
| − | # Menggunakan metode minimize dari library scipy untuk mencari solusi optimal | + | # Menggunakan metode minimize dari library scipy untuk mencari solusi optimal |
| − | x0 = [0.1, 0.1] # Tebakan awal untuk radius dan tinggi tabung | + | x0 = [0.1, 0.1] # Tebakan awal untuk radius dan tinggi tabung |
| − | bounds = ((0.01, None), (0.01, None)) # Batasan non-negatif untuk radius dan tinggi | + | bounds = ((0.01, None), (0.01, None)) # Batasan non-negatif untuk radius dan tinggi |
| − | constraints = ( | + | constraints = ( |
| − | + | {'type': 'eq', 'fun': volume_constraint}, # Constraint volume 1 liter | |
| − | + | {'type': 'ineq', 'fun': pressure_constraint} # Constraint tekanan di bawah batas kekuatan material | |
) | ) | ||
| − | solution = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=constraints) | + | solution = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=constraints) |
| − | # Menghitung dimensi optimal | + | # Menghitung dimensi optimal |
| − | radius_optimal = solution.x[0] | + | radius_optimal = solution.x[0] |
| − | height_optimal = solution.x[1] | + | height_optimal = solution.x[1] |
| − | surface_area_optimal = objective_function(solution.x) | + | surface_area_optimal = objective_function(solution.x) |
| − | # Menampilkan hasil | + | # Menampilkan hasil |
| − | print("Optimal Dimensions:") | + | print("Optimal Dimensions:") |
| − | print(f"Radius: {radius_optimal} m") | + | print(f"Radius: {radius_optimal} m") |
| − | print(f"Height: {height_optimal} m") | + | print(f"Height: {height_optimal} m") |
| − | print(f"Surface Area: {surface_area_optimal} m^2") | + | print(f"Surface Area: {surface_area_optimal} m^2") |
Revision as of 10:58, 9 June 2023
Contents
Resume Minggu Pertama
Metode numerik merupakan teknik penggunaan matematika dan algoritma komputasi untuk menyelesaikan masalah dalam bentuk perhitungan atau analisis yang melibatkan angka dan data numerik. Meskipun metode numerik sering dikaitkan dengan aplikasi dalam ilmu komputer, teknik ini juga memiliki manfaat yang relevan dalam kehidupan sehari-hari. Berikut adalah beberapa contoh manfaat metode numerik dalam kehidupan sehari-hari:
1.Pengelolaan keuangan: Metode numerik dapat digunakan dalam perencanaan keuangan pribadi, seperti perhitungan bunga, investasi, dan pinjaman. Dengan menggunakan metode numerik, seseorang dapat menghitung pembayaran bulanan hipotek atau pinjaman, menentukan waktu yang dibutuhkan untuk mencapai tujuan tabungan, atau mengoptimalkan investasi.
2.Pengolahan gambar dan video: Metode numerik digunakan dalam pengolahan gambar dan video, seperti kompresi data, restorasi gambar, dan analisis citra. Metode numerik memungkinkan pemrosesan gambar dan video yang lebih efisien dan akurat, termasuk perbaikan kualitas gambar, deteksi objek, dan analisis pola.
3.Prediksi cuaca: Meteorologi modern bergantung pada metode numerik untuk memprediksi cuaca. Model matematika kompleks digunakan untuk memproses data cuaca dari berbagai sumber, seperti satelit dan stasiun cuaca, dan menghasilkan prediksi cuaca jangka pendek maupun jangka panjang.
4.Desain produk: Metode numerik digunakan dalam desain produk untuk memprediksi dan mengoptimalkan kinerja suatu produk sebelum produksi fisik dilakukan. Simulasi numerik memungkinkan insinyur untuk menganalisis dan memprediksi perilaku produk dalam berbagai kondisi, seperti kekuatan struktural, aliran fluida, atau karakteristik termal.
5.Pengembangan obat: Dalam penelitian farmasi dan pengembangan obat, metode numerik digunakan untuk memodelkan interaksi molekuler dan meramalkan efek obat pada organisme. Metode ini mempercepat proses desain obat baru dan membantu mengidentifikasi kandidat yang paling potensial sebelum uji klinis dilakukan.
6.Optimisasi transportasi: Metode numerik digunakan dalam optimisasi rute transportasi, pengelolaan lalu lintas, dan perencanaan transportasi perkotaan. Algoritma yang berbasis metode numerik dapat membantu mengurangi kemacetan lalu lintas, meningkatkan efisiensi rute pengiriman, dan merencanakan pergerakan optimal dalam sistem transportasi yang kompleks.
7.Analisis data dan statistik: Metode numerik juga penting dalam analisis data dan statistik. Dalam kehidupan sehari-hari, kita sering menghadapi data yang kompleks dan besar, dan metode numerik dapat digunakan untuk menganalisis data ini, menemukan pola, membuat prediksi, atau mengidentifikasi tren.
Metode numerik memiliki peran penting dalam perhitungan dan analisis dalam industri perkapalan. Beberapa manfaat metode numerik dalam perhitungan dunia perkapalan meliputi:
1.Perhitungan kekuatan struktur: Metode numerik digunakan dalam perhitungan kekuatan struktur kapal. Dengan menggunakan model matematika dan simulasi numerik, insinyur dapat memprediksi bagaimana kapal akan merespons beban dan gaya eksternal, seperti gelombang laut atau beban angin. Hal ini memungkinkan mereka untuk mengoptimalkan desain struktur kapal, memastikan kekuatan dan keamanannya.
2.Analisis hidrodinamika: Metode numerik digunakan untuk menganalisis perilaku hidrodinamika kapal, termasuk hambatan gerak, performa propulsi, dan kestabilan kapal. Simulasi numerik memungkinkan insinyur untuk memprediksi gaya-gaya hidrodinamika yang bekerja pada kapal dalam berbagai kondisi, seperti pergerakan di air tenang atau di tengah gelombang besar. Informasi ini dapat digunakan untuk merancang kapal yang lebih efisien dan stabil.
3.Optimisasi desain kapal: Metode numerik juga digunakan dalam optimisasi desain kapal. Dengan memanfaatkan algoritma optimisasi dan simulasi numerik, insinyur dapat mencari kombinasi desain yang memberikan kinerja terbaik dalam hal kecepatan, efisiensi bahan bakar, atau stabilitas. Hal ini memungkinkan pengembangan kapal yang lebih efisien dan ramah lingkungan.
4.Simulasi manuver kapal: Metode numerik digunakan untuk melakukan simulasi manuver kapal, seperti berlabuh, berbelok, atau merapat ke dermaga. Dengan menggunakan model matematika yang tepat, simulasi numerik dapat membantu memprediksi perilaku kapal saat melakukan manuver dan memastikan keselamatan operasi.
5.Dinamika fluida komputasional (CFD): Metode numerik CFD digunakan dalam perhitungan aliran fluida sekitar kapal. Ini termasuk analisis aliran air di sekitar lambung kapal, pembangkitan gelombang, dan interaksi antara kapal dan air. Simulasi CFD memungkinkan insinyur untuk memperoleh pemahaman yang mendalam tentang kinerja hidrodinamika kapal, sehingga mempengaruhi perancangan dan efisiensi kapal.
6.Analisis kebisingan dan getaran: Metode numerik digunakan untuk menganalisis kebisingan dan getaran pada kapal. Simulasi numerik memungkinkan insinyur untuk memprediksi tingkat kebisingan dan getaran yang dihasilkan oleh mesin, sistem propulsi, atau interaksi struktur pada kapal. Hal ini membantu dalam merancang kapal yang lebih nyaman bagi awak dan penumpangnya.
Dalam industri perkapalan, metode numerik memainkan peran penting dalam perhitungan dan analisis yang berkaitan dengan kekuatan struktur, hidrodinamika, optimisasi desain, manuver, dinamika fluida
Design and optimization of pressurized hydrogen storage systems
Obj (Design and Optimization)
Spec ( Capacity 1L Pressure Level 8 bar )
Cost not to be exceeded 500K Rupiah
Design and optimization of pressurized hydrogen storage systems involve several key considerations to ensure safe and efficient operation. Here's a general framework for designing and optimizing such a system:
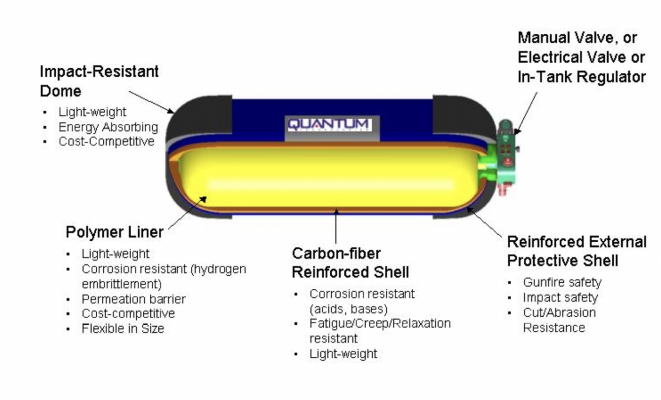
Storage Tank Selection: Choose a storage tank material that can withstand high-pressure hydrogen, such as carbon fiber reinforced polymer (CFRP) or metal alloys (e.g., aluminum or stainless steel). Consider factors like weight, cost, volumetric capacity, and safety when selecting the tank.
Tank Sizing: Determine the required storage capacity based on the system's hydrogen demand and desired operational autonomy. Consider factors like energy density, refueling frequency, and available space for installation.
Safety Measures: Incorporate safety features such as pressure relief devices, burst disks, and pressure sensors to prevent over-pressurization and ensure safe operation. Consider the design and location of the storage system to minimize potential risks and hazards.
Optimal Operating Pressure: Determine the optimal operating pressure range based on factors like hydrogen purity requirements, material limitations, and system efficiency. Balancing higher pressure for increased storage capacity with lower pressure for safety and cost considerations is crucial.
Thermal Management: Incorporate an efficient cooling system to manage heat generated during hydrogen compression and ensure the storage system operates within safe temperature limits. Consider options such as passive cooling through heat sinks or active cooling using fans, coolants, or heat exchangers.
Leak Detection and Mitigation: Implement leak detection systems to promptly identify and locate any hydrogen leaks. Use suitable materials, seals, and joint designs to minimize the risk of leaks. Consider incorporating automated shutdown mechanisms in case of a leak.
System Integration: Optimize the overall design by integrating the storage system with other components, such as a hydrogen generation system, fuel cell, or refueling infrastructure. Consider factors like system efficiency, compatibility, and ease of integration.
Performance Monitoring and Maintenance: Install sensors and monitoring systems to continuously track pressure, temperature, and other critical parameters. Establish a regular maintenance schedule to ensure the system remains in optimal condition and address any potential issues promptly.
Cost Analysis: Perform a cost analysis considering factors like tank material, manufacturing costs, safety measures, maintenance, and operational expenses. Optimize the design to achieve a balance between performance and cost efficiency. It is important to note that designing and optimizing a pressurized hydrogen storage system requires expertise in engineering, safety regulations, and material science. It's advisable to consult with experts in the field or specialized engineering firms for a comprehensive and accurate design suited to your specific requirements and local regulations.
Final Report of Design and Optimization of Pressurized Hydrogen Storage
Spec Hydrogen Tank
Capacity : 1 liter Pressure : 8 bar Cost : Rp500.000,00
Geometrical Constrain
Kode yang disediakan memanfaatkan algoritme pengoptimalan yang diimplementasikan dalam Python dan memanfaatkan fitur canggih dari pustaka NumPy dan SciPy. Tujuan dari seperangkat aturan ini adalah untuk menentukan radius dan tinggi tangki penyimpanan yang optimal dengan luas permukaan minimum dan jumlah hidrogen yang ditentukan. Integrasi NumPy memungkinkan operasi matematika yang efisien dan manipulasi array, SciPy menyediakan teknik dan algoritme pengoptimalan tingkat lanjut.
# Konstanta dan parameter pressure = 8 # Bar volume = 1 # Liter material_stress = 275 # MPa (Stainless Steel 316) safety_factor = 2 # Faktor keamanan
# Fungsi objektif untuk mencari luas permukaan minimum def objective_function(x): r = x[0] h = x[1] surface_area = math.pi * r * (r + math.sqrt(r**2 + h**2)) return surface_area
# Fungsi constraint untuk mempertahankan volume 1 liter def volume_constraint(x): r = x[0] h = x[1] return volume - math.pi * r**2 * h
# Fungsi constraint untuk mempertahankan tekanan di bawah batas kekuatan material def pressure_constraint(x): r = x[0] h = x[1] stress = pressure * 10 # Bar to MPa cross_sectional_area = math.pi * r**2 return stress - (pressure * r) / (2 * material_stress) - (pressure * h) / (4 * material_stress)
# Menggunakan metode minimize dari library scipy untuk mencari solusi optimal
x0 = [0.1, 0.1] # Tebakan awal untuk radius dan tinggi tabung
bounds = ((0.01, None), (0.01, None)) # Batasan non-negatif untuk radius dan tinggi
constraints = (
{'type': 'eq', 'fun': volume_constraint}, # Constraint volume 1 liter
{'type': 'ineq', 'fun': pressure_constraint} # Constraint tekanan di bawah batas kekuatan material
)
solution = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=constraints)
# Menghitung dimensi optimal radius_optimal = solution.x[0] height_optimal = solution.x[1] surface_area_optimal = objective_function(solution.x)
# Menampilkan hasil
print("Optimal Dimensions:")
print(f"Radius: {radius_optimal} m")
print(f"Height: {height_optimal} m")
print(f"Surface Area: {surface_area_optimal} m^2")
Dari hasil pengkodean, kita dapat menyimpulkan bahwa dimensi optimal untuk tangki silinder dengan rasio tinggi terhadap jari-jari 2 dicapai dengan meminimalkan luas permukaan.
Secara spesifik, tangki tersebut memiliki:
Radius: 0.4828024615119047 m
Height: 1.3655610390977921 m
Surface Area: 2.9291835114645908 m^2
Material Stainless Steel 316
End Cap Fillet
Penggunaan geometri silinder murni untuk tangki penyimpanan dapat menimbulkan bahaya karena konsentrasi tegangan di sudut. Untuk meminimalkan konsentrasi tegangan dan mengurangi luas permukaan sambil mempertahankan volume yang sama, akan lebih efisien jika menggunakan bentuk tutup ujung torik. Bentuk ini bisa dicapai dengan menambahkan tenggorokan dengan setengah jari-jari tangki. Pemrosesan fillet menarik kurva lembut untuk mengurangi konsentrasi stres. Penyesuaian parameter geometris diperlukan untuk mengkompensasi pengurangan volume akibat fillet. Dengan menghitung laju pengurangan luas penampang, kita dapat menerapkannya secara terbalik ke volume yang diinginkan untuk mendapatkan batasan baru untuk peningkatan volume.
Material Strength Constraints
# Fungsi untuk menghitung ketebalan minimal tabung gas hidrogen def calculate_thickness(radius, pressure, material_yield_strength): hoop_stress = pressure * radius / thickness safety_factor = 2 # Faktor keamanan (disesuaikan sesuai persyaratan desain) allowable_stress = material_yield_strength / safety_factor thickness_min = hoop_stress * radius / (2 * allowable_stress - hoop_stress) return thickness_min
# Input parameter radius = 10 # Radius tabung dalam cm pressure = 8 # Tekanan dalam bar material_yield_strength = 567 # Kuat luluh bahan dalam MPa (contoh: Stainless Steel 316)