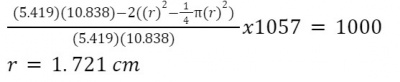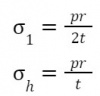Audry Jonathan P. T. Sitompul

Introduction

Pagi Mesin!

Assalamu'alaikum Wr. Wb.

Halo semua! Perkenalkan, saya Audry Jonathan P. T. Sitompul, akrab dipanggil Jo, dengan NPM 2106709283. Saya adalah mahasiswa Program Studi S1 Teknik Mesin angkatan 2021. Berikut adalah resume-resume saya selama pembelajaran di kelas Metode Numerik 01.

"Trust the process" Kalimat tersebut merupakan motto hidup saya agar selalu memaknai consciousness dalam setiap hal yang saya lakukan.

Tugas Hydrogen Storage Optimazition

Method To Optimaze Hydrogen Storage Design

In this study case i will use a commonly used numerical method called "particle swarm optimization" (PSO):

1. Define the Problem: Clearly state the objective function that represents the performance criteria of the hydrogen storage system. It could be maximizing the storage capacity, minimizing the weight or volume, or optimizing any other relevant parameter.

2. Define Variables and Constraints: Identify the variables that can be adjusted to optimize the system, such as tank dimensions, materials, operating conditions, etc. Also, define any constraints that need to be satisfied, such as pressure limits, safety requirements, or cost considerations.

3. Initialize the Swarm: Create a population of potential solutions (particles) that represent different configurations of the hydrogen storage system. Randomly initialize their positions and velocities within the search space.

4. Evaluate Fitness: Evaluate the fitness of each particle by applying the objective function to its corresponding configuration. This step involves performing calculations and simulations to determine the system's performance for each particle.

5. Update Particle's Best Position: For each particle, compare its fitness with the best fitness achieved by that particle so far. If the current fitness is better, update the particle's best position accordingly.

6. Update Global Best Position: Identify the particle with the best fitness among all the particles and record its position as the global best position found so far.

7. Update Velocities and Positions: Update the velocities and positions of each particle based on its own best position and the global best position. This step involves using mathematical equations that incorporate inertia, cognitive, and social parameters to guide the particles' movement.

8. Repeat: Repeat steps 4 to 7 until a termination criterion is met. This criterion could be a maximum number of iterations, reaching a desired fitness threshold, or other convergence criteria.

9. Extract Optimal Solution: Once the algorithm terminates, the particle with the best fitness (global best) represents the optimized design and configuration of the hydrogen storage system. Extract the corresponding parameters and evaluate their values.

10. Validate and Refine: Validate the optimal solution obtained by implementing it in practical applications or conducting further simulations. Refine the solution if necessary based on additional constraints or considerations.

Particle swarm optimization is just one of many numerical methods available for optimization problems. Depending on the specific characteristics of the hydrogen storage system and the optimization goals, other methods like genetic algorithms, simulated annealing, or gradient-based optimization techniques may also be applicable.

Final Project To Optimaze Hydrogen Storage Design

Design of Pressurized Hydrogen Storage

Pressurized hydrogen storage refers to the storage of hydrogen gas at high pressures in a container or vessel. Hydrogen gas, which is highly compressible, can be stored at pressures ranging from a few hundred to several thousand pounds per square inch (psi). By compressing hydrogen, it is possible to store larger quantities of the gas within a smaller volume, making it more practical for transportation and industrial applications.

Simple example design of a hydrogen tank (source: toyota)

Requirements Given

The specific requirements are 1 liter (1000 cm^3) of Hydrogen with 8 bar (800 kPa) Pressure with a maximum cost of Rp 500.000

Constraints Used

Geometrical Constraint : The geometrical constraint guarantees that the storage system design adheres to specific volume requirements. By imposing limitations on the volume or dimensions of the storage tank, one can optimize factors like radius and height to ensure that the tank can accommodate the desired 1-liter volume (equivalent to 1000 cm^3). This constraint ensures that the storage tank is appropriately sized and fits within the given space.

Material Strength Constraint : The material strength constraint focuses on selecting a material capable of withstanding the high-pressure conditions within the hydrogen storage system. Hydrogen is stored at elevated pressures (8 bar or 800 kPa), and choosing a material with suitable strength characteristics is crucial for ensuring safety and integrity. By applying this constraint, it ensures that the chosen material, such as AISI 316 austenitic stainless steel, possesses the necessary mechanical properties to withstand pressure and prevent any material failures or leaks.

Budget Constraint : The budget constraint sets a limit on the cost of the pressurized hydrogen storage system. By considering this constraint, it ensures that the optimization model takes into account the cost-effectiveness of the design. The budget constraint aids in selecting cost-efficient materials and optimizing geometrical parameters to meet the required specifications while remaining within the allocated budget of Rp 500,000. This constraint guarantees that the final design is financially feasible and aligns with the available resources.

Geometrical Constraint

In our scenario, the goal is to minimize the surface area while ensuring that the volume remains constant at 1 liter or 1000 cubic centimeters. By using an optimization function in Python, we can calculate the optimal values for the radius and height of a cylinder that satisfy both criteria.

import scipy.optimize as optimize
import math


# Constants
volume = 1000  # Desired volume in cubic centimeters


# Objective function
def objective(x):
    radius, height = x
    surface_area = 2 * np.pi * radius * (radius + height)
    return surface_area


# Constraint function
def constraint(x):
    radius, height = x
    volume = np.pi * radius**2 * height
    return volume - 1000


# Optimization
initial_guess = [1.0, 10]  # Initial guess for radius and height
bounds = [(0, None), (0, None)]  # Bounds for radius and height (non-negative values)
constraints = [{'type': 'ineq', 'fun': constraint}]  # Volume constraint
result = minimize(objective, initial_guess, bounds=bounds, constraints=constraints)


# Extract optimal radius and height
optimal_radius = result.x[0]
optimal_height = result.x[1]
minimum_surface_area = result.fun


# Display the computed optimal radius, height, and surface area
print("Optimal Radius:", optimal_radius)
print("Optimal Height:", optimal_height)
print("Minimum Surface Area:", minimum_surface_area)

In this code, we use the minimize_scalar function from the SciPy library to perform the optimization separately for the radius and height. The objective function calculates the surface area of the cylinder, while the constraint function enforces the desired volume of 1000 cubic centimeters. We define bounds to ensure non-negative values for radius and height.

First, we optimize for the minimum radius by keeping the height fixed at the initial guess value. Then, we optimize for the minimum height by keeping the radius fixed at the initial guess value. Finally, we compute the minimum surface area using the obtained optimal radius and height.

The results for the minimum radius, minimum height, and minimum surface area are 
Optimal Radius: 5.419259622871326
Optimal Height: 10.838525719677232
Minimum Surface Area: 553.5810446887042

End Cap Fillet

Using a cylindrical shape for the storage tank can pose a safety risk due to stress concentration areas or potential failure points at the corners of the ends. To mitigate this i will curved shapes at the ends to reduce stress concentration. Since our objective is to minimize surface area while maintaining the same volume, the most efficient choice would be a torispherical end cap shape. This shape can be viewed as a cylindrical shape with partial filleting. However, the addition of filleting reduces the overall volume of the structure. Therefore, we need to adjust the geometrical parameters to compensate for this reduction caused by the filleting and ensure the desired volume is maintained.

Fillet Tank(source: researchgate)

Material Strength Constraints

In our specific scenario, the hydrogen tank with a volume of 1 liter has a maximum pressure limit of 8 bar.

Within a cylindrical component with thin walls, there are two primary types of stress: circumferential (hoop) stress and longitudinal stress. To calculate the hoop stress and longitudinal stress, the following formulas can be used.

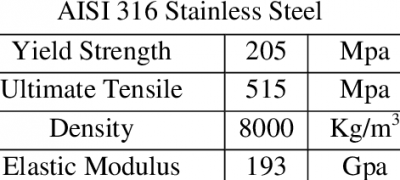
For this case we use High-Strength Steel: Steel alloys AISI 316 austenitic stainless steel because AISI 316 are commonly used due to their high strength, good ductility, and resistance to hydrogen embrittlement. Steel tanks can withstand high pressures and are relatively cost-effective.

AISI 316 Austenitic Stainless Steel Mechanical Properties, (source:researchgate)

Taking a conservative approach of setting the minimum thickness to be in between 1.59mm and 4mm, thereby 2.8mm, we will begin the iteration of the thickness from 2.80mm up to 11.04mm at increments of 0.01mm for precision.

r = 5.419e-2
p = 800000
t = 2.8e-3

while t < 11e-3:
  hoop = (r * p)/(t)
  print('for thickness', t, 'hoop stress =', hoop, "Pa")
  t += 0.1e-3
  if hoop > 205e9:
    break

for thickness 0.0028 hoop stress = 15482857.142857144 Pa
for thickness 0.0029 hoop stress = 14948965.517241381 Pa
for thickness 0.0029999999999999996 hoop stress = 14450666.666666668 Pa
for thickness 0.0030999999999999995 hoop stress = 13984516.12903226 Pa
for thickness 0.0031999999999999993 hoop stress = 13547500.000000004 Pa
for thickness 0.003299999999999999 hoop stress = 13136969.696969701 Pa
for thickness 0.003399999999999999 hoop stress = 12750588.235294122 Pa
for thickness 0.0034999999999999988 hoop stress = 12386285.714285718 Pa
for thickness 0.0035999999999999986 hoop stress = 12042222.222222228 Pa
for thickness 0.0036999999999999984 hoop stress = 11716756.756756762 Pa
for thickness 0.0037999999999999983 hoop stress = 11408421.052631585 Pa
for thickness 0.003899999999999998 hoop stress = 11115897.435897442 Pa
for thickness 0.003999999999999998 hoop stress = 10838000.000000004 Pa
for thickness 0.004099999999999999 hoop stress = 10573658.53658537 Pa
for thickness 0.004199999999999999 hoop stress = 10321904.761904765 Pa
for thickness 0.004299999999999999 hoop stress = 10081860.465116281 Pa
for thickness 0.004399999999999999 hoop stress = 9852727.272727273 Pa
for thickness 0.0045 hoop stress = 9633777.777777778 Pa
for thickness 0.0046 hoop stress = 9424347.826086957 Pa
for thickness 0.0047 hoop stress = 9223829.787234042 Pa
for thickness 0.0048000000000000004 hoop stress = 9031666.666666666 Pa
for thickness 0.004900000000000001 hoop stress = 8847346.93877551 Pa
for thickness 0.005000000000000001 hoop stress = 8670399.999999998 Pa
for thickness 0.005100000000000001 hoop stress = 8500392.156862743 Pa
for thickness 0.0052000000000000015 hoop stress = 8336923.076923074 Pa
for thickness 0.005300000000000002 hoop stress = 8179622.641509431 Pa
for thickness 0.005400000000000002 hoop stress = 8028148.1481481455 Pa
for thickness 0.005500000000000002 hoop stress = 7882181.818181815 Pa
for thickness 0.0056000000000000025 hoop stress = 7741428.571428568 Pa
for thickness 0.005700000000000003 hoop stress = 7605614.035087716 Pa
for thickness 0.005800000000000003 hoop stress = 7474482.758620686 Pa
for thickness 0.005900000000000003 hoop stress = 7347796.610169487 Pa
for thickness 0.006000000000000004 hoop stress = 7225333.333333329 Pa
for thickness 0.006100000000000004 hoop stress = 7106885.245901635 Pa
for thickness 0.006200000000000004 hoop stress = 6992258.064516124 Pa
for thickness 0.006300000000000004 hoop stress = 6881269.841269837 Pa
for thickness 0.006400000000000005 hoop stress = 6773749.999999995 Pa
for thickness 0.006500000000000005 hoop stress = 6669538.461538456 Pa
for thickness 0.006600000000000005 hoop stress = 6568484.848484843 Pa
for thickness 0.006700000000000005 hoop stress = 6470447.761194024 Pa
for thickness 0.006800000000000006 hoop stress = 6375294.117647054 Pa
for thickness 0.006900000000000006 hoop stress = 6282898.550724632 Pa
for thickness 0.007000000000000006 hoop stress = 6193142.857142852 Pa
for thickness 0.0071000000000000065 hoop stress = 6105915.492957741 Pa
for thickness 0.007200000000000007 hoop stress = 6021111.111111105 Pa
for thickness 0.007300000000000007 hoop stress = 5938630.136986296 Pa
for thickness 0.007400000000000007 hoop stress = 5858378.378378373 Pa
for thickness 0.0075000000000000075 hoop stress = 5780266.66666666 Pa
for thickness 0.007600000000000008 hoop stress = 5704210.526315784 Pa
for thickness 0.007700000000000008 hoop stress = 5630129.870129865 Pa
for thickness 0.007800000000000008 hoop stress = 5557948.717948712 Pa
for thickness 0.007900000000000008 hoop stress = 5487594.936708855 Pa
for thickness 0.008000000000000007 hoop stress = 5418999.999999995 Pa
for thickness 0.008100000000000007 hoop stress = 5352098.765432094 Pa
for thickness 0.008200000000000006 hoop stress = 5286829.268292679 Pa
for thickness 0.008300000000000005 hoop stress = 5223132.530120479 Pa
for thickness 0.008400000000000005 hoop stress = 5160952.380952378 Pa
for thickness 0.008500000000000004 hoop stress = 5100235.294117644 Pa
for thickness 0.008600000000000003 hoop stress = 5040930.232558138 Pa
for thickness 0.008700000000000003 hoop stress = 4982988.505747125 Pa
for thickness 0.008800000000000002 hoop stress = 4926363.636363635 Pa
for thickness 0.008900000000000002 hoop stress = 4871011.235955055 Pa
for thickness 0.009000000000000001 hoop stress = 4816888.888888888 Pa
for thickness 0.0091 hoop stress = 4763956.043956044 Pa
for thickness 0.0092 hoop stress = 4712173.9130434785 Pa
for thickness 0.0093 hoop stress = 4661505.376344087 Pa
for thickness 0.009399999999999999 hoop stress = 4611914.893617022 Pa
for thickness 0.009499999999999998 hoop stress = 4563368.421052633 Pa
for thickness 0.009599999999999997 hoop stress = 4515833.333333335 Pa
for thickness 0.009699999999999997 hoop stress = 4469278.350515465 Pa
for thickness 0.009799999999999996 hoop stress = 4423673.469387757 Pa
for thickness 0.009899999999999996 hoop stress = 4378989.898989901 Pa
for thickness 0.009999999999999995 hoop stress = 4335200.000000002 Pa
for thickness 0.010099999999999994 hoop stress = 4292277.227722774 Pa
for thickness 0.010199999999999994 hoop stress = 4250196.078431375 Pa
for thickness 0.010299999999999993 hoop stress = 4208932.038834955 Pa
for thickness 0.010399999999999993 hoop stress = 4168461.5384615413 Pa
for thickness 0.010499999999999992 hoop stress = 4128761.904761908 Pa
for thickness 0.010599999999999991 hoop stress = 4089811.3207547204 Pa
for thickness 0.01069999999999999 hoop stress = 4051588.7850467325 Pa
for thickness 0.01079999999999999 hoop stress = 4014074.074074078 Pa
for thickness 0.01089999999999999 hoop stress = 3977247.706422022 Pa
for thickness 0.010999999999999989 hoop stress = 3941090.909090913 Pa

Budget Constraints

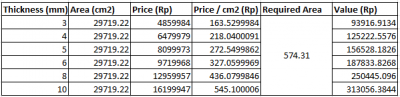
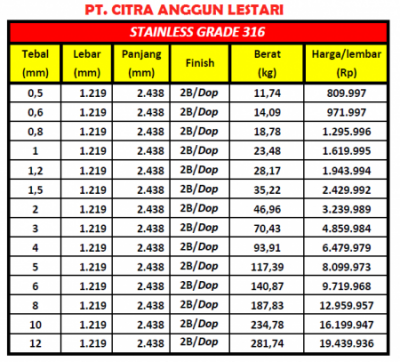
in order to meet the budget limitation of Rp500.000,-, it is necessary to assess the chosen geometric parameters. Given that the vessel is small and has thin walls, it is likely to be manufactured using sheet-metal fabrication. Therefore, the materials needed will be acquired in the form of sheet metal or plates.

The table provided above presents a narrowed-down selection of thickness ranges that fall within our area of interest. Since steel plates are not commonly available in small surface areas like the one required for our application, we have employed a cost per area analysis using data obtained from PT Citra Anggun Lestari. Similar to the situation with the strength constraint, all feasible thickness values result in material costs that are below our specified cost constraint. Therefore, in selecting the appropriate thickness, we must also consider the objective of minimizing weight while maintaining sufficient strength. Based on these considerations, we propose choosing a median wall thickness of 6 mm for the container.