Difference between revisions of "Irza Lutfi"
Irza Lutfi (talk | contribs) (→Progress 2 Tugas) |
Irza Lutfi (talk | contribs) (→Progress 2 Tugas) |
||
| Line 87: | Line 87: | ||
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah") | print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah") | ||
| − | [[File:Screenshot_2023-06-05_080206.png| | + | [[File:Screenshot_2023-06-05_080206.png|300x300px]] |
Revision as of 07:54, 5 June 2023
Introduction
Hallo Perkenalkan Saya Irza Lutfi Mahasiswa Teknik Mesin Universitas Indonesia Angkatan 2021 dengan NPM 2106638242!!
Metnum-01
Progress 1 Tugas
Untuk mengoptimalkan tangki hidrogen dengan kapasitas 1 liter dan tekanan 8 bar dengan biaya produksi maksimal Rp. 500.000, ada beberapa faktor yang perlu dipertimbangkan. Berikut adalah langkah-langkah yang dapat diambil untuk mencapai optimasi tersebut:
Material Tangki: Pertimbangkan material tangki yang efisien dan murah untuk digunakan dalam konstruksi tangki hidrogen. Pilihlah material yang memiliki kekuatan yang cukup untuk menahan tekanan 8 bar dan ringan agar tidak menambah berat tangki secara signifikan. Material yang mungkin dapat dipertimbangkan adalah aluminium atau serat karbon.
Desain Tangki: Rancanglah tangki dengan desain yang optimal untuk memaksimalkan kapasitas penyimpanan hidrogen dalam volume 1 liter. Bentuk silinder dengan diameter dan tinggi yang sesuai mungkin merupakan desain yang efisien untuk tujuan ini.
Efisiensi Pengisian: Perhatikan efisiensi pengisian tangki hidrogen. Pastikan sistem pengisian tangki meminimalkan kebocoran dan memastikan pengisian yang cepat dan efisien.
Pemilihan Komponen: Pilihlah komponen seperti katup pengisian, katup pengeluaran, dan sensor tekanan yang efisien dan ekonomis. Pastikan bahwa komponen tersebut memiliki kualitas yang baik agar dapat bekerja secara efektif dan aman.
Proses Produksi: Rancang proses produksi yang efisien untuk meminimalkan biaya produksi. Gunakan metode dan teknologi yang tepat untuk mempercepat produksi dan mengurangi biaya tenaga kerja.
Analisis Biaya: Lakukan analisis biaya mendalam untuk memastikan bahwa biaya produksi tetap di bawah batas maksimal Rp. 500.000. Tinjau biaya bahan baku, biaya tenaga kerja, biaya mesin, dan komponen lainnya yang terlibat dalam produksi tangki hidrogen. Identifikasi area-area di mana penghematan biaya dapat dicapai tanpa mengorbankan kualitas dan keamanan produk.
Optimalisasi Iteratif: Lakukan iterasi dan perbaikan berkelanjutan dalam desain dan proses produksi untuk mencapai hasil yang optimal. Tinjau kembali setiap langkah di atas dan identifikasi cara-cara untuk meningkatkan efisiensi dan mengurangi biaya.
Dengan mengikuti langkah-langkah di atas, diharapkan Anda dapat mengoptimalkan tangki hidrogen dengan kapasitas 1 liter, tekanan 8 bar, dan biaya produksi maksimal Rp. 500.000. Namun, perlu diingat bahwa optimasi ini hanya memberikan panduan umum, dan dapat diperlukan penyesuaian yang lebih rinci tergantung pada kebutuhan dan sumber daya yang tersedia.
Progress 2 Tugas
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen = 1
# Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x
# Kendala
def kendala(anggaran):
return budget_maksimal - (harga_per_unit * anggaran)
kendala_anggaran = {'type': 'ineq', 'fun': kendala}
# Nilai awal
x0 = 0
# Batasan
batas = [(0, None)]
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran])
# Menampilkan hasil
print("Status:", solusi.success and "Optimal" or "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
The code above uses the objective function to maximize the number of hydrogen storage units to buy. The budget constraint is set using the constraint function, which ensures that the total cost does not exceed the given maximum budget. The output will display the number of units that must be purchased, the total storage capacity, and the total cost required.
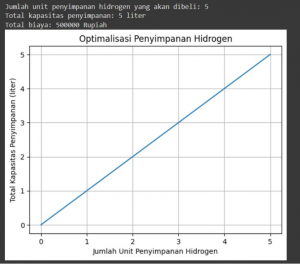
Code that shows us a graph of hydrogen storage optimization taking into account the given capacity and budget constraints.
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen
kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x * kapasitas_per_unit
# Kendala
def kendala(anggaran):
return budget_maksimal - (harga_per_unit * anggaran)
kendala_anggaran = {'type': 'ineq', 'fun': kendala}
# Nilai awal
x0 = 0
# Batasan
batas = [(0, None)]
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran])
# Menampilkan hasil
print("Status:", solusi.success and "Optimal" or "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")