Muhammad Alif Kurniawan

Introduction

Hello, nice to meet all of you and welcome to my page

My name is Muhammad Alif Kurniawan with NPM 2106732853

You can ask anything, lets going forward together

Definition of Hydrogen Tank

First of all, we will discuss a simple definition of a hydrogen tank, we can make a brief explanation about a hydrogen tank as follows :

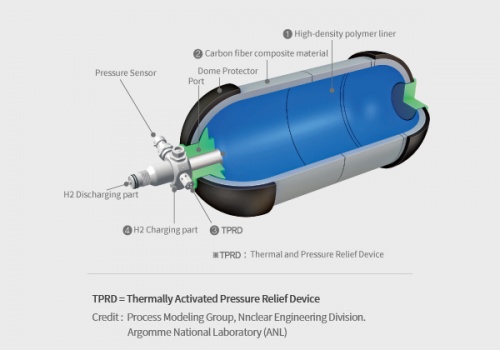
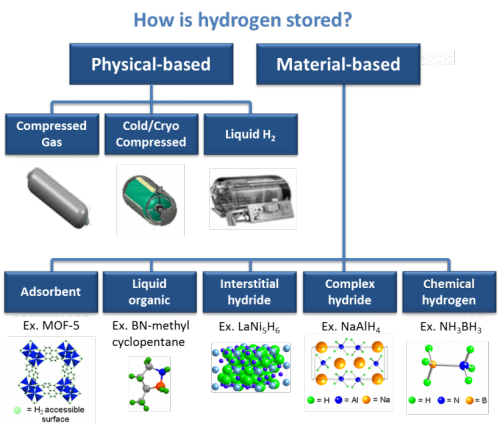
A hydrogen tank is a specialized container designed to store hydrogen gas, either under high pressure or as a cryogenic liquid, for various applications such as fuel cell vehicles, power generation, and industrial processes. The tank's primary function is to safely store hydrogen until it is needed and then release it for use in the desired application. It is constructed using high-strength materials to withstand the pressure or low-temperature conditions required for hydrogen storage. The tank may incorporate safety features, insulation (in the case of cryogenic tanks), and fittings or valves for filling and dispensing hydrogen.

After that, based on the assignment given on May 22, 2023. Every students are assigned to make an optimal design design for a hydrogen tank, for for the specifications that are used as constant variables in the production of hydrogen tanks can be seen below :

1. Has a capacity of 1 Liter

2. Operates at a pressure of 8 bar

3. Have a maximum production price of Rp. 500,000

Functionality of hydrogen Tank

Hydrogen tanks have been used in various ways, be it in everyday life or for other purposes, be it small scale to industrial scale. Here are the three main functionalities of a hydrogen tank:

A. Storage and Transport

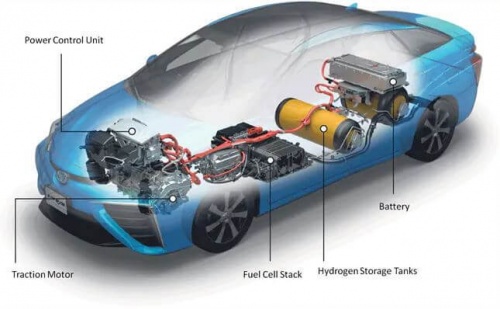
The main function of a hydrogen tank is to store and transport hydrogen gas safely. These tanks allow for the storage of significant amounts of hydrogen for use in applications such as fuel cell vehicles, power generation and industrial processes. By storing a sufficient amount of hydrogen, tanks allow efficient transportation from one location to another, allowing access to renewable energy sources in certain places.

B. Clean Energy Source

Hydrogen is a clean energy source and can be used to reduce greenhouse gas emissions and air pollution. By using a hydrogen tank, energy stored in the form of hydrogen can be released and used to generate electricity via fuel cells, drive fuel cell vehicles, or meet industrial energy needs. Hydrogen tanks play an important role in providing access to an environmentally friendly and sustainable source of energy.

C. Integration with Energy Infrastructure

Hydrogen tanks also work within the integration of a wider energy infrastructure. They can be connected to a hydrogen dispensing system which enables efficient refueling of fuel cell vehicles. In addition, hydrogen tanks can be integrated with existing energy storage networks and natural gas networks to provide energy reserves, offset fluctuations in supply and demand, and strengthen the stability of the energy system.

All in all, hydrogen tanks play an important role in storing, transporting and using hydrogen as a source of clean energy. They enable broader and more efficient access to hydrogen, assist in reducing emissions and support the transition to a low-carbon economy.

Advantages & Disadvantages of Hydrogen Tank

The use of hydrogen tanks as a fuel storage method certainly has some advantages and disadvantages. Here are some factors that can be considered in the hydrogen tank production process :

ADVANTAGES

1. Energy Sustainability

Hydrogen tanks allow for sustainable energy storage. Hydrogen can be produced from renewable energy sources, such as solar or wind power, through the electrolysis of water. By storing the generated energy in the form of hydrogen, the tank allows long-term storage and use of renewable energy when needed. This helps overcome the challenges of fluctuating energy supply and demand and enables the wider use of renewable energy.

2. High Energy Capacity

Hydrogen tanks have a very high energy capacity compared to conventional batteries. Relatively lighter in weight, a hydrogen tank can store more energy than a battery of the same capacity. This allows fuel cell vehicles to have a wider range and faster refueling times. In addition, the high energy capacity of hydrogen tanks also allows energy storage and use on a larger industrial scale.

3. Fast Charging Time

Filling a hydrogen tank can be done in a relatively short time. Compared to charging an electric battery which requires a longer time, filling a hydrogen tank can be comparable to filling a conventional fuel. This allows the use of fuel cell vehicles that are more comfortable and similar to fossil fuel vehicles. This fast charging time also contributes to efficiency and convenience in the use of hydrogen energy.

With energy sustainability, high energy capacity and fast filling times, hydrogen tanks are an attractive solution for energy storage and the use of hydrogen as a clean fuel. These advantages are helping to drive the adoption of hydrogen as a promising alternative in the transition to a more sustainable energy system.

DISADVANTAGES

1. High Pressure or Temperature

Hydrogen tanks used to store hydrogen in gaseous form usually require high pressure, reaching thousands of psi (pounds per square inch) to store sizable quantities. This requires a robust and high pressure resistant tank design, and creates a safety risk that must be managed with care. On the other hand, hydrogen tanks that store hydrogen as a cryogenic liquid require extremely low temperatures, below -253 degrees Celsius (-423 degrees Fahrenheit), which require additional insulation and infrastructure to maintain those low temperatures. Both of these can pose significant technical and cost challenges.

2. Storage Disadvantages

Although the energy capacity of hydrogen in a tank can be high, the energy stored in hydrogen has a disadvantage in terms of volume. Hydrogen has a low energy density when compared to fossil fuels such as gasoline or diesel. This means the hydrogen tank must be larger in size or heavier in order to store the same amount of energy compared to conventional fuels. Storage space-consuming can be a challenge in some applications, such as vehicles, where limited space is an important consideration.

3. Limited Infrastructure

Infrastructure for the production, storage and distribution of hydrogen is still limited and not fully developed as widely as fossil fuel infrastructure. This means limited access to hydrogen filling stations, lack of a distribution network, and lack of hydrogen production facilities can all become barriers to wider adoption of hydrogen-based technologies. Developing the infrastructure needed to support hydrogen tanks requires a large investment and takes a long time.

While hydrogen tanks have the advantage of being a sustainable energy storage, they also have some disadvantages that need to be addressed to drive wider adoption. Research and development is ongoing to address these challenges and improve the efficiency, safety and infrastructure associated with hydrogen tanks.

Mass Calculation

Hydrogen at a pressure of 8 bar has a boiling temperature of around -253.16°, therefore to be stable in liquid conditions a hydrogen tank with a lower temperature is needed By using the ideal gas law equation on known data such as a volume of 1 liter, a pressure of 8 bar, and a temperature of -253.16°C, the following results are obtained:

PV = nRT

Where:

P = pressure in Pa (Pascal)

V = volume in m³ (cubic meter)

n = number of moles of gas

R = ideal gas constant (8.314 J/(mol K))

T = temperature in Kelvin units

However, first we need to convert the temperature from -253.16°C to Kelvin units. To convert the temperature in degrees Celsius to Kelvin, we need to add 273.15.

So, the temperature of -253.16°C in Kelvin is: T = -253.16°C + 273.15 = 19.99 K

In this case, we need to find the number of moles of gas (n) in the tank. For that, we need to convert the pressure from 8 bar to Pascal units.

1 bar = 100,000 Pa

So, pressure 8 bar = 8 × 100,000 Pa = 800,000 Pa

Now we can combine all the values into the ideal gas law equation and find the number of moles of gas (n).

PV = nRT

(800,000 Pa) × (0.001 m³) = n × (8.314 J/(mol K)) × (19.99 K)

800,000 Pa × 0.001 m³ = n × 8.314 J/K × 19.99 K

800 J = n × 166.19686 J

n = 0.8 J / 166.19686 J

n = 4.81357 moles

So, with a volume of 1 liter, a pressure of 8 bar, and a temperature of -253.16°C, the estimated number of moles of hydrogen gas in the tank is about 4.81357 moles.

Then, to convert the number of moles of hydrogen (H2) to kilograms, we need to use the molar mass of hydrogen. The molar mass of hydrogen is about 2.016 grams/mol. So, to convert the number of moles of hydrogen to kilograms:

Number of moles of hydrogen = 4.81357 moles

The molar mass of hydrogen = 2.016 g/mol

Mass of hydrogen = Number of moles of hydrogen × Molar mass of hydrogen

= 4.81357 mol × 2.016 g/mol

= 9.70415 g

= 0.0097 kg

So, using the previous mole figures, the total mass of hydrogen in a tank with a volume of 1 liter, a pressure of 8 bar, and a temperature of -253.16°C is about 0.0097 kilograms.

Dimension Calculation

To get the dimensions of a hydrogen tank that can accommodate hydrogen gas as much as possible and use as little material as possible, there are calculations that need to be done Using calculus and numerical methods, we will find out the dimensions of a hydrogen tank that has the maximum volume and minimum surface area by using the cylinder volume equation as follows:

Volume = πr²h

V = πr²h

V/(πr²) = h

Then combining it with the equation for the surface area of the tube will get a new equation form, namely :

Surface Area = 2πr² + 2πrh

A = 2πr² + 2πrh

A = 2πr² + 2πr(V/(πr²))

A = 2πr² + 2V/r

Now, we need to find the minimum value of the surface area formula. We can use calculus to find the first and second derivatives of the formula.

d(A)/dr = 4πr - 2V/r²

d²(A)/dr² = 4π + 4V/r³

To find the minimum, we look for the point where the first derivative equals zero and the second derivative is positive (to confirm that it is a minimum value).

4πr - 2V/r² = 0

4πr = 2V/r²

2πr³ = V

To be sure, if we plug in the values we already got in the second derivative equation we will get the following values

d²(A)/dr² = 4π + 4V/r³

d²(A)/dr² = 4π + 4(2πr³)/r³

d²(A)/dr² = 4π + 8π

d²(A)/dr² = 12π (PROVEN POSITIVE)

To determine the relationship between the radius (r) and the height (h), we can use the initial volume equation

h = V/(πr²)

h = 2πr³/(πr²)

h = 2r