Difference between revisions of "Dzakiyya Yumna Fitrasani"
(→Hydrogen Storage Design, Optimization, and Calculation) |
(→Hydrogen Storage Design, Optimization, and Calculation) |
||
| Line 30: | Line 30: | ||
Storing hydrogen in gaseous form requires two main components – a storage compartment and a compressor to achieve higher storage pressure and increase the storage density. Gaseous hydrogen is usually not stored in pressure exceeding 100 bar in vessels above ground and 200 bar for underground storage (Wolf, 2015). The low density of hydrogen leads to the requirement of large storage volumes, and as a consequence, usually large investment costs. However, higher pressure e.g. 700 bar requires advanced vessel materials such as carbon fiber, which makes it very expensive and not considered viable for large-scale applications (Andersson & Grönkvist, 2019). One of the main advantages of storing hydrogen as compressed gas compared to liquid hydrogen is that most applications for hydrogen today require hydrogen in gaseous form. | Storing hydrogen in gaseous form requires two main components – a storage compartment and a compressor to achieve higher storage pressure and increase the storage density. Gaseous hydrogen is usually not stored in pressure exceeding 100 bar in vessels above ground and 200 bar for underground storage (Wolf, 2015). The low density of hydrogen leads to the requirement of large storage volumes, and as a consequence, usually large investment costs. However, higher pressure e.g. 700 bar requires advanced vessel materials such as carbon fiber, which makes it very expensive and not considered viable for large-scale applications (Andersson & Grönkvist, 2019). One of the main advantages of storing hydrogen as compressed gas compared to liquid hydrogen is that most applications for hydrogen today require hydrogen in gaseous form. | ||
| − | [[File:Hidrogen_satu.png| | + | [[File:Hidrogen_satu.png|500px|thumb|center|Fig. 1 – Components of a pressurized hydrogen storage tank.]] |
| Line 63: | Line 63: | ||
The fiber-resin composite, with 60% fiber by volume, has a manufactured-listed tensile strength of 2550 MPa. | The fiber-resin composite, with 60% fiber by volume, has a manufactured-listed tensile strength of 2550 MPa. | ||
| − | [[File:Schematic.png| | + | [[File:Schematic.png|500px|thumb|center|Fig. 2 – Schematic of compressed hydrogen storage tank (Roh et al., 2013).]] |
Fig. 2 shows a schematic drawing of a storage tank that is 1400 mm in length and 465 mm in diameter, which can store 5.6 kg of usable hydrogen (5.8 kg total) at 70 MPa. A fiber winding angle of 15 was used for the helical layers, while angles close to 90 were used for the hoop layers. To help squeeze out excessive resin during the winding process, the helical and hoop layers were wound alternately over the liner. | Fig. 2 shows a schematic drawing of a storage tank that is 1400 mm in length and 465 mm in diameter, which can store 5.6 kg of usable hydrogen (5.8 kg total) at 70 MPa. A fiber winding angle of 15 was used for the helical layers, while angles close to 90 were used for the hoop layers. To help squeeze out excessive resin during the winding process, the helical and hoop layers were wound alternately over the liner. | ||
| Line 82: | Line 82: | ||
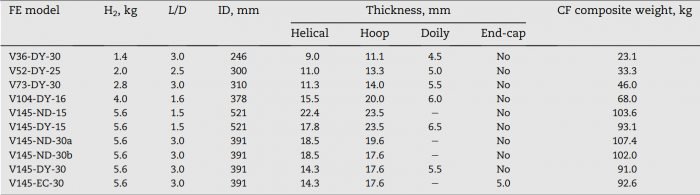
Tanks that fit within the available space onboard a vehicle typically have length-to-diameter ratio between ~1.5 and ~4.0. The results of the analysis showed only a small difference in the amount of composite needed, 103.6 kg for L/D of 1.5 versus 102.0 kg for L/D of 3.0. | Tanks that fit within the available space onboard a vehicle typically have length-to-diameter ratio between ~1.5 and ~4.0. The results of the analysis showed only a small difference in the amount of composite needed, 103.6 kg for L/D of 1.5 versus 102.0 kg for L/D of 3.0. | ||
| − | [[File:L-D Table.png| | + | [[File:L-D Table.png|700px|thumb|center|Table 1 – Geometry and weight of the composite for different models (Roh et al., 2013).]] |
Revision as of 17:18, 4 June 2023
Contents
Introduction
Hello, my name is Dzakiyya. I am a student in Metode Numerik-01. This will be my page regarding Metode Numerik.
FULLNAME: Dzakiyya Yumna Fitrasani
STUDENT NUMBER: 2106728055
Numerical Methods in Mechanical Engineering / 22 May 2023
Numerical methods are extensively used in various areas of mechanical engineering to solve complex mathematical equations, simulate physical phenomena, and optimize designs. Here are some key applications of numerical methods in mechanical engineering:
1. Solving Equations: Numerical methods such as root-finding algorithms (e.g., Newton-Raphson method) and numerical integration techniques (e.g., Simpson's rule, trapezoidal rule) are used to solve equations encountered in mechanical engineering, such as finding the roots of nonlinear equations or evaluating integrals in engineering analysis.
2. Finite Element Analysis (FEA): FEA is widely used in mechanical engineering for structural analysis. It involves dividing a complex structure into smaller finite elements and solving the equations of equilibrium numerically. FEA helps in determining stress, strain, deformation, and failure criteria in mechanical components and systems. It is used in the design and optimization of structures, such as buildings, bridges, and machine components.
3. Computational Fluid Dynamics (CFD): CFD is employed to analyze fluid flow and heat transfer in mechanical systems. Numerical methods, such as finite volume or finite element methods, are used to discretize the fluid domain and solve the governing equations (e.g., Navier-Stokes equations). CFD is applied in the design of aerodynamic profiles, HVAC systems, combustion chambers, and optimization of fluid flow in pipes and channels.
4. Optimization and Design: Numerical optimization techniques, such as genetic algorithms, gradient-based methods, and response surface methods, are employed to optimize designs in mechanical engineering. These methods help in finding optimal solutions for parameters like shape, size, material selection, and operating conditions, considering constraints and objective functions.
These are just a few examples of how numerical methods are applied in mechanical engineering. These methods enable engineers to solve complex problems, make informed design decisions, optimize performance, and reduce the need for costly physical experiments.
Hydrogen Storage Design, Optimization, and Calculation
A. Hydrogen Storage Technologies
Storing hydrogen in gaseous form requires two main components – a storage compartment and a compressor to achieve higher storage pressure and increase the storage density. Gaseous hydrogen is usually not stored in pressure exceeding 100 bar in vessels above ground and 200 bar for underground storage (Wolf, 2015). The low density of hydrogen leads to the requirement of large storage volumes, and as a consequence, usually large investment costs. However, higher pressure e.g. 700 bar requires advanced vessel materials such as carbon fiber, which makes it very expensive and not considered viable for large-scale applications (Andersson & Grönkvist, 2019). One of the main advantages of storing hydrogen as compressed gas compared to liquid hydrogen is that most applications for hydrogen today require hydrogen in gaseous form.
B. Aspects to be considered in designing hydrogen storage
When designing hydrogen storage systems, several aspects need to be considered to ensure safety, efficiency, and practicality. Here are some key factors to take into account:
1. Material Compatibility: Hydrogen can interact with various materials, leading to embrittlement or leakage. It is essential to select materials that are compatible with hydrogen and can withstand the operating conditions of the storage system. This includes considering factors such as material strength, corrosion resistance, and permeability to hydrogen.
2. Cost: The cost of the storage system plays a significant role in its viability. Design considerations should focus on optimizing cost-effectiveness while meeting the required storage capacity and safety standards.
3. Safety: Hydrogen is highly flammable and has a wide flammability range, so safety is of utmost importance. Storage systems must be designed to minimize the risk of leaks, explosions, and other hazards. Safety measures may include using robust materials, incorporating pressure relief devices, implementing proper ventilation, and ensuring effective leak detection systems.
4. Efficiency: The storage system should minimize energy losses during storage and retrieval processes. Any energy required for compression should be considered. Additionally, the system should minimize energy losses due to heat transfer or leakage.
5. Regulations and Standards: Compliance with relevant regulations, codes, and standards is crucial to ensure safety and performance. Design considerations should align with existing guidelines or actively contribute to the development of new standards as the hydrogen industry evolves.
C. Demands
Capacity: 1 liter
Pressure: 8 bar = 116 psi
Maximum budget: 500,000 IDR
D. Hydrogen storage specification based on demands
Material: carbon fiber
The fiber-resin composite, with 60% fiber by volume, has a manufactured-listed tensile strength of 2550 MPa.
Fig. 2 shows a schematic drawing of a storage tank that is 1400 mm in length and 465 mm in diameter, which can store 5.6 kg of usable hydrogen (5.8 kg total) at 70 MPa. A fiber winding angle of 15 was used for the helical layers, while angles close to 90 were used for the hoop layers. To help squeeze out excessive resin during the winding process, the helical and hoop layers were wound alternately over the liner.
E. Mathematical and numerical analysis
1. Netting analysis
Netting analysis is a preliminary sizing step to estimate the thicknesses of the helical and hoop layers for given pressure load, safety factor, and composite strength.
2. Hoop winding angle
The helical and hoop thicknesses are 18.5 mm and 19.6 mm, respectively. The total composite weight of the tank is 107.4 kg.
3. L/D ratio
Tanks that fit within the available space onboard a vehicle typically have length-to-diameter ratio between ~1.5 and ~4.0. The results of the analysis showed only a small difference in the amount of composite needed, 103.6 kg for L/D of 1.5 versus 102.0 kg for L/D of 3.0.
F. References
Roh, H. S., Hua, T. Q., & Ahluwalia, R. K. (2013). Optimization of carbon fiber usage in Type 4 hydrogen storage tanks for fuel cell automobiles. International Journal of Hydrogen Energy, 38(29), 12795–12802. https://doi.org/10.1016/j.ijhydene.2013.07.016
SAE TIR J2579Technical information report for fuel systems in fuel cell and other hydrogen vehicles. USA: Society of Automotive Engineers; 2008.