Difference between revisions of "Faizal Rikaz Al Muntaqo"
Rikazfaizal (talk | contribs) (→Pertemuan 6 (23/12/20)) |
Rikazfaizal (talk | contribs) (→Pertemuan 6 (23/12/20)) |
||
| Line 828: | Line 828: | ||
[[File:Tubes Metnum Faizal Rikaz A_4 Fixed Area.jpg|700px]] | [[File:Tubes Metnum Faizal Rikaz A_4 Fixed Area.jpg|700px]] | ||
| − | + | [[File:Tubes Metnum Faizal Rikaz A_6 Fixed Area.jpg|600px]] | |
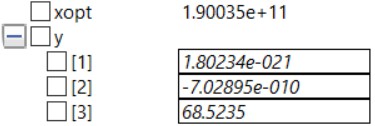
Dari hasil diatas dapat dilihat bahwa hasil yang paling optimum adalah SS316 dengan dimensi 30x30x3mm | Dari hasil diatas dapat dilihat bahwa hasil yang paling optimum adalah SS316 dengan dimensi 30x30x3mm | ||
Revision as of 17:43, 6 January 2021
Selamat Datang di laman Wiki saya!
Biodata
Nama : Faizal Rikaz Al Muntaqo
NPM : 1806201245
TTL : Jakarta, 15 Desember 1999
Hobi : Futsal
Saya adalah seorang mahasiswa Teknik Mesin UI angkatan 2018. Ketertarikan saya kepada Jurusan Teknik Mesin salah satunya didasari oleh rasa penasaran dan kesukaan saya terhadap teknologi yang terus berkembang tiap harinya dan dan juga tidak sedikit saya mendapatkan pengaruh secara tidak langsung dari ayah saya yang juga merupakan seorang Engineer. Saya sangat berharap nantinya ilmu ilmu yang telah saya dapatkan dari perkuliahan dapat diaplikasikan dikehidupan saya kedepannya dan semoga dapat berguna bagi keluarga, agama dan bangsa Indonesia.
Contents
Metode Numerik
Tujuan Pembelajaran
Tujuan pembelajaran dari mata kuliah Metode Numerik ini adalah:
- 1.Memahami konsep dan prinsip dasar dalam metode numerik (contoh:Persamaan aljabar, algorithma, dll)
- 2. Mengerti dan dapat mengaplikasikan aplikasi metode numerik
- 3. Mampu menerapkan ilmu-ilmu metode numerik dalam persoalan teknik
- 4. Mendapat nilai tambah adab sehingga dapat menjadi orang yang lebih beradab
Review Materi(Sebelum UTS)
Beberapa topik yang dibahas pada saat sebelum UTS meliputi:
- 1. Deret Taylor dan McLaurin
- 2. Regresi Linear
- 3. Interpolasi
- 4. Pseudocode
Pertemuan 1 (11/11/20)
Tugas Pertemuan 1 adalah mempelajari Modelica melalui situs Youtube lalu membuat video pembelajaran tentang Modelica kemudian di-upload di channel Youtube. Saya mempelajari Modelica melalui youtube pada situs berikut:
https://www.youtube.com/watch?v=m0Ahs8fEN28
Dan berikut merupakan Tugas video pembelajaran saya pada aplikasi modelica.
Pertemuan 2 (18/11/20)
Pada pertemuan kali ini kami sharing tugas yang telah diberikan diminggu lalu. Perbedaan Modelica dan Bahasa Coding lainnya (seperti: Phyton, dll) adalah modelica merupakan bahasa permodelan dan berbeda dengan bahasa coding sperti phyton dll. Pada proses simulate Open Modellica cukup lama karena proses dari bahasa modelica ke C lalu baru ke bahasa mesin. Namun ketika kita hanya merubah parameternya saja dengan cara me-resimulate maka proses akan cepat, karena tidak melewati proses perubahan bahasa lagi.
Mengapa menggunakan open modelica?
- - Cocok dengan engineer
- - Sistem perhitungan cepat
- - Banyak penggunanya
- - Free/ open technology
Tugas Video: https://www.youtube.com/watch?v=nVaCw_QBNaY
Pertemuan 3 (25/11/20)
Pada pertemuan ke 3 ini mempelajari tentang pseoudocode gauss elemination, lalu Pseudocode gauss dijelaskan oleh teman sekelas kami yaitu Christo. Lalu kami juga ditugaskan untuk membuat program sederhana menggunakan Open Modelica untuk menyelesaikan sebuah permasalahan yaitu mengenai Truss. Berikut Tugas Truss yang telah saya kerjakan.
TUGAS TRUSSES
class Tugas_Trusses parameter Integer N=8; //Global Matrice parameter Real A=0.001; //Area m2 parameter Real E=200e9; //Pa Real KG[N,N]; //global Real KGinitial[N,N]; //global Real Sol[N]; //global dispplacement Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; Real R[N]; Real SolMat[N,1]; Real XMat[N,1]; Real L1=1; Real L2=1; Real L3=1.6; Real L4=1.25; Real L5=1.6; Real Tetha1=degtorad(0); Real Tetha2=degtorad(0); Real Tetha3=degtorad(231.34); Real Tetha4=degtorad(270); Real Tetha5=degtorad(308.66); //Boundary condition Integer b1=1; Integer b2=3; //Truss 1 Real X1=Tetha1; Real k1=A*E/L1; Real K1[4,4]; //stiffness matrice Real KG1[N,N]; Integer p1o=1; Integer p1i=2; //Truss 2 Real X2=Tetha2; Real k2=A*E/L2; Real K2[4,4]; //stiffness matrice Real KG2[N,N]; Integer p2o=2; Integer p2i=3; //Truss 3 Real X3=Tetha1; Real k3=A*E/L3; Real K3[4,4]; //stiffness matrice Real KG3[N,N]; Integer p3o=2; Integer p3i=4; //Truss 4 Real X4=Tetha4; Real k4=A*E/L4; Real K4[4,4]; //stiffness matrice Real KG4[N,N]; Integer p4o=1; Integer p4i=4; //Truss 5 Real X5=Tetha5; Real k5=A*E/L5; Real K5[4,4]; //stiffness matrice Real KG5[N,N]; Integer p5o=3; Integer p5i=4; algorithm //Pembuatan Matrice Global K1:=Stiffness_Matrices(X1); KG1:=k1*Local_Global(K1,N,p1o,p1i); K2:=Stiffness_Matrices(X2); KG2:=k2*Local_Global(K2,N,p2o,p2i); K3:=Stiffness_Matrices(X3); KG3:=k3*Local_Global(K3,N,p3o,p3i); K4:=Stiffness_Matrices(X4); KG4:=k4*Local_Global(K4,N,p4o,p4i); K5:=Stiffness_Matrices(X5); KG5:=k5*Local_Global(K5,N,p5o,p5i); KG:=KG1+KG2+KG3+KG4+KG5; KGinitial:=KG; //Implementing Boundary Condition for i in 1:N loop KG[2*b1-1,i]:=0; KG[2*b1,i]:=0; KG[2*b2-1,i]:=0; KG[2*b2,i]:=0; end for; KG[2*b1-1,2*b1-1]:=1; KG[2*b1,2*b1]:=1; KG[2*b2-1,2*b2-1]:=1; KG[2*b2,2*b2]:=1; //Solving Displacement Sol:=Gauss_Jordan(N,KG,X); //Solving Reaction Force SolMat:=matrix(Sol); XMat:=matrix(X); R:=Reaction_Trusses(N,KGinitial,SolMat,XMat); end Tugas_Trusses;
Fungsi Degtorad
function Degtorad input Real deg; output Real rad; protected constant Real pi = 3.14; algorithm rad:=deg*pi/180; end Degtorad;
Fungsi Stiffness Matrices
function Stiffness_Matrices
input Real A;
output Real X[4,4];
protected
Real Y;
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-
Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-
(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),
(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),
(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
Fungsi Local Global
function Local_Global input Real Y[4,4]; input Integer B; input Integer p1; input Integer p2; output Real G[B,B]; algorithm for i in 1:B loop for j in 1:B loop G[i,j]:=0; end for; end for; G[2*p1,2*p1]:=Y[2,2]; G[2*p1-1,2*p1-1]:=Y[1,1]; G[2*p1,2*p1-1]:=Y[2,1]; G[2*p1-1,2*p1]:=Y[1,2]; G[2*p2,2*p2]:=Y[4,4]; G[2*p2-1,2*p2-1]:=Y[3,3]; G[2*p2,2*p2-1]:=Y[4,3]; G[2*p2-1,2*p2]:=Y[3,4]; G[2*p2,2*p1]:=Y[4,2]; G[2*p2-1,2*p1-1]:=Y[3,1]; G[2*p2,2*p1-1]:=Y[4,1]; G[2*p2-1,2*p1]:=Y[3,2]; G[2*p1,2*p2]:=Y[2,4]; G[2*p1-1,2*p2-1]:=Y[1,3]; G[2*p1,2*p2-1]:=Y[2,3]; G[2*p1-1,2*p2]:=Y[1,4]; end Local_Global;
Fungsi Reaction Trusses
function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; output Real Sol[N]; protected Real X[N,1]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses;
TUGAS GAUSS JORDAN
function Tugas_GaussJordan
input Real [:,:] A;
output Real [:,:] B;
protected // local variable
Integer h = 1; //pivot row
Integer k = 1; //pivot coloumn
Integer m = size(A,1); //Number of row
Integer n = size(A,2); //Number of column
Integer c = 0;
Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column;
Real [:] pivot_row;
Real [:,:] temp_array;
Real r;
Real float_error = 10e-10;
algorithm
//function input A and output B
B := A;
while h <= m and k <= n loop
for i in 1 : m loop
for j in 1 : n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
//Finding pivot
pivot_column:= {B[i,h] for i in h:m};
//Search for the bottom row that has the highest pivot value
c:=h-1;
for element in pivot_column loop
c:= c+1;
if abs(element)== max(abs(pivot_column)) then
max_row :=c;
end if;
end for;
//If there are no pivots in this column, move to the next column
if B[max_row,k] == 0 then
k:=k+1;
else
// switch row h - max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
//devide pivot row by pivot number
B[h] := B[h]/B[h,k];
for i in (h+1) :m loop
r := B[i,k]/B[h,k];
B[i,k]:=0;
for j in (k+1) : n loop
B[i,j] := B[i,j]-B[h,j] * r;
end for;
end for;
//move to pivot column and the next row
h := h+1;
k := k+1;
end if;
end while;
// from the top right
h :=m;
k :=n;
while h >=1 and k>=1 loop
//dealing with error
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <=float_error then
B[i,j]:=0;
end if;
end for;
end for;
//finding pivot
pivot_row := {B[h,i] for i in 1:k};
//Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k:= c;
// no pivot in this row, move to next row
if B[h,k] == 0 then
h:= h-1;
else
//perform row operatation
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] *r;
end for;
//move to next pivot row dan column
h:=h+1;
k:=k+1;
end if;
end while;
end Tugas_GaussJordan;
Pertemuan 4 (02/12/20)
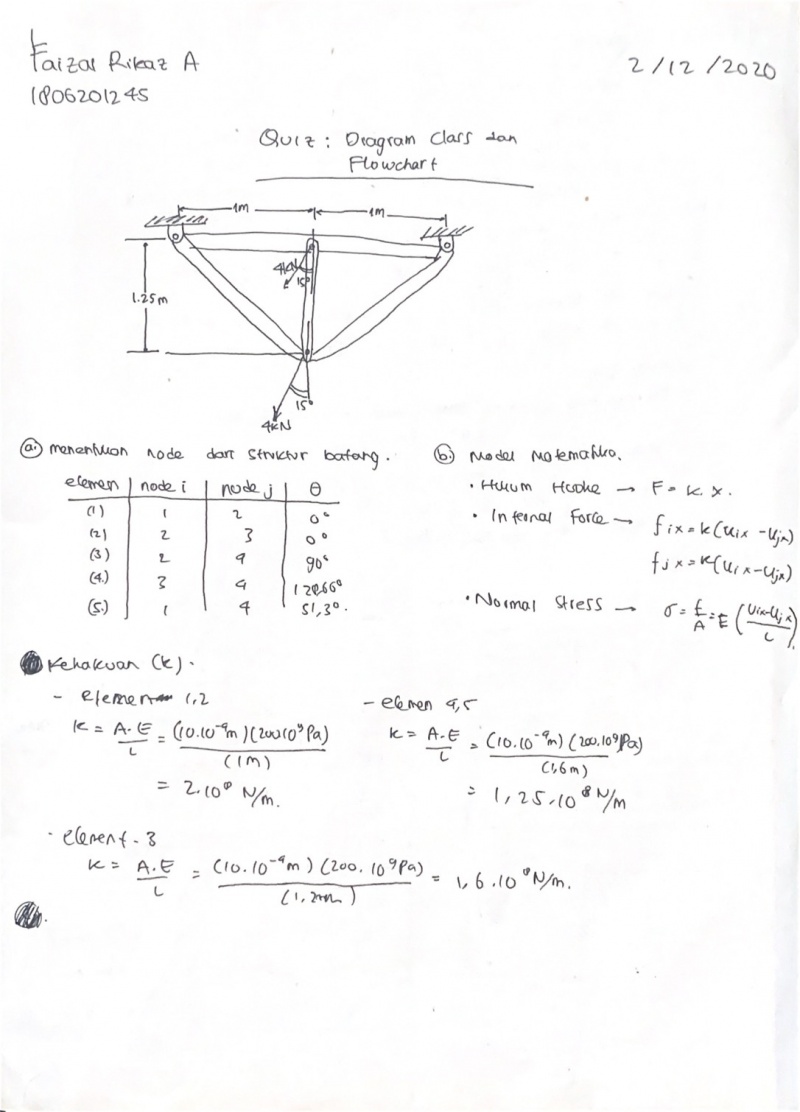
Membuat diagram class dan flowchart
QUIZ 1
Berikut jawaban beserta Flowchart dari QUIZ 1 saya.
TUGAS PERTEMUAN 4
Berikut merupakan jawaban dari Tugas Pertemuan 4 saya
Pertemuan 5 (16/12/20)
Pertemuan kali ini kami belajar melalui video yang diberikan Bu Chandra tentang aplikasi metode numerik dalam optimasi sebuah sistem menggunakan OpenModelica. Dibahas pula contoh dari optimasi menggunakan metode Bracket. Berikut pseudocode yang digunakan pada OpenModelica :
FungsiObjek.mo function FungsiObjek input Real x; output Real y; algorithm y:= 2*Modelica.Math.sin(x)-x^2/10; end FungsiObjek;
Fungsi panggil
BracketOptimal.mo
model BracketOptimal
parameter Integer n = 8;
Real x1[n];
Real x2[n];
Real xup;
Real xlow;
Real f1[n];
Real f2[n];
Real xopt;
Real yopt;
Real d;
algorithm
xup := 4;
xlow := 0;
for i in 1:n loop
d:=((5^(1/2)-1)/2) * (xup-xlow);
x1[i] := xlow+d;
x2[i] := xup-d;
f1[i] := FungsiObjek(x1[i]);
f2[i] := FungsiObjek(x2[i]);
if f1[i]>f2[i] then
xup := xup;
xlow := x2[i];
xopt := xup;
yopt := f1[i];
else
xlow :=xlow;
xup := x1[i];
xopt := xup;
end if;
end for;
end BracketOptimal;
Pertemuan 6 (23/12/20)
TUGAS BESAR
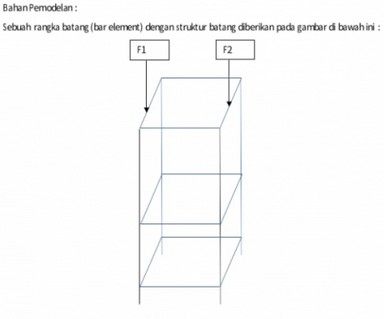
Pada pertemuan ke 6 ini kami diberi sebuah tugas besar yang dimana mahasiswa diharuskan mendesign suatu rangka dengan hasil yang terbaik namun juga memerhatikan cost agar mndapat harga yang relatif murah pula. Selain mempertimbangkan biaya serta material, area cross section truss pun juga ikut dipertimbangkan.
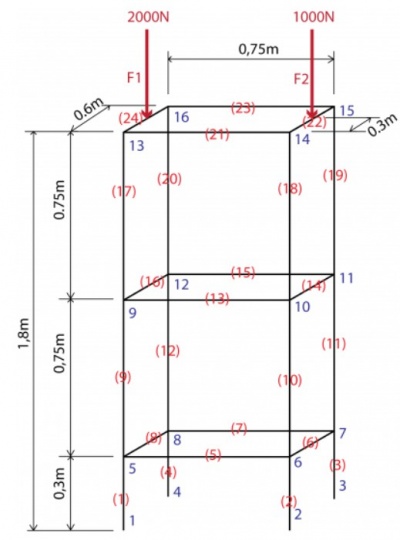
Pendefinisian
Berikut merupakan pendefinisian node dan elemen pada struktur batang.
Asumsi dan Constraint pada problem
Asumsi
- Material
- Luas permukaan truss
- Tidak adanya bending
- Beban terdistribusi di node - node
- Batas displacement 0,001m sebelum buckling
- Nilai safety factor 2
Constraint:
- Node 1, 2, 3, dan 4 fixed.
- Beban F1 dan F2 terdistribusi ke node sekitarnya
- Node 13 & 16 = 1000N
- Node 14 & 15 = 500N
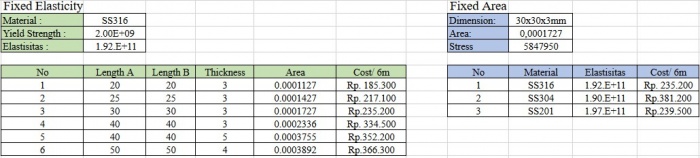
Data yang digunakan
Berikut merupakan dua metode pendekatan yang digunakan dalam pencarian dimensi area dan material teroptimal dalam pembentukan rangka.
Permodelan Numerik
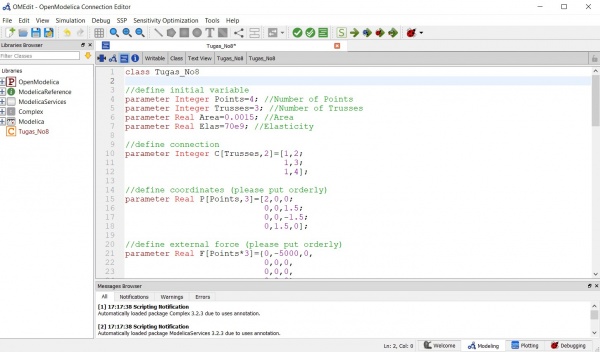
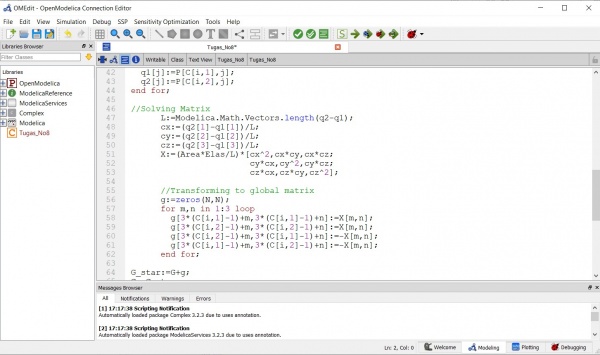
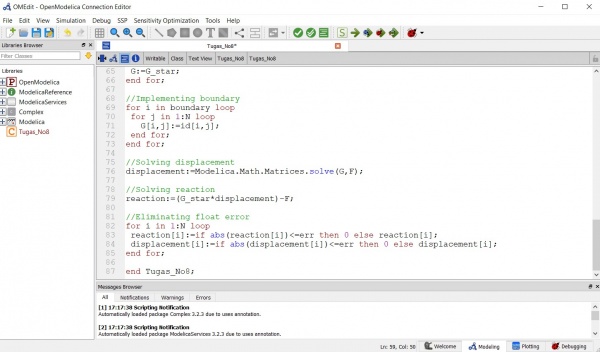
Berikut merupakan permodelan numerik dan komputasi pada Open Modelica
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=2.0e8; //Yield Strength (Pa)
parameter Real Area=0.0001727; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=192e11; //Elasticity SS 316 (Pa)
model TugasBesar_FaizalRikaz
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
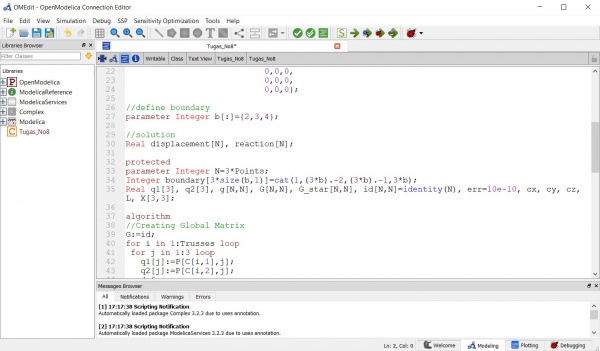
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
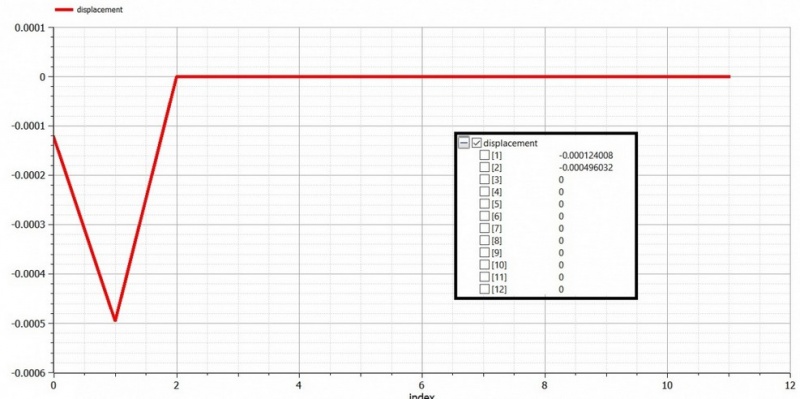
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
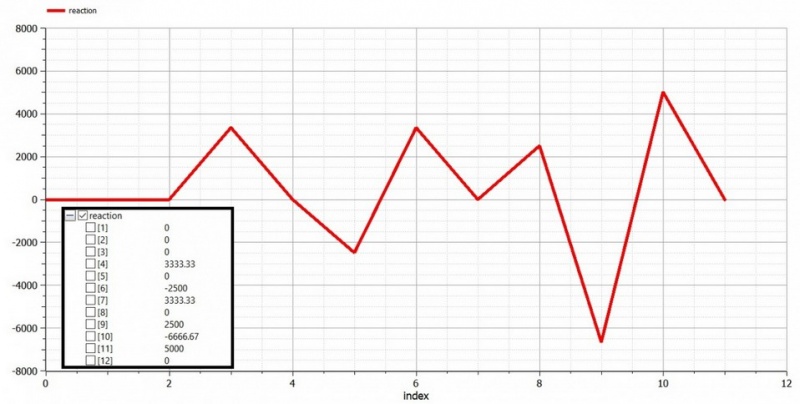
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end TugasBesar_FaizalRikaz;
Kurva Curve Fitting
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting;
Golden Section
model Opt_Gold
parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=87e-6;
parameter Real xhi=504e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
Hasil Perhitungan
- Fixed Elasticity
Berikut merupakan hasil perhitungan dengan fixed elasticity
Dan berikut merupakan grafik yang diperoleh dengan menggunakan metode Curve Fitting
Dari hasil diatas dapat dilihat bahwa hasil yang paling optimum adalah SS316 dengan dimensi 30x30x3mm
- Fixed Area
Berikut merupakan hasil perhitungan dengan fixed area
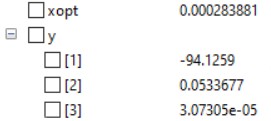
Dan berikut merupakan grafik yang diperoleh dengan menggunakan metode Curve Fitting
Dari hasil diatas dapat dilihat bahwa hasil yang paling optimum adalah SS316 dengan dimensi 30x30x3mm