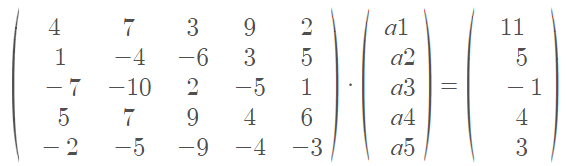Difference between revisions of "Muhammad Faridz Athaya"
| Line 844: | Line 844: | ||
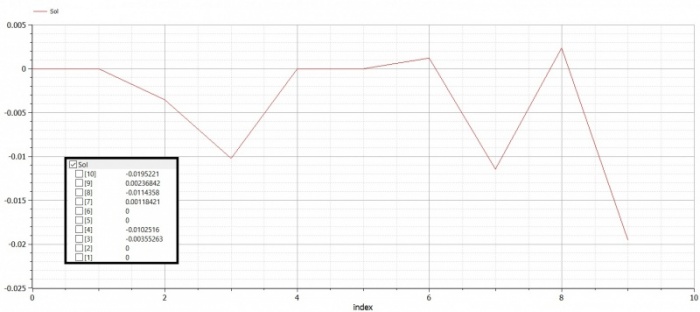
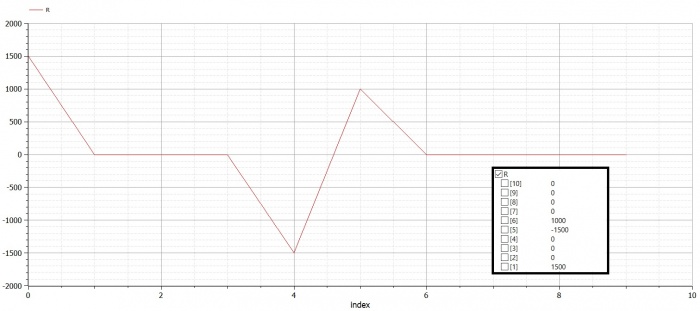
Maka didapatkan data | Maka didapatkan data | ||
[[File:Hasil Komputasi Elasticity Tetap.PNG|700px|thumb|center]] | [[File:Hasil Komputasi Elasticity Tetap.PNG|700px|thumb|center]] | ||
| + | |||
| + | Kemudian dilakukan Optimasi dengan menggunakan Golden Ratio yang kemudian didapatkan data | ||
| + | [[File:Screenshot (914).png|700px|thumb|center]] | ||
| + | |||
| + | '''Area Tetap''' | ||
| + | |||
| + | [[File:Area tetap.PNG|700px|thumb|center]] | ||
| + | [[File:Area tetappp.PNG|700px|thumb|center]] | ||
Revision as of 09:31, 6 January 2021
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ
Contents
Biodata
Nama : Muhammad Faridz Athaya
NPM : 1806149160
TTL : Jakarta, 12 Oktober 1999
Tempat Tinggal: Jatisampurna
Faridz merupakan mahasiswa semester 5 jurusan teknik mesin di Universitas Indonesia. Selama dua tahun di Universitas Indonesia, Faridz cukup aktif dalam berorganisasi di lingkup Fakultas Teknik. Dimana Faridz memiliki pengalaman organisasi di IMM FTUI dan BEM FTUI di tahun pertama, dan diamanahkan sebagai Ketua IMM FTUI di tahun ini hingga bulan desember nanti. Sebagai seorang mahasiswa, Faridz mempunyai mimpi untuk dapat menginspirasi banyak orang dan membawa kebaikan bagi lingkungannya. Oleh karena itu, Faridz selalu berusaha aktif dan memberikan manfaat lewat organisasi dan belajar dengan tekun agar ilmu yang dipelajari akan bermanfaat bagi agama, bangsa, dan negara di kemudian hari. Insha Allah dengan niat yang tulus dan semangat menebar kebaikan, apa yang diimpikan oleh Faridz akan tercapai
Sebelum UTS
Sebelum UTS kami diajarkan oleh Pak Dr. Ir. Engkos A. Kosasih, M. T., dimana materi yang diajarkan adalah
- Deret Mclaurin & Deret Taylor, dengan metode forward, center, dan backward
- Bracketing Methods dan Open Methods, dimana bracketing methods meliputi graphical methods, bisection methods, dan false-position methods sedangkan open methods meliputi simple fixed-point iteration, newton-raphson methods, secant methods, dan brents methods
- Mencari nilai interpolasi dan regresi linier menggunakan matriks
Minggu 1 (11 November 2020)
Pada pertemuan pertama, Pak Dr. Ir. Ahmad Indra Siswantara memperkenalkan kami dengan situs wiki air dan kami diarahkan juga untuk membuat page kami sendiri di situs tersebut. Dimana nantinya kami harus mengupdate dan mereview setiap pertemuan dengan Pak Dr. Ir. Ahmad Indra Siswantara, beliau juga memberi tahu kepada kami tujuan mempelajari Metode Numerik, yaitu untuk memahami konsep dan prinsip dasar metode numerik, mengerti bagaimana mengaplikasikannya, dan mampu menerapkannya pada persoalan yang berbau keteknikan
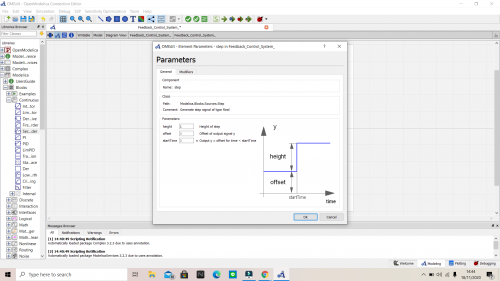
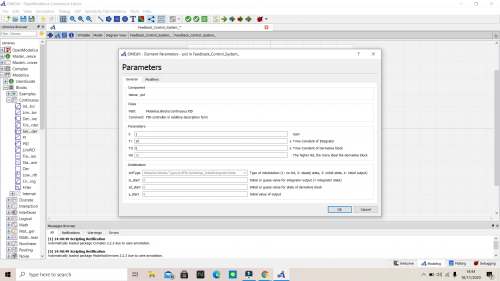
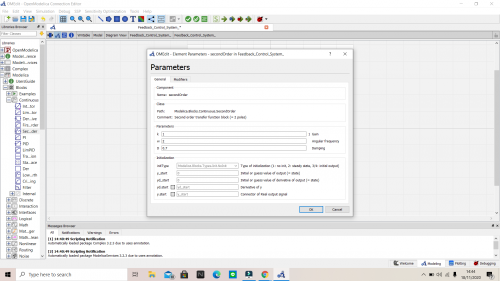
Setelah melaksanakan kelas metode numerik pada minggu pertama, kami diberikan tugas untuk membuat video tutorial mengenai pemakaian aplikasi OpenModelica pada suatu pekerjaan. Dimana saya akhirnya memilih untuk mengangkat video tutorial membuat Feedback Control System Sederhana dengan aplikasi OpenModelica sebagai tugas saya. Dalam membuat Feedback Control System Sederhana, saya menggunakan Step sebagai Sourcenya, Feedback, PID dan Second Order yang parameternya bisa dilihat pada gambar di bawah ini
Untuk penjelasan lebih lengkap, dapat dilihat video tutorial saya dalam membuat Feedback Control System Sederhana pada
Minggu 2 (18 November 2020)
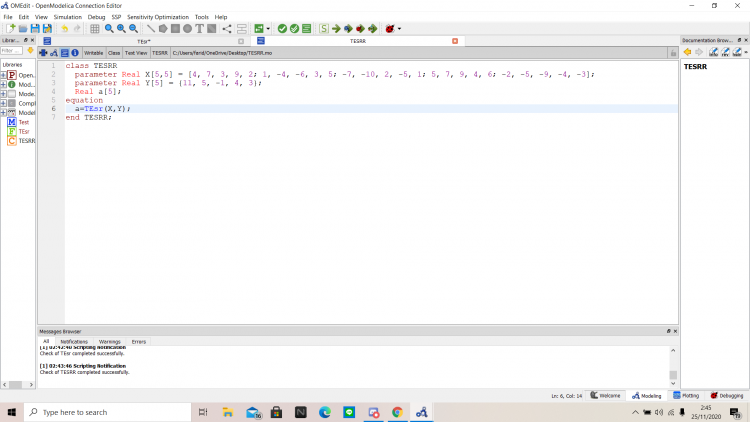
Dalam lebih mendalami materi yang sudah disampaikan di minggu kedua, saya menguji matriks 5x5 yang saya buat sendiri dan saya coba menyelesaikannya dengan OpenModelica, berikut matriks yang akan saya uji
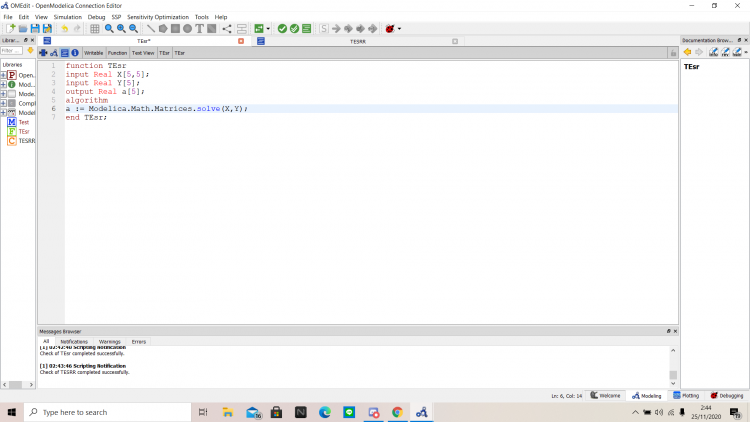
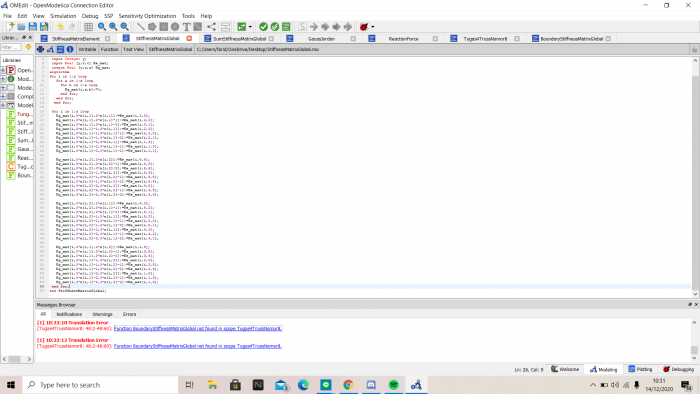
Disini saya menggunakan metode Gauss Elimination. OpenModelica memiliki function yang sudah tersedia untuk menyelesaikan matriks X*a = Y, dimana X merupakan matriks 5 x 5 pada ruas kiri persamaan, Y merupakan hasil dari persamaan yang berada pada ruas kanan persamaan, dan a merupakan nilai yang ingin dicari. Function yang tersedia ini bernama solve dan kita dapat menggunakannya dengan mengetik Modelica.Math.Matrices.solve pada algoritma. Untuk memudahkan eksekusi pada class, saya membuat function terlebih dahulu dengan X dan Y sebagai input serta a sebagai output.
Berikut merupakan class yang saya buat untuk mempermudah menyelesaikan permasalahan yang saya uji
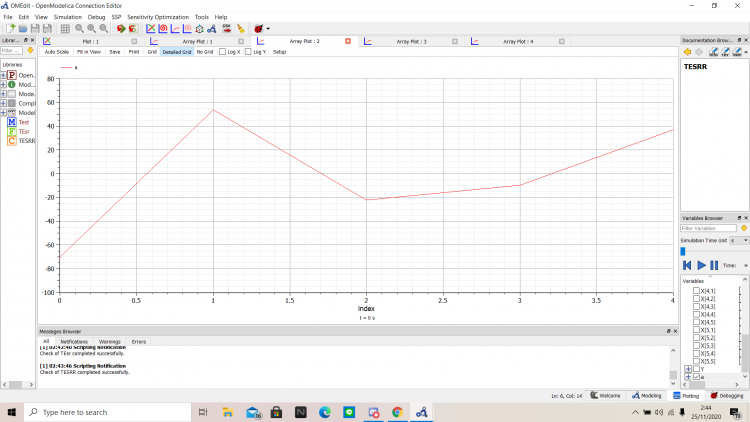
Setelah itu, saya mulai simulasikan fungsi yang sudah saya buat dengan memanggil class ke fungsi yang saya buat, sehingga didapatkan jawaban dengan membentuk grafik sebagai berikut
Dari grafik di atas, maka didapatkan nilai a masing-masing adalah:
- a1 = -70.358
- a2 = 53.333
- a3 = -22.368
- a4 = -9.9111
- a5 = 37.0032
Untuk lebih lengkapnya, dapat ditonton melalui video tutorial yang saya buat dan upload di youtube
Minggu 3 (25 November 2020)
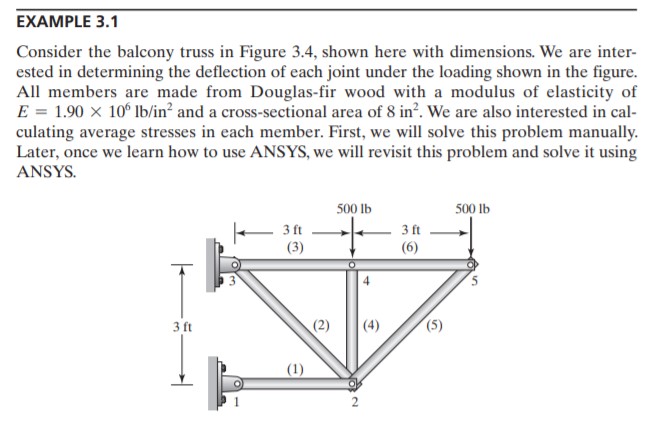
Tugas 1 (Example 3.1)
|
Persamaan model Trusses
parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary coundition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];
//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);
G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses;
|
Homework
|
Persamaan class Trusses_HW
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses_HW;
|
Fungsi Panggil
Matrice Transformation
function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
Global Element Matrice
function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
Reaction Matrice Equation
function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses;
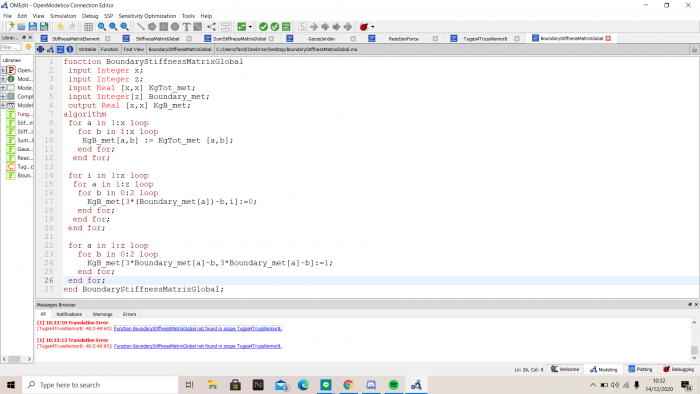
Minggu 4 (2 Desember 2020)
Kuis:
Membuat Flowchart untuk penyelesaian soal nomor 4
Tugas Minggu 4
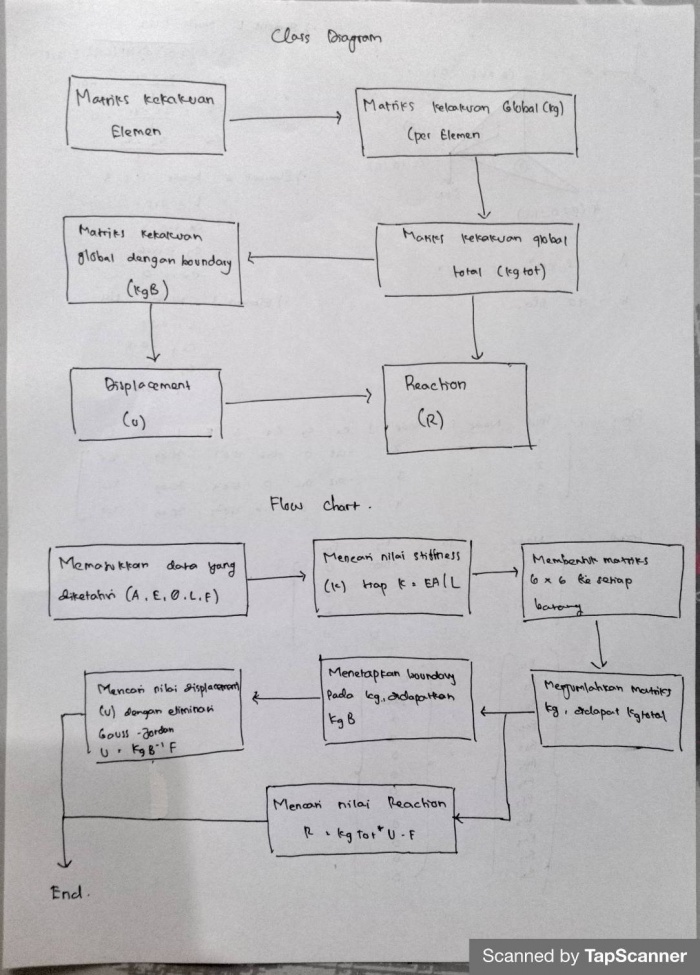
Dalam mengerjakan soal tersebut, saya pertama membuat flow chart dan class diagramnya terlebih dahulu
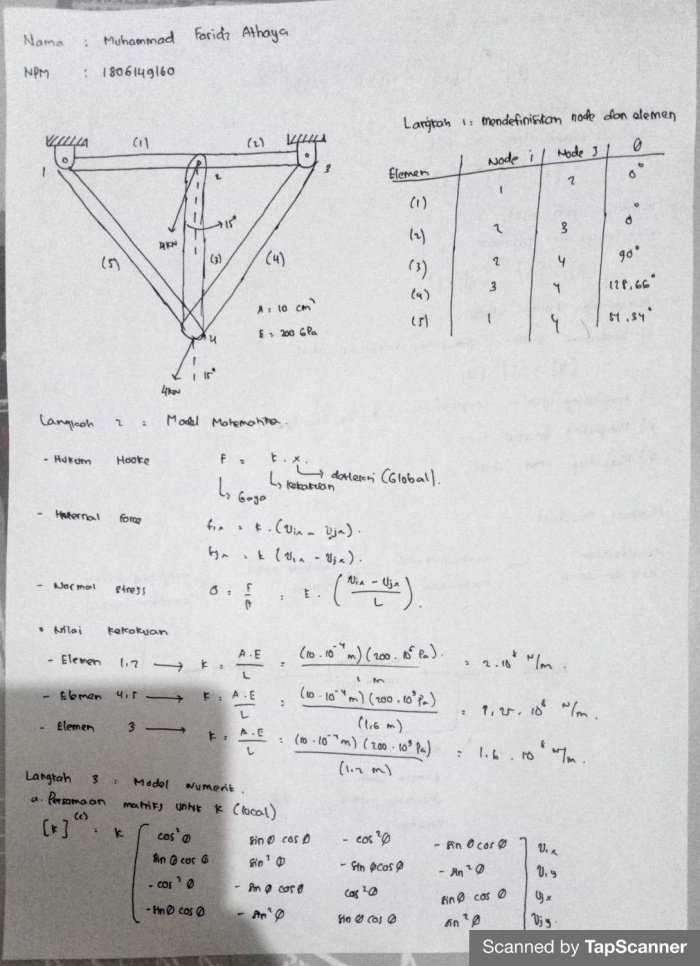
Kemudian, saya membuat FBD terlebih dahulu untuk mencari data-data yang diperlukan, yaitu node, sudut, luas, modulus elastisitas, dan panjang dari tiap batang yang nantinya akan menjadi data yang mempermudah saya dalam menyelesaikan permasalahannya lewat OpenModelica
Nilai k dapat didapatkan dengan rumus k=AE/L. Setelah mendapat nilai k setiap batang, nilai tersebut akan digunakan untuk membuat matriks K elemental (Ke) setiap batang.
Kemudian matriks 6x6 tersebut akan dibuat menjadi matriks 12x12 sesuai dengan jumlah batang (3) * jumlah node (4). Ini disebut matriks kekakuan global (Kg).
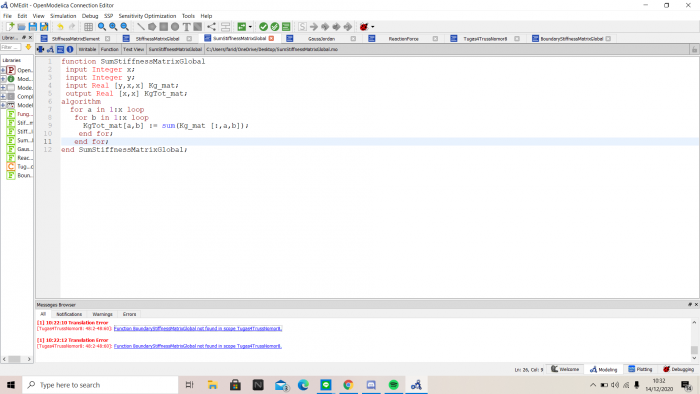
Kemudian untuk mendapatkan matriks kekakuan global total (KgTot), saya menjumlahkan matriks kekakuan global setiap batang
Pada soal ini, node 2,3, dan 4 merupakan pinned. Sehingga diberikan boundary pada matriks kekakuan global sebagai berikut U2X=U2Y=U2Z=U3X=U3Y=U3Z=U4X=U4Y=U4Z=0.
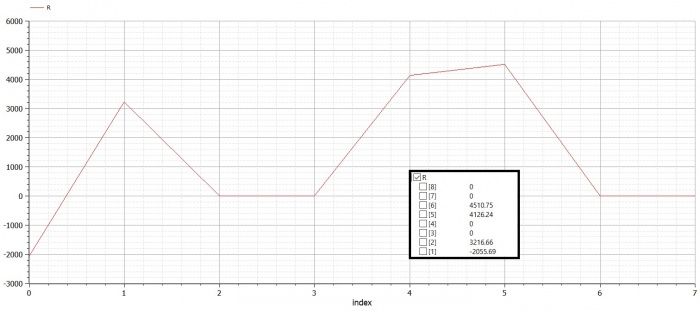
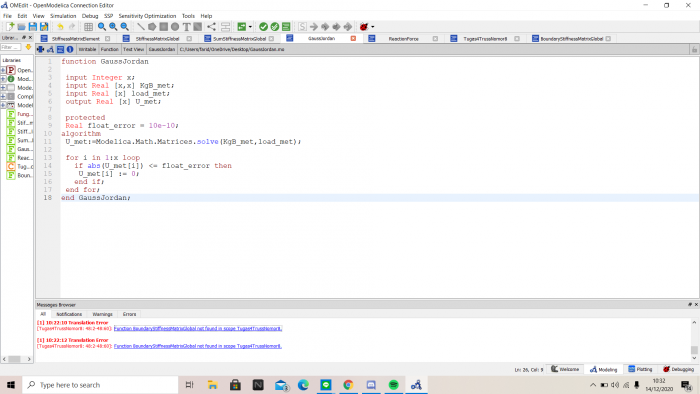
Untuk mencari displacement-nya digunakan gauss jordan untuk menyelesaikan matriks dengan F sebagai external load
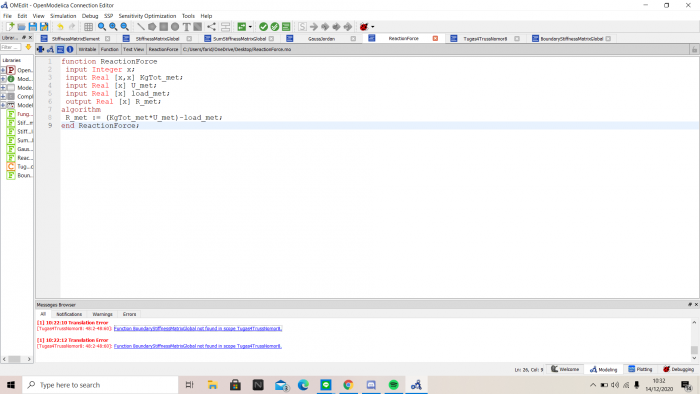
Sedangkan untuk mencari reaction menggunakan persamaan R=Kg*U - F.
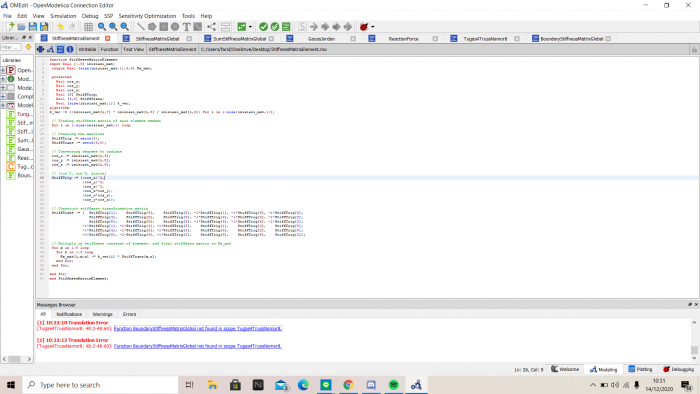
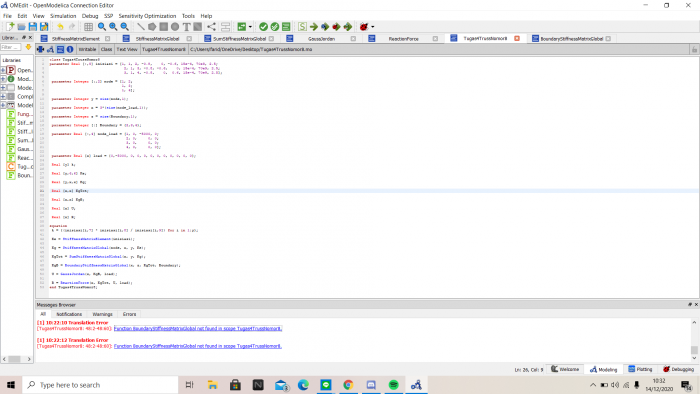
Setelah semua function telah dibuat, maka dibuat class
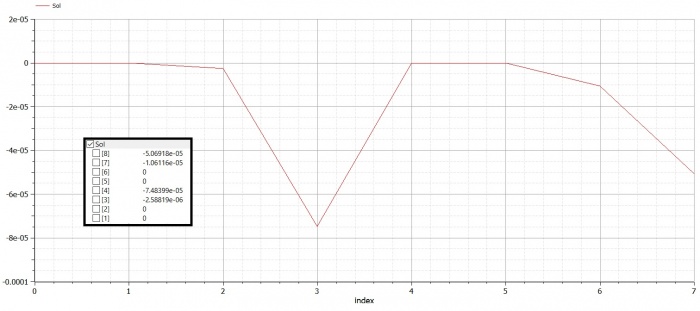
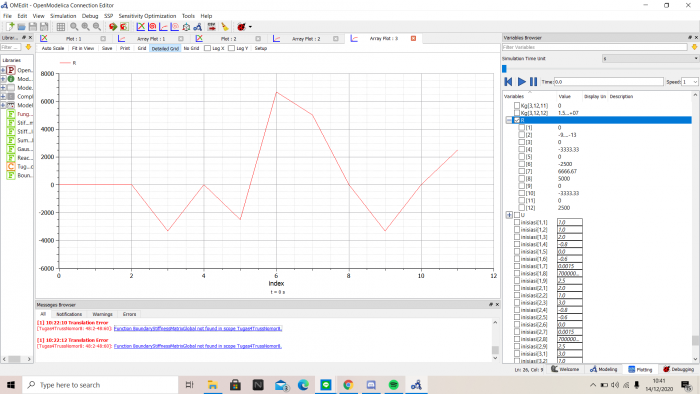
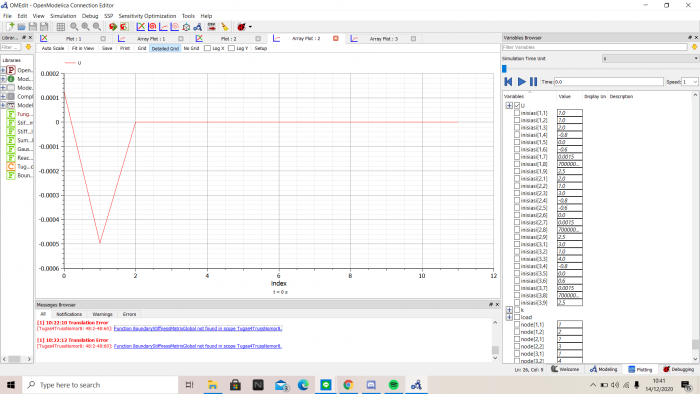
Setelah disimulasikan dihasilkan nilai Displacement (U) dan nilai R
Selengkapnya dapat dilihat dalam video berikut
Minggu 5
Pada pertemuan kelas pengganti, kami mereview ulang hal apa saja yang sudah kami terima dan serap selama perkuliahan Metode Numerik. Di kelas ini kami juga kembali mereview dan diajarkan tentang sistem trusses menggunakan OpenModelica dengan metode sharing dengan teman-teman yang mengerti.
Minggu 6 (16 Desember 2020)
Pada pertemuan minggu ke-6, kami diajarkan mengenai optimasi dengan menggunakan aplikasi OpenModelica. Optimasi merupakan cara untuk mendapatkan nilai minimum atau maksimum dari suatu permasalahan. Terdapat beberapa aspek yang diperhatikan dalam melakukan optimasi yaitu fungsi objektif dan ada juga konstrain. Pada kali ini Asisten Dosen yaitu Bu Chandra memberikan tutorial untuk melakukan optimasi menggunakan metode Bracket. Pada metode "Bracket Optimization Using Golden Ratio" terdapat satu graik yang mempunyai nilai f(x) global maks dan lokal maks serta terdapat f(x) global minimum dann lokal minimum. Pada pertemuan kali ini, Bu chandra mengajarkan sampai melakukan optimasi grafik tanpa sebuah konstrain.
Berikutnya kami diberikan contoh penggunaan optimasi pada OpenModelica sebagai berikut
Fungsi panggil
function f_obj3 import Modelica.Math; input Real x; output Real y; algorithm y:= 2*Math.sin(x)-x^2/10; end f_obj3;
setelah itu kita dapat membuat model optimasi sistem bracket sesuai yang diajarkan
model bracket_optimation3 parameter Integer n=8; Real x1[n]; Real x2[n]; Real xup; Real xlow; Real d; Real f1[n]; Real f2[n]; Real xopt; Real yopt; algorithm xup :=4; xlow:=0; for i in (1:n) loop d:= (5^(1/2)-1)/2*(xup-xlow); x1[i]:= xlow+d; x2[i]:= xup-d; f1[i]:= f_obj3(x1[i]); f2[i]:= f_obj3(x2[i]); if f1[i]>f2[i] then xup:= xup; xlow:= x2[i]; xopt:= xup; yopt:= f1[i]; else xlow:= xlow; xup:= x1[i]; xopt:= xup; end if; end for; end bracket_optimation3;
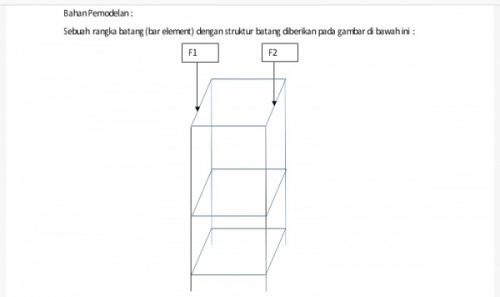
Tugas Besar: Aplikasi Numerik dalam Optimasi Design Struktur Rangka Sederhana
Pada tugas besar kali ini kita akan mendesign suatu rangka dengan cost yang yang serendah mungkin tetapi dengan kualitas yang optimum. Terdapat beberapa variabel yang diperhatikan diantaranya :
- 1. Harga material
- 2. Jenis material
- 3. Luas Cross Section
- 4. Penampang yang digunakan
Setelah itu kita akan melakukan optimasi dan membentuk kurva efisiensi harga dengan curve fitting menggunakan Metode numerik.
Flowchart Pengerjaan Tugas Besar
1. Mendefinisikan Masalah
2. Menentukan Asumsi Kondisi
Asumsi: - Diasumsikan tidak ada bending karena bersifat truss - Beban terdistribusi pada node - Safety Factor = 2 - Batas displacement 0,001m sebelum terjadi buckling - Variabel bebas Constraint" - Node 1,2,3,4 (lantai dasar) fixed - Beban F1 dan F2 terdistribusi ke node sekitaranya, sehingga: 1. Node 13 & 16 = 1000N 2. Node 14 & 15 = 500N
3. Mengasumsikan Solusi Pada Masalah
Untuk mencapai tujuan hal dapat dilakukan:
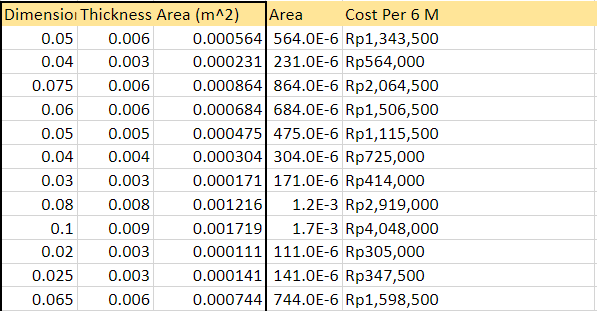
1. Mencari area paling optimum dengan membandingkan dimensi siku untuk menentukan dimensi siku paling optimum (Elastisitas menjadi variabel tetap, Area menjadi variabel bebas)
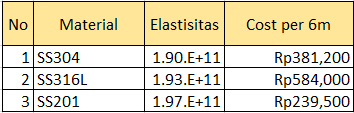
2. Mencari material paling optimum dengan membandingkan performance material pada area yang sama (Area menjadi variabel tetap, Elastisitas menjadi variabel bebas)
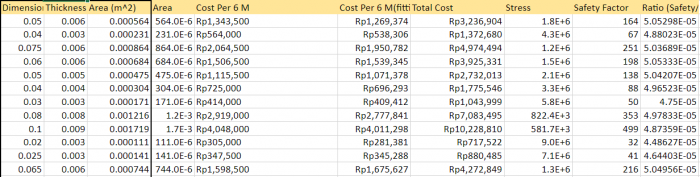
4. Research Data Profil Besi Siku
1. Elasticity Tetap
2. Area Tetap
5. Membuat Model Numerik
1. Menghitung Stress, Displacement, Reaction
model Tugas_Besar_Faridz //define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield= 290.0e+6; //Yield Strength Material(Pa) parameter Real Area= 171.0e-6;//Luas Siku (Dimension=30x30x3mm) parameter Real Elas= 193.0+9; //Elasticity Material (Pa) //define connection parameter Integer C[:,2]=[ 1,5; // (1)
2,6; // (2)
3,7; // (3)
4,8; // (4)
5,6; // (5)
6,7; // (6)
7,8; // (7)
5,8; // (8)
5,9; // (9)
6,10; // (10)
7,11; // (11)
8,12; // (12)
9,10; // (13)
10,11;// (14)
11,12;// (15)
9,12; // (16)
9,13; // (17)
10,14;// (18)
11,15;// (19)
12,16;// (20)
13,14;// (21)
14,15;// (22)
15,16;// (23)
13,16];//(24)
//define coordinates (please put orderly) parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1
0.75,0 ,0,1,1,1; //node 2
0.75,0.6,0,1,1,1; //node 3
0 ,0.6,0,1,1,1; //node 4
0 ,0 ,0.3,0,0,0; //node 5
0.75,0 ,0.3,0,0,0; //node 6
0.75,0.6,0.3,0,0,0; //node 7
0 ,0.6,0.3,0,0,0; //node 8
0 ,0 ,1.05,0,0,0; //node 9
0.75,0 ,1.05,0,0,0; //node 10
0.75,0.6,1.05,0,0,0; //node 11
0 ,0.6,1.05,0,0,0; //node 12
0 ,0 ,1.8,0,0,0; //node 13
0.75,0 ,1.8,0,0,0; //node 14
0.75,0.6,1.8,0,0,0; //node 15
0 ,0.6,1.8,0,0,0]; //node 16
//define external force (please put orderly) parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution Real displacement[N], reaction[N]; Real check[3]; Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3]; protected
parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-15, ers=10e-8;
algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for; //Implementing boundary for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for; //Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F); //Solving reaction reaction:=(G_star*displacement)-F; //Eliminating float error for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for; //Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for; //Calculating stress in each truss for i in 1:Trusses loop for j in 1:3 loop
q1[j]:=P[C[i,1],j]; q2[j]:=P[C[i,2],j]; dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for; //Safety factor for i in 1:Trusses loop
if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if;
end for; end Tugas_Besar_Faridz;
2. Model Curve Fitting
model callcurve
parameter Real [12] X={564.0e-6,231.0e-6,864.0e-6,684.0e-6,475.0e-6,304.0e-6,171.0e-6,1.2e-3,1.7e-3,111.0e-6,141.0e-6,744.0e-6};
parameter Real [12] Y={1343500,564000,2064500,1506500,1115500,725000,414000,2919000,4048000,305000,347500,1598500};
Real [3] Coe;
algorithm
Coe:=Curve_Fitting(X,Y);
end callcurve;
3. Function
function Curve_Fitting
input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1];
protected
Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];
algorithm
for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for;
ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1)); end Curve_Fitting;
4. Optimasi Rangka
model Optimasi_Rangka parameter Real xd[:]={564.0e-6,231.0e-6,864.0e-6,684.0e-6,475.0e-6,304.0e-6,171.0e-6,1.2e-3,1.7e-3,111.0e-6,141.0e-6,744.0e-6}; parameter Real yd[size(xd,1)]={5.05298e-5,4.88023e-5,5.036893e-5,5.05333e-5,5.04207e-5,4.96523e-5,4.75e-5,4.97833e-5,4.87359e-5,4.48627e-5,4.64403e-5,5.04956e-5}; parameter Real xlo=111e-6; parameter Real xhi=1.7e-3; parameter Integer N=10; // maximum iteration parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm xl := xlo; xu := xhi; y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for; end Optimasi_Rangka;
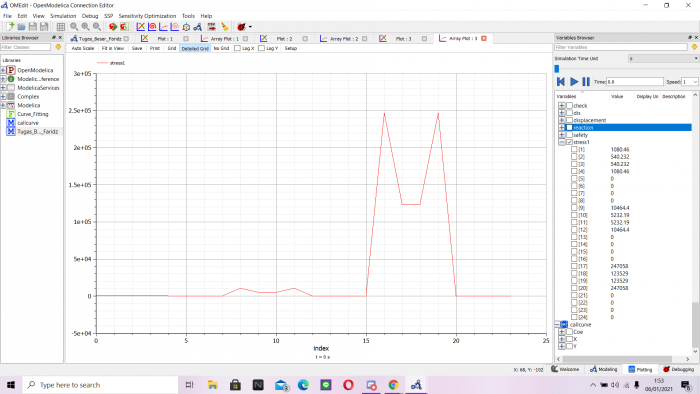
7. Komputasi & Optimasi
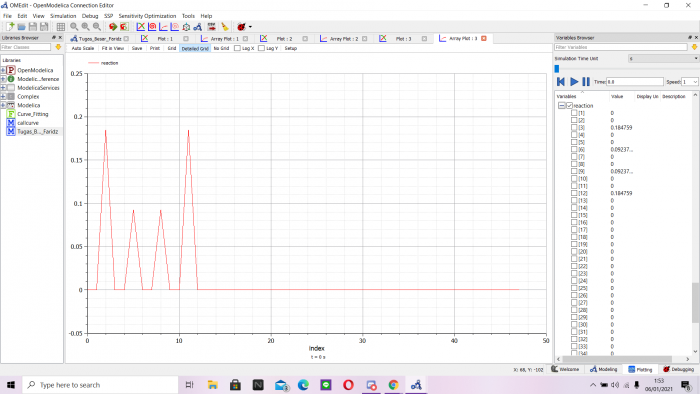
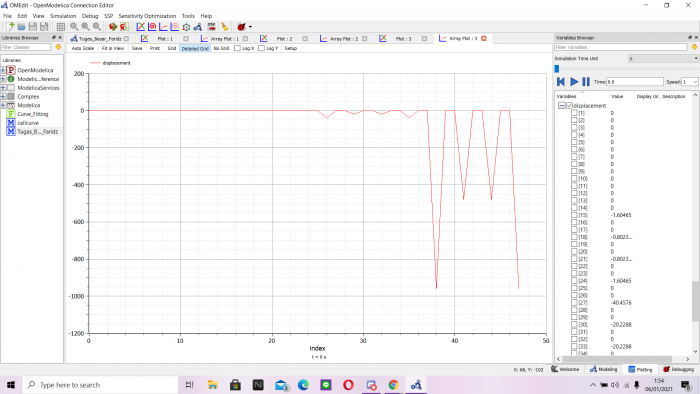
- Nilai Stress
- Nilai Reaction
- Nilai Displacement
Elasticity Tetap
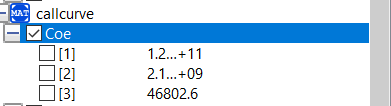
Hasil Curve Fitting
Maka didapatkan data
Kemudian dilakukan Optimasi dengan menggunakan Golden Ratio yang kemudian didapatkan data
Area Tetap