Difference between revisions of "Diyas Prawara Mahdi"

From ccitonlinewiki
Jump to: navigation, search
(→‎Progress Tugas Besar)
Line 803: Line 803:
 
== Progress Tugas Besar ==
 
== Progress Tugas Besar ==
 
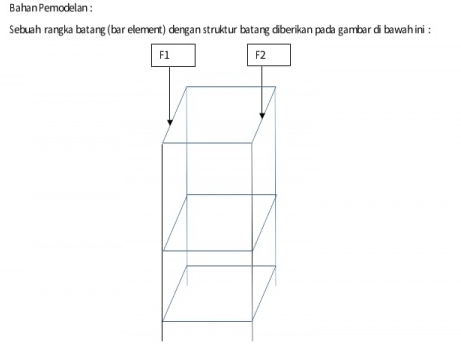
Kami mendapat tugas besar yang diberikan untuk kelas Metode Numerik 02 dan 03 yaitu untuk menghitung dengan menggunakan untuk rangka batang sederhana dengan soal:  
 
Kami mendapat tugas besar yang diberikan untuk kelas Metode Numerik 02 dan 03 yaitu untuk menghitung dengan menggunakan untuk rangka batang sederhana dengan soal:  
−
[[File:SoalTugasBesarDiyas.png|500px|thumb|center]]
+
[[File:SoalTugasBesarDiyas.jpg|500px|thumb|center]]
  
 
dengan spesifikasi:
 
dengan spesifikasi:
  
−
[[File:DataTugasBesarDiyas.png|500px|thumb|center]]
+
[[File:DataTugasBesarDiyas.jpg|500px|thumb|center]]
  
 
Dari soal di ataas, kita mendesign rangka batang dengan harga yang terjangkau dan optimal dengan faktor-faktor (variabel) bebas yaitu harga, material, dan cross section
 
Dari soal di ataas, kita mendesign rangka batang dengan harga yang terjangkau dan optimal dengan faktor-faktor (variabel) bebas yaitu harga, material, dan cross section

Revision as of 15:47, 23 December 2020

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ


736376.jpg


Data Pribadi

Nama: Diyas Prawara Mahdi

NPM: 1906301173

TTL: Jakarta, 5 April 2002

Jurusan: Teknik Mesin

Angkatan: 2019

Email: diyas.prawara@ui.ac.id


Perkenalan Singkat

Nama saya Diyas Prawara Mahdi mahasiswa Teknik Mesin Universitas Indonesia 2019 dan saya adalah salah satu ciptaan terbaik dari Tuhan Yang Maha Esa karena pada prinsipnya Tuhan Yang Maha Esa itu mendesain manusia dengan sebaik-baiknya makhluk.


Saya memilih jurusan teknik mesin dikarenakan saya memiliki ketertarikan di bidang otomotif dan juga powerplant. Alasan lainnya adalah ayah saya yang juga merupakan lulusan teknik mesin ui dan Prof. Indra juga mungkin mengenalnya karena merupakan anak bimbingan Bapak dahulu sehingga menjadi motivasi saya.


Pengalaman Pemograman

Sebelumnya saya belum pernah mempelajari tentang pemograman secara serius namun saya senang membaca-baca buku tentang tutorial menggunakan bahasa pemograman seperti pyton dan lainnya walaupun tidak sampai ke level paham sepenuhnya sehingga saya sudah mendapat gambaran kedepannya akan mempelajari hal apa saja.


Minggu 1 11-11-2020 Metode Numerik

Pada tanggal 11-11-2020, Bapak Dr. Ir. Ahmad Indra Siswantara memberikan penjelasan terlebih dahulu tentang apa itu metode numerik dan apa pentingnya metode numerik. Beliau juga menjelaskan bagaimana cara menggunakan Wiki AIR (Ahmad Indra Research Group). Kemudian kami diajak berdiskusi tentang apa saja manfaat dari mempelajari metode numerik untuk kehidupan dan dunia kerja. Lalu, beliau menjabarkan tentang 4 poin penting penilaian dari beliau yaitu:

1. Matching dengan tujuan belajar: memahami konsep dan prinsip dasar di dalam metnum

2. Dapat menerapkan pemahaman terhadap konsep di dalam permodelan numerik (skill)

3. Mampu menerapkan metnum di dalam persoalan keteknikan (skill)

4. Untuk mencapai poin 1,2,3, harus memiliki hal terpenting, yaitu dengan cara moral value (adab)


Setelah itu, beliau memberikan gambaran penggunaan aplikasi OpenModelica dan mengingatkan kepada kita semua bahwa komputer hanyalah sebuah dummy dan kita (manusia) yang dapat mengatur bagaimana komputer itu bekerja. Sebelum kelas berakhir, beliau memberikan kita dua tugas untuk minggu depan, yaitu:

1. Mempelajari Modelica dari Youtube

2. Membuat video bagaimana kita mempelajari Modelica kemudian diupload ke channel youtube dan cantumkan link nya di wiki air masing masing

Tugas Minggu 1

Dari tugas yang diberikan yaitu mempelajari bagaimana menggunakan aplikasi OpenModelica. OpenModelica adalah aplikasi yang dapat melakukan simulation dan modeling. Sumber ajar yang saya gunakan yaitu melalui platform youtube dan dapat diakses melalui link:

Setelah saya mempelajari bagaimana cara kerja dari OpenModelica, saya lalu mencoba menggunakan aplikasi tersebut sekaligus mencoba mengerjakan perhitungan sederhana yang dapat diakses melalui link:


Minggu 2 18-11-2020 Metode Numerik

Pada minggu kedua, Pak Dai mengawali pertemuan dengan memberikan kata-kata bahwa kita sebagai manusia harus selalu berusaha agar membuat hari ini lebih baik dibanding hari sebelumnya. Kemudian Pak Dai meminta kepada kami untuk memberikan review tentang apa saja manfaat yang dapat diambil dari mempelajari materi aljabar linear. Lalu kita diminta untuk menghubungkan manfaat tersebut dengan metode numerik. Kemudian kami diminta untuk menayangkan hasil pembuatan tugas 1 di OpenModelica kemudian bebas menceritakan atau bertanya tentang hal yang kurang dipahami. Setelah itu, Pak Dai menjelaskan tentang alasan mengajarkan kepada kami aplikasi OpenModelica yaitu karena lisensinya gratis, memiliki fitur yang lengkap, dan mudah digunakan karena aplikasi OpenModelica itu sendiri lebih ke arah bahasa pemodelan sehingga memiliki interface yang lebih mudah digunakan.

Pak Dai kemudian mengajarkan kepada kami salah satu fitur yang ada di OpenModelica, yaitu fitur yang dapan menghubungkan Function dengan Class sehingga dapat memudahkan kami dalam menggunakan OpenModelica. Setelah itu, kami diberikan tugas yaitu membuat sebuah fungsi persamaan aljabar simultan dengan variabel array lalu membuat Class dan memanggil Class ke dalam fungsi tersebut. Hasil pembuatan tugas ini dapat dilihat pada video berikut:


Minggu 3 25-11-2020 Metode Numerik

Pada minggu ketiga, Pak Dai mengajak kita untuk membahas apa saja maanfaat aplikasi metode numerik dalam permasalahan di lingkup teknik. Pak Dai juga menjelaskan software yang dapat digunakan untuk menghitung aplikasi metode numerik di lingkup teknik seperti CFD. Stokastik, dan FEA. Saat kita akan melakukan operasi perhitungan pada masalah teknik, ada urutan agar hasil sesuai, yaitu

1. Melakukan analisis

2. Membuat model matematis

3. Menggunakan software untuk melakukan perhitungan metode numerik berbasis permasalahan teknik

4. Hasil dari perhitungan keluar

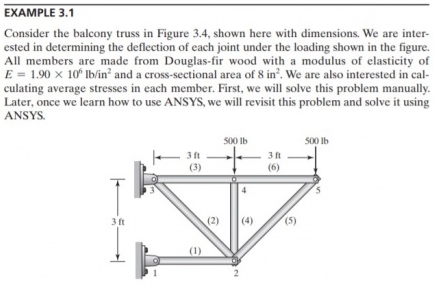
Pada minggu ini, ada dua tugas yang diberikan. Yang pertama adalah tugas sebelum kelas dimulai dan tugas homework. Keduanya menggunakan permasalahan Truss.


TUGAS SEBELUM KELAS

Soal Trusses Latihan Diyas P.jpg

Persamaan 

model Trusses

parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary coundition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];

//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];

//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];

/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);

K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);

G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses;

|}


Soal Trusses Latihan Diyas P 1.jpg
Soal Trusses Latihan Diyas P 2.jpg


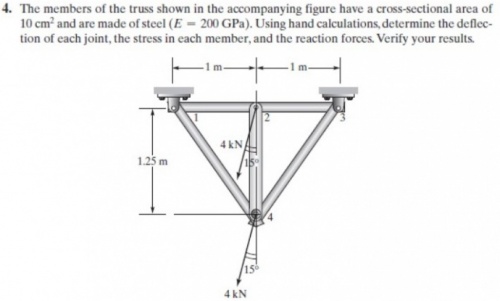
Trusses Problem 2 (Homework)

Persamaan 

class Trusses_PR_Week3

parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary condition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];

//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];

/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);

G:=G1+G2+G3+G4+G5;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses_PR_Week_3;

Fungsi Panggil

Matrice Transformation 

function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;

final constant Real pi=2*Modelica.Math.asin(1.0);

algorithm

Y:=A/180*pi;
    
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;

-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];

for i in 1:4 loop
 for j in 1:4 loop
   if abs(X[i,j]) <= float_error then
     X[i,j] := 0;
   end if;
 end for;
end for;

end Stiffness_Matrices;

Global Element Matrice 

function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];

algorithm

for i in 1:B loop
 for j in 1:B loop
     G[i,j]:=0;
 end for;
end for;

G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];

G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];

G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];

G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];

end Local_Global;

Reaction Matrice Equation 

function Reaction_Trusses
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;

algorithm
X:=A*B-C;

for i in 1:N loop
 if abs(X[i,1]) <= float_error then
   X[i,1] := 0;
 end if;
end for;

for i in 1:N loop
 Sol[i]:=X[i,1];
end for;

end Reaction_Trusses;


Soal Trusses 2 Diyas.jpg
Grafik Displacement
Grafik Reaction Forces






Minggu 4 02-12-2020 Metode Numerik

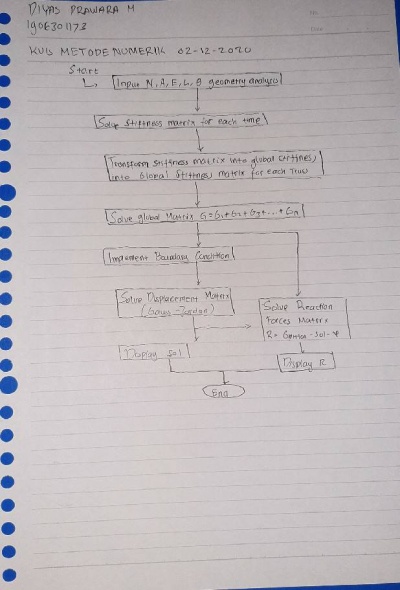
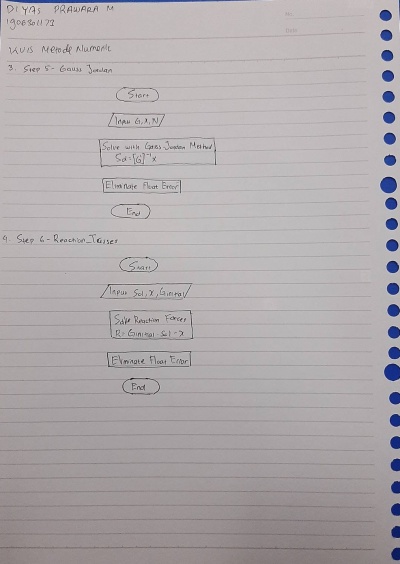
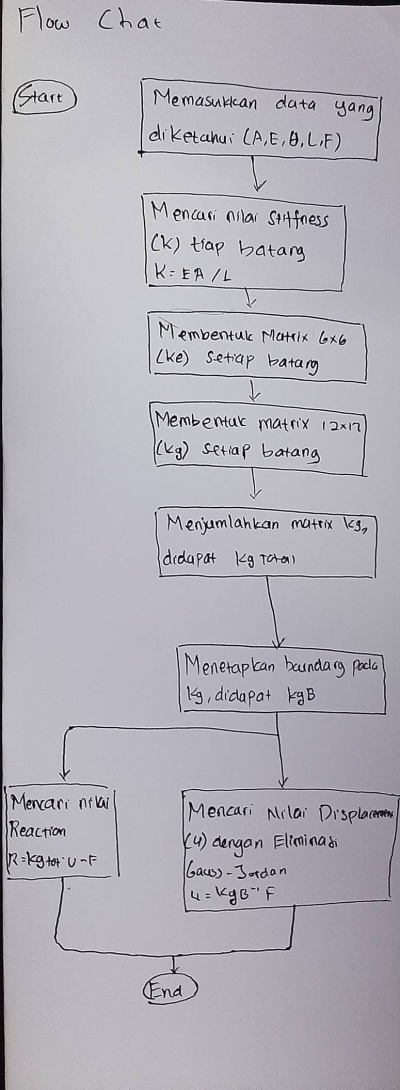
Pada pertemuan hari ini, diawali dengan Pak Dai memberikan motivasi bahwa kita dalam mempelajari metode numerik harus sampai memahami tentang hal-halnya. Setelah itu kami melakukan diskusi tentang bagaimana pengerjaannya dari hasil kerja kami tentang tugas sebelumnya. Kemudian dilanjutkan dengan kami mengerjakan kuis tentang flowchart dengan waktu pengerjaan selama satu jam.

KUIS FLOWCHART DAN CLASS DIAGRAM

Kuis Flow Chart
Kuis Flow Chart
Kuis Flow Chart



Tugas Week 4

Pada minggu ke 4, kami tidak melakukan kegiatan belajar mengajar dikarenakan adanya hari libur sehingga digantikan dengan mengerjakan tugas yang diberikan yaitu membuat flowchart, diagram class, dan coding openmodelica dari soal di bawah.

Tugas Week 4


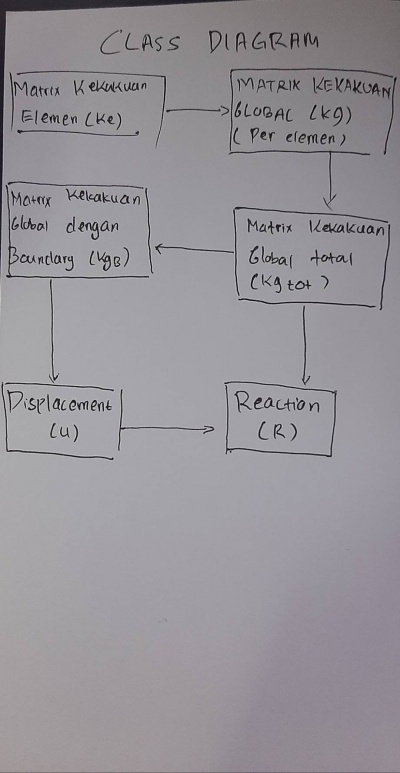
Pertama-tama, saya membuat terlebih dahulu Class Diagram dan Flowchart

Class Diagram
Flow Chart


Kemudian saya melanjutkan dengan membuat FBD

FBD

function StiffnessMatrixElement 

 input Real [:,9] inisiasi_mat;
 output Real [size(inisiasi_mat,1),6,6] Ke_mat;

 protected
   Real cos_x;
   Real cos_y;
   Real cos_z;
   Real [6] StiffTrig;
   Real [6,6] StiffTrans;
   Real [size(inisiasi_mat,1)] k_vec;

algorithm 

 k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)};

 // Finding stiffness matrix of each element member
 for i in 1:size(inisiasi_mat,1) loop

 // Clearing the matrices
 StiffTrig := zeros(6);
 StiffTrans := zeros(6,6);
 
 // Converting degrees to radians
 cos_x := inisiasi_mat[i,4];
 cos_y := inisiasi_mat[i,5];
 cos_z := inisiasi_mat[i,6];

 // {cos^2, sin^2, sincos}
 StiffTrig := {(cos_x)^2,
               (cos_y)^2,
               (cos_z)^2,
               (cos_x*cos_y),
               (cos_x*cos_z),
               (cos_y*cos_z)};
 
 // Construct stiffness transformation matrix
 StiffTrans := [  StiffTrig[1],    StiffTrig[4],    StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
                  StiffTrig[4],    StiffTrig[2],    StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
                  StiffTrig[5],    StiffTrig[6],    StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
               -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5],    StiffTrig[1],    StiffTrig[4],    StiffTrig[5];
               -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6],    StiffTrig[4],    StiffTrig[2],    StiffTrig[6];
               -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3],    StiffTrig[5],    StiffTrig[6],    StiffTrig[3]];
               
 // Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
 for m in 1:6 loop
   for n in 1:6 loop
     Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
   end for;
 end for;

end for; end StiffnessMatrixElement;




function StiffnessMatrixGlobal 

 input Integer [:,2] n;
 input Integer x;
 input Integer y;
 input Real [y,6,6] Ke_mat; 
 output Real [y,x,x] Kg_mat;

algorithm 

 for i in 1:y loop
   for a in 1:x loop
     for b in 1:x loop
       Kg_mat[i,a,b]:=0;
     end for;
   end for;
  end for;

 for i in 1:y loop
   Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
   Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
   Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
   Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
   Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
   Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
   Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
   Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
   Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];

   Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6];
   Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5];
   Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4];
   Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6];
   Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5];
   Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4];
   Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6];
   Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5];
   Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];

   Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3];
   Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2];
   Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1];
   Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3];
   Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2];
   Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1];
   Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3];
   Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2];
   Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];

   Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6];
   Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5];
   Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4];
   Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6];
   Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5];
   Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4];
   Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6];
   Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5];
   Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4];
 end for;

end StiffnessMatrixGlobal;



function SumStiffnessMatrixGlobal 

 input Integer x;
 input Integer y;
 input Real [y,x,x] Kg_mat;
 output Real [x,x] KgTot_mat;

algorithm 

  for a in 1:x loop
   for b in 1:x loop
     KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
    end for;
   end for;

end SumStiffnessMatrixGlobal;



function BoundaryStiffnessMatrixGlobal 

 input Integer x;
 input Integer z;
 input Real [x,x] KgTot_met;
 input Integer[z] Boundary_met;
 output Real [x,x] KgB_met;

algorithm 

 for a in 1:x loop
   for b in 1:x loop
    KgB_met[a,b] := KgTot_met [a,b];
   end for;
  end for; 
 
 for i in 1:x loop
  for a in 1:z loop
   for b in 0:2 loop
     KgB_met[3*(Boundary_met[a])-b,i]:=0;
   end for;
  end for;
 end for;

 for a in 1:z loop
   for b in 0:2 loop
     KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1;
   end for;
 end for;

end BoundaryStiffnessMatrixGlobal;



function GaussJordan 

 input Integer x;
 input Real [x,x] KgB_met;
 input Real [x] load_met;
 output Real [x] U_met;
 
 protected
 Real float_error = 10e-10;

algorithm 

 U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);

 for i in 1:x loop
   if abs(U_met[i]) <= float_error then
    U_met[i] := 0;
   end if;
 end for;

end GaussJordan;



function ReactionForce 

 input Integer x;
 input Real [x,x] KgTot_met;
 input Real [x] U_met;
 input Real [x] load_met;
 output Real [x] R_met;

algorithm 

 R_met := (KgTot_met*U_met)-load_met;

end ReactionForce;



class TugasWeek4 

 parameter Real [:,9] inisiasi = [1, 1, 2, -0.8,    0, -0.6, 15e-4, 70e9, 2.5;
                                  2, 1, 3, -0.8, -0.6,    0, 15e-4, 70e9, 2.5;
                                  3, 1, 4, -0.8,    0,  0.6, 15e-4, 70e9, 2.5];
                                  
 parameter Integer [:,2] node = [1, 2;
                                 1, 3;
                                 1, 4];
                                 
 parameter Integer y = size(node,1);
 
 parameter Integer x = 3*(size(node_load,1));
 
 parameter Integer z = size(Boundary,1);
 
 parameter Integer [:] Boundary = {2,3,4};
                              
 parameter Real [:,4] node_load = [1, 0, -5000, 0;
                                   2, 0,     0, 0;
                                   3, 0,     0, 0;
                                   4, 0,     0, 0];
                                   
 parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
                                  
 Real [y] k;

 Real [y,6,6] Ke;
 
 Real [y,x,x] Kg;
 
 Real [x,x] KgTot;
 
 Real [x,x] KgB;
 
 Real [x] U;
 
 Real [x] R;

equation 

k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};

Ke = StiffnessMatrixElement(inisiasi);

Kg = StiffnessMatrixGlobal(node, x, y, Ke);

KgTot = SumStiffnessMatrixGlobal(x, y, Kg);

KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);

U = GaussJordan(x, KgB, load);

R = ReactionForce(x, KgTot, U, load);

end TugasWeek4;



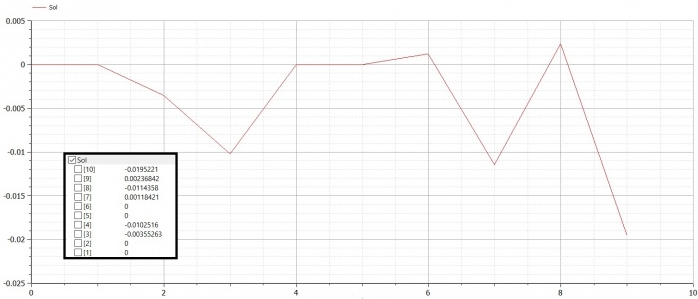
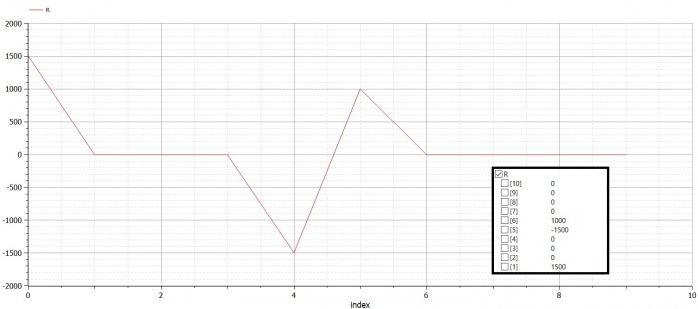
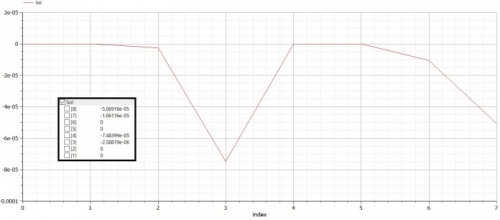
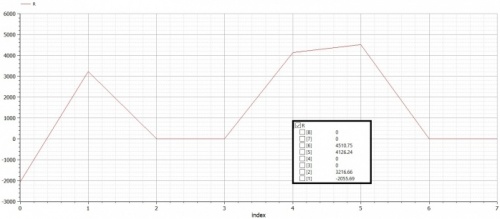
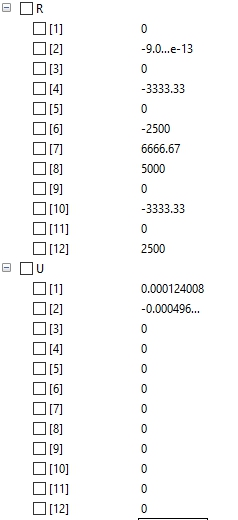
Setelah disimulate, kita mendapatkan nilai displacement (U) dan R

1607500518690.jpg

Video penjelasan dapat dilihat melalui link Video Penjelasan Tugas Week 4 atau dari video di bawah ini


Minggu 5 14-12-2020

Pertemuan week 5 dilakukan pada hari Senin, 14-12-2020 dikarenakan pada tanggal 11-12-2020 merupakan hari libur nasional dalam rangka pilkada

Minggu 6 16-12-2020

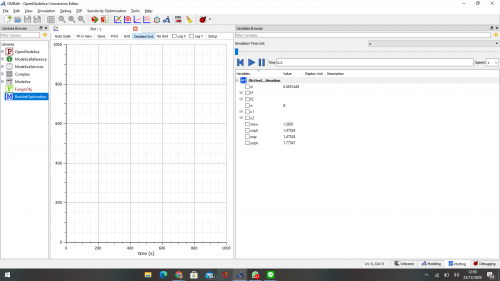
Pada pertemuan minggu ini, kami terlebih dahulu menonton video yang diberikan oleh Bu Chandra tentang Kasus Optimasi menggunakan metode bracket.. Setelah menonton video tersebut, saya mencoba untuk membuat perhitungan optimasi tesebut dengan referensi dari video Bu Chandra sehingga saya mendapatkan hasil sebagai berikut:

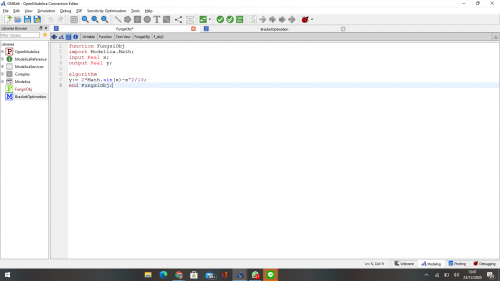
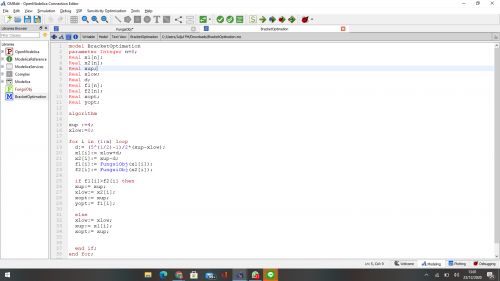
untuk fungsi:

FungsiKasusOptimasiDiyas.png

untuk bracket:

BracketKasusOptimasiDiyas.png


sehingga dari fungsi dan model yang sudah saya buat, saya mendapatkan hasil yaitu:

HasilJawabanKasusOptimasiDiyas.png

Aplikasi Metode Numerik Dalam Kasus Optimasi


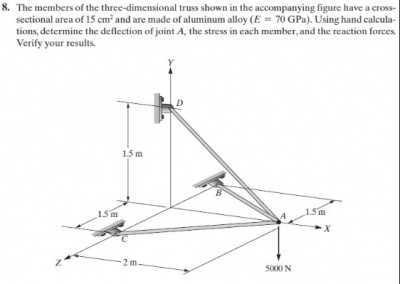
Progress Tugas Besar

Kami mendapat tugas besar yang diberikan untuk kelas Metode Numerik 02 dan 03 yaitu untuk menghitung dengan menggunakan untuk rangka batang sederhana dengan soal:

SoalTugasBesarDiyas.jpg

dengan spesifikasi:

DataTugasBesarDiyas.jpg

Dari soal di ataas, kita mendesign rangka batang dengan harga yang terjangkau dan optimal dengan faktor-faktor (variabel) bebas yaitu harga, material, dan cross section

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Diyas_Prawara_Mahdi&oldid=50593"