Difference between revisions of "Norman Febrianto"
| Line 351: | Line 351: | ||
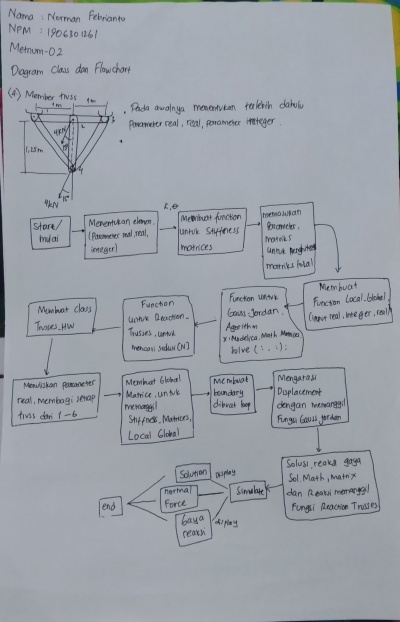
Pembuatan diagram class dan flowchart dari soal adalah sebagai berikut : | Pembuatan diagram class dan flowchart dari soal adalah sebagai berikut : | ||
[[File:Dclassno8.jpg|400px|center]] | [[File:Dclassno8.jpg|400px|center]] | ||
| + | |||
[[File:Fchartno8.jpg|400px|center]] | [[File:Fchartno8.jpg|400px|center]] | ||
| + | |||
pertama kita bahas dengan mencari diketahui, dan menuliskan parameter yang ada dengan menghitung | pertama kita bahas dengan mencari diketahui, dan menuliskan parameter yang ada dengan menghitung | ||
[[File:Dikno8.jpg|500px|center]] | [[File:Dikno8.jpg|500px|center]] | ||
| + | |||
kemudian menuliskan function yang terlibat dalam pengerjaan soal, pertama adalah function element matrices | kemudian menuliskan function yang terlibat dalam pengerjaan soal, pertama adalah function element matrices | ||
[[StiffnessMatrixElement.png|500px|center]] | [[StiffnessMatrixElement.png|500px|center]] | ||
| + | |||
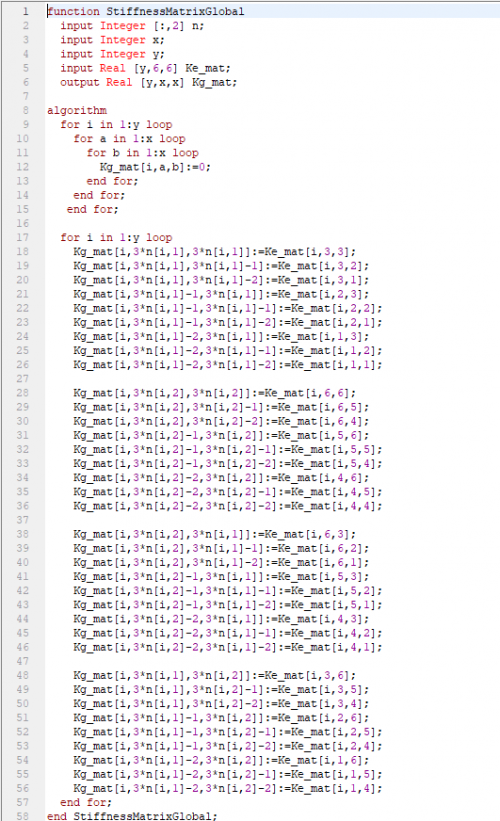
Kemudian matriks untuk stiffness global | Kemudian matriks untuk stiffness global | ||
[[File:StiffnessMatrixGlobal.png|500px|center]] | [[File:StiffnessMatrixGlobal.png|500px|center]] | ||
| + | |||
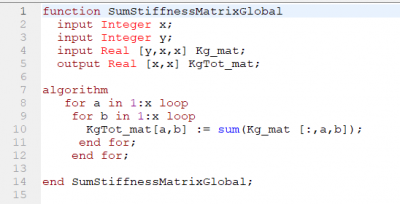
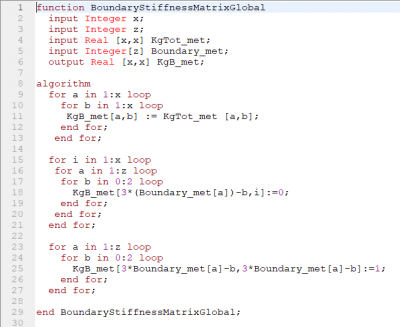
Setelah itu dapat kita jumlahkan matriks global, dan menentukan boundary dari matriks | Setelah itu dapat kita jumlahkan matriks global, dan menentukan boundary dari matriks | ||
[[File:SumStiffnessMatrixGlobal.png|400px|left]] | [[File:SumStiffnessMatrixGlobal.png|400px|left]] | ||
[[File:BoundaryStiffnessMatrixGlobal.png|400px|right]] | [[File:BoundaryStiffnessMatrixGlobal.png|400px|right]] | ||
| + | |||
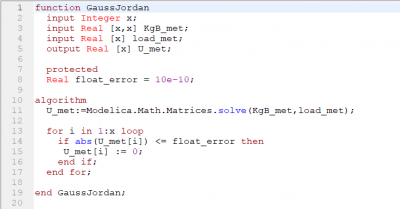
Kemudian kita bisa memanggil fungsi Gaussjordan, dan menentukan Reaksi dengan fungsi reaction | Kemudian kita bisa memanggil fungsi Gaussjordan, dan menentukan Reaksi dengan fungsi reaction | ||
[[File:GaussJordan.png|400px|left]] | [[File:GaussJordan.png|400px|left]] | ||
[[File:File:ReacN.jpg|400px|right]] | [[File:File:ReacN.jpg|400px|right]] | ||
| + | |||
setelah itu akan didapatkan hasil U(displacement) dan R(Reaction) | setelah itu akan didapatkan hasil U(displacement) dan R(Reaction) | ||
[[File:U&R.png|500px|center]] | [[File:U&R.png|500px|center]] | ||
Berikut link video yang saya buat untuk menjelaskan mengenai proses coding atau pengerjaan soal no.8 | Berikut link video yang saya buat untuk menjelaskan mengenai proses coding atau pengerjaan soal no.8 | ||
Revision as of 15:57, 9 December 2020
Contents
Data Diri
- Nama : Norman Febrianto
- NPM : 190630161
- Jurusan : Teknik Mesin
- Angkatan: 2019
Perkenalan Singkat
Nama saya Norman Febrianto dari jurusan Mesin Universitas Indonesia. Saya memilih jurusan mesin karena ingin lebih mengetahui dunia permesinan dan prospek kerja jurusan mesin yang cukup luas.
Metode Numerik
Metode numerik merupapakan teknik dalam penyelesaian permsalahan yang diformulasikan secara matematis dengan menggunakan operasi hitungan (aritmatik) yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan matematis tidak dapat diselesaikan menggunakan metode analitik. Materi yang telah disampaikan dalam mata kuliah Metode Numerik diantaranya :
Pseudocode
- Sistem Persamaan
- Turunan Numerik
- Metode Newton Rhapson, Secant, dan Bisection
- Regresi Linear
- Interpolasi
Metode Numerik Minggu ke-1
Dalam belajar metode numerik, terdapat hal-hal yang harus diperhatikan diantaranya :
- paham melalui konsep-konsep yang telah diberikan, beberapa materi dalam metode numerik : memahami persamaan, istilah algoritma, kurva, regresi, differensial, parsial
- Dapat menerapkan pemahaman terhadap konsep dalam permodelan numerik, bisa menyelesaikan masalah melalui perhitungan numerik
- menerapkan metode dalam permasalahan keteknikan
- dapat mencapai poin 1,2,3 juga dengan moral value yaitu adab
Tugas Minggu ke-1
Mempelajari dan membuat video tutorial menggunakan open modelica, saya sudah membuat video tutorial yang tidak begitu sulit dengan open modelica mengenai interpolasi. berikut contoh soal yang saya coba menyelesaikan dengan openmodelica.
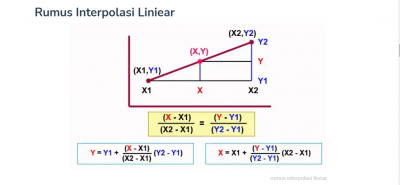
Kita dapat menyelesaikan persoalan berikut dengan menggunakan rumus umum dari interpolasi.
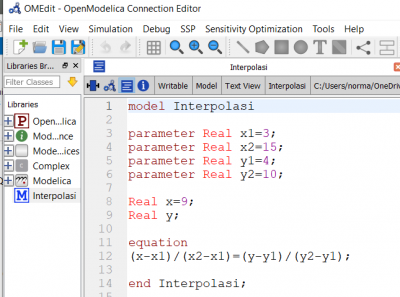
Kemudian kita dapat memasukan variabel-variabel yang diketahui, untuk parameter real berdasarkan soal diantaranya x1, x2, y1, y2. Variabel yang akan kita cari adalah y dan dapat kita tuliskan "Real y". Kita juga bisa menuliskan Real x meskipun x sudah diketahui pada open modelica.
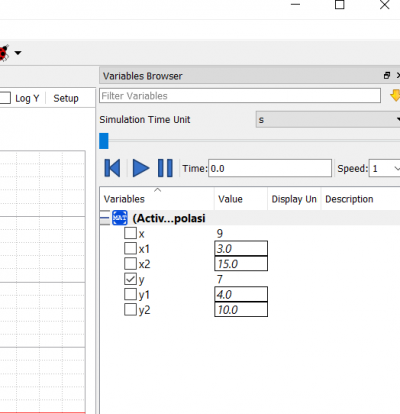
Setelah di check, jika tidak terdapat masalah kita save terlebih dahulu dan dapat dilakukan stimulate untuk proses pada openmodelica. Hasil dari Real y yang dicari didapatkan pada box sebelah kanan.
berikut link video saya pada saat mengerjakan interpolasi di atas
saya mempelajari open modelica dari link video berikut : https://www.youtube.com/watch?v=GhtBMIlO70w
Metode Numerik Minggu ke-2
Openmodelica lebih ke bahasa permodelan, bukan hanya bahasa coding seperti pyhton. Namun dalam perhitungan menggunakan code yang dalam bahasa C++, parameter real tidak perlu dicompile ulang cukup di simulate ulang saja. kelebihan openmodelica diantaranya sebagai berikut :
- 1. menggunakan bahasa permodelan yang cocok untuk engineer
- 2. segi perhitungan lumayan cepat
- 3. pengguna aplikasi openmodelica cukup banyak penggunanya, dan termasuk open teknologi (free). Karena seperti mathlab harus membeli atau ada legalisasi
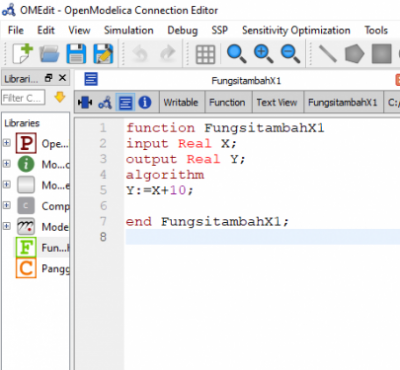
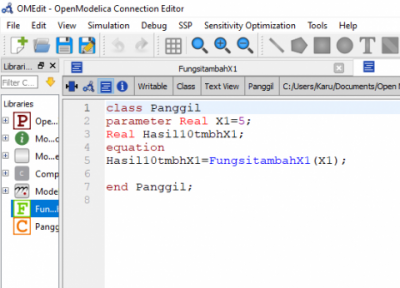
Pada minggu ini, belajar cara untuk memanggil suatu fungsi untuk class tertentu. Jadi pada langkahnya pada awal new, memilih pada option Function untuk membuat fungsi yang nantinya akan digunakan untuk membantu perhitungan. Function dinamakan "Fungsi Tambah X1"dengan X sebagai input, Y sebagai output, dan fungsi yang dibuat adalah Y=10+x. Dibuat dalam Open Modelica sebagai berikut:
Selanjutnya membuat new (baru) untuk memilih option class dinamakan "Panggil" yang digunakan untuk "memanggil" fungsi tambah X1 tersebut. Pada class ini, kita dapat mengubah nilai input X1 sesuai dengan kebutuhan.
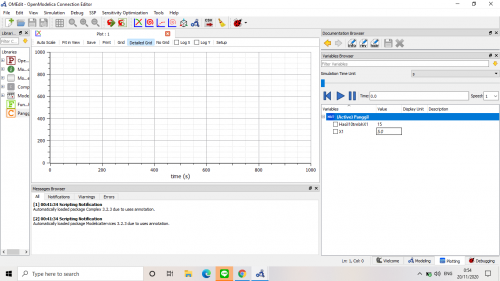
Setelah itu, pada class untuk memakai function yang telah dibuat kita panggil pada "equation". Jadi Function digunakan untuk membantu perhitungan pada class ini. nilai output Y merupakan nilai yang dicari sesuai dengan nilai input X1 yang dimasukan. Sebagai contoh, dimasukkan nilai X1 sebesar 5 maka sesuai fungsi Y=10+X, akan didapatkan nilai Hasil+X1=10+X1=10+5=15.
Nilai outpu Y terlihat pada box di sebelah kanan. Nilai X1 dapat dirubah sesuai dengan kebutuhan dan dapat dilakukan re-simulate untuk mendapatkan nilai outputnya.
Tugas Minggu ke-2
Pengaplikasikan penggunaan Function dan Class pada Openmodelica. membuat sebuah fungsi berupa persamaan aljabar simultan dengan variabel array kemudian membuat class untuk memanggil fungsi tersebut. Persamaan aljabar simultan adalah sebuah persoalan matematika yang kompleks sehingga penyelesaian perlu dengan menggunakan tools, agar dapat dibuat lebih sederhana. Metode yang dapat digunakan untuk menyelesaikan persamaan aljabar simultan adalah metode Gauss, Gauss-Jordan, Crammer, dan Gauss-Seidel. Variabel array adalah sebuah variabel yang di dalamnya terdapat banyak data. Contoh, jika kita memiliki data X1,X2,...,X10 menggunakan variabel array cukup dituliskan X[10] Untuk mencoba menggunakan Function and Class, saya mencoba menjawab soal matriks 4x4 dari contoh soal yang saya browsing di internet.
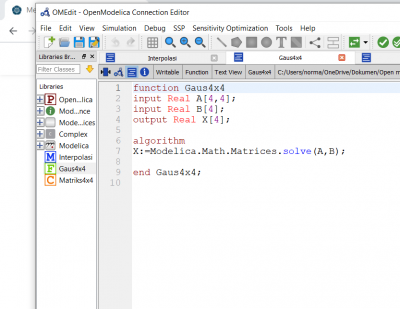
Kemudian kita dapat membuat fungsi Gauss untuk matriks 4x4 terlebih dahulu. Pada function saya memakai fungsi "solve" eliminasi gauss dari openmodelica yang dapat digunakan untuk menyelesaikan persamaan matriks
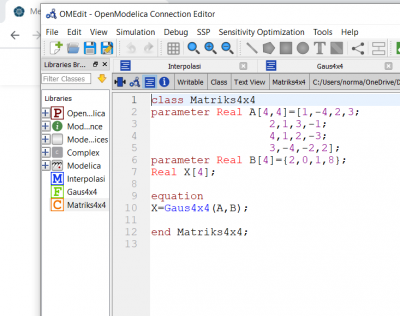
Langkah selanjutnya membuat class yang berisikan matriks dari soal, dan untuk menggunakan function yang telah dibuat sebelumnya.
Setelah itu dilakukan stimulate, sehingga didapatkan hasil matriks berikut
berikut video saya untuk penerapan tugas ke-2 mengenai Function & classMetode Numerik Minggu ke-3
membuat fungsi di dalam modelica untuk menyelesaikan persamaan aljabar pada buku (9.12) dengan metode Gauss, namun bisa juga menggunakan metode lain seperti Gauss-Jordan. penyelesaian yang hasilnya berupa himpunan disebut array. menggunakan array karena nilai uji akan berubah perr-iterasi, iterasi 1 nilai A, ke-2 B, sehingga hasilnya berupa himpunan penyelesaian dan berupa grafik. [N] merupakan jumlah dari data, dapat juga menjadi 3 dimensi dengan menambahkan variabel lain [O], [P], dan lainnya. Beberapa metode yang dapat digunakan yaitu CFD, Stokastik, dan FEA. Dalam menyelesaikan masalah teknik, angkah yang harus dilakukan adalah melakukan analisis, membuat model matematis, menggunakan metode numerik untuk penyelesain (menggunakan computer), dan didapatkan solusi dari permasalahan. Salah satu permasalahan teknik yang dijadikan contoh adalah mengenai Truss.
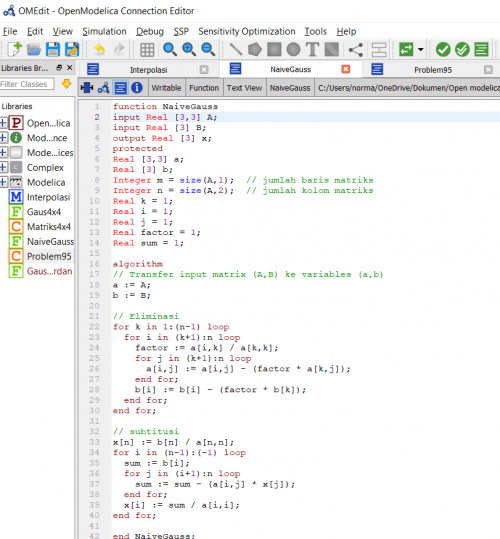
Pada kelas kali ini, sebelumnya diriview kembali mengenai aljabar simultan untuk menyelesaikan persamaan linier dengan matriks. Pengaplikasian dalam Open Modelica, kita akan membuat code untuk menyelesaikan persamaan 9.12 pada buku Chapra yaitu mengenai eliminasi Naïve Gauss. Pseudocode untuk eliminasi Naïve Gauss diberikan pada Fig.9.4:
pada open modelica dapat dituliskan dengan menggunakan Function, dinamakan "NaiveGauss"
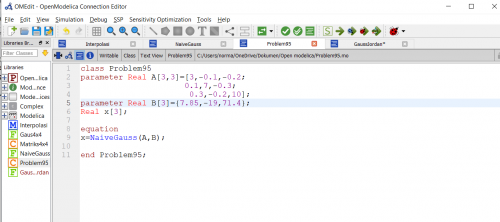
Kemudian dapat dipanggil function sebelumnya kedalam class
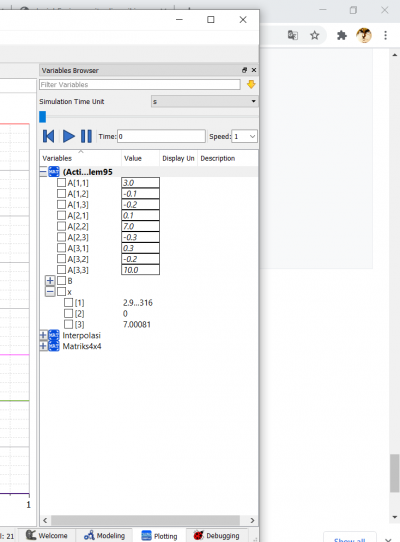
Setelah itu dapat kita stimulate untuk di dapatkan hasilnya
Tugas Minggu ke-3
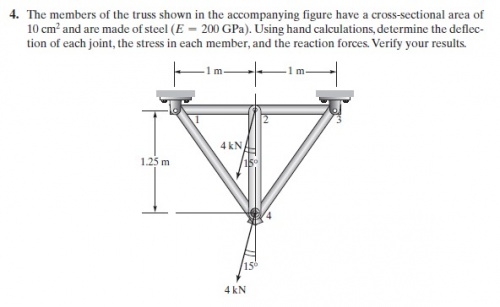
Mencoba mengerjakan soal permasalahan teknik yaitu Truss, dengan menggunakan openmodelica. Berikut soal yang harus dikerjakan
Berikut merupakan Program yang dibuat pada modelica untuk penyelesaian
*class TrussesHW
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
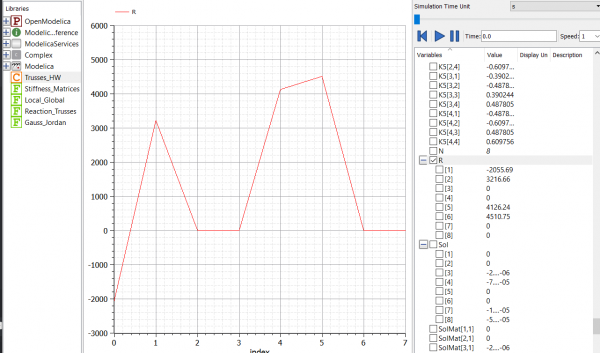
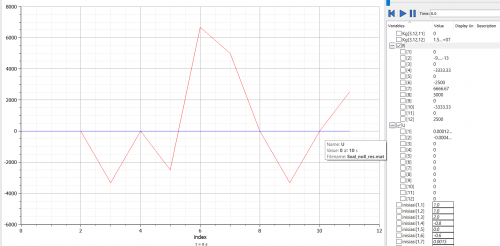
end Trusses_HW;Grafik Reaction Process
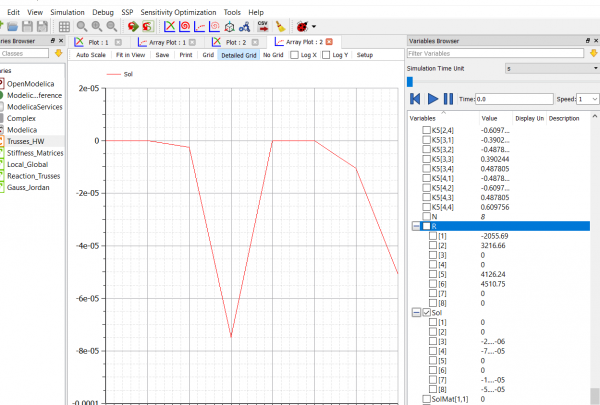
Grafik Diplacement
Transformasi Matriks
function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;Global Element Matrice
function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
Reaction Matrice Equation
function Reaction_Trusses
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;
algorithm
X:=A*B-C;
for i in 1:N loop
if abs(X[i,1]) <= float_error then
X[i,1] := 0;
end if;
end for;
for i in 1:N loop
Sol[i]:=X[i,1];
end for;
end Reaction_Trusses;Gauss Jordan
function Gauss_Jordan
input Integer N;
input Real A[N,N];
input Real B[N];
output Real X[N];
Real float_error = 10e-10;
algorithm
X:=Modelica.Math.Matrices.solve(A,B);
for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end Gauss_Jordan;Metode Numerik Minggu ke-4
Quiz Flowchart dan class diagram
pada minggu ke-4 memahami mengenai flowchart berdasarkan coding yang dibuat josiah, berikut jawaban dari saya
Tugas Minggu ke-4
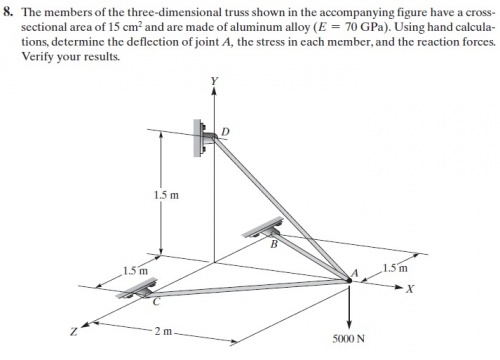
Pada minggu ke empat, kami perlu mengerjakan soal no.8 mengenai truss 3 Dimensi dengan menggunakan open modelica, berikut soal yang harus dikerjakan dan dipahami.
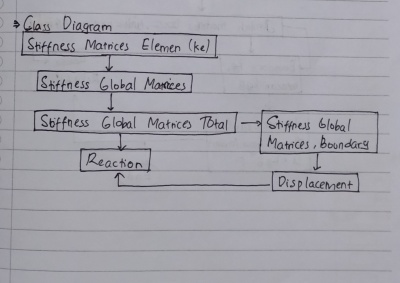
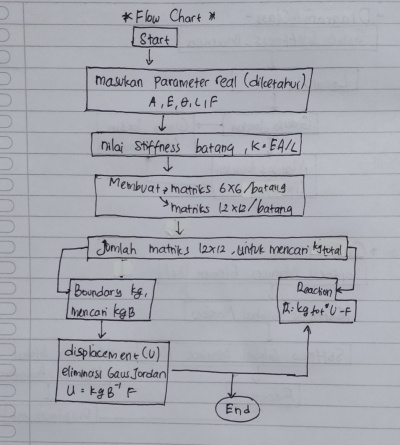
Pembuatan diagram class dan flowchart dari soal adalah sebagai berikut :
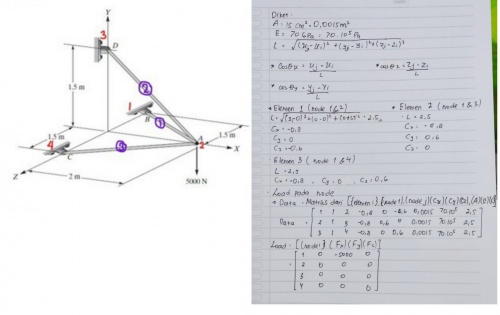
pertama kita bahas dengan mencari diketahui, dan menuliskan parameter yang ada dengan menghitung
kemudian menuliskan function yang terlibat dalam pengerjaan soal, pertama adalah function element matrices 500px|center
Kemudian matriks untuk stiffness global
Setelah itu dapat kita jumlahkan matriks global, dan menentukan boundary dari matriks
Kemudian kita bisa memanggil fungsi Gaussjordan, dan menentukan Reaksi dengan fungsi reaction
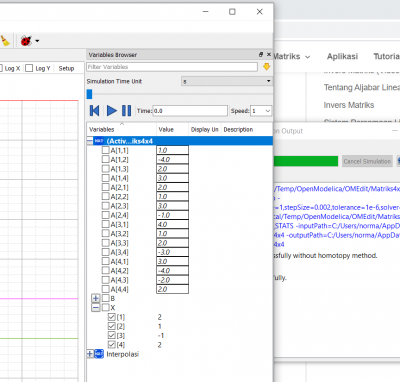
setelah itu akan didapatkan hasil U(displacement) dan R(Reaction)
Berikut link video yang saya buat untuk menjelaskan mengenai proses coding atau pengerjaan soal no.8