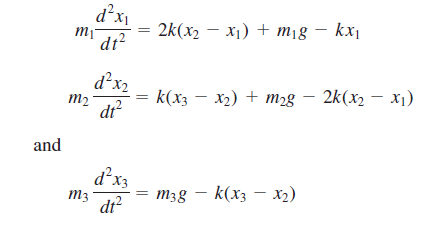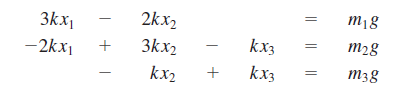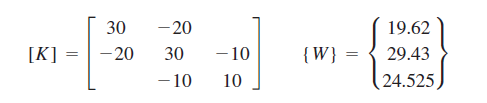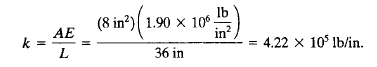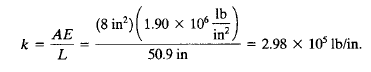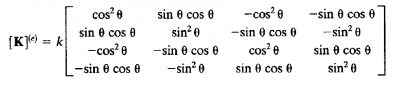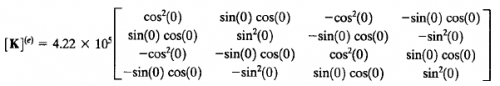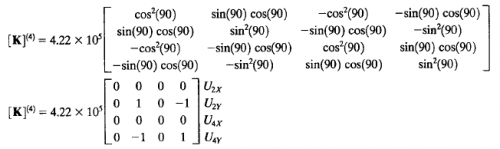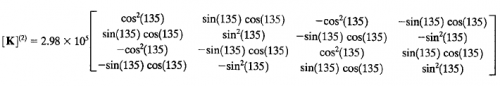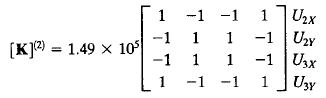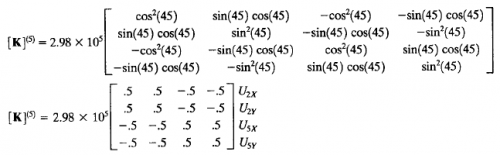Difference between revisions of "Metnum03-Wildan Firdaus"
| Line 369: | Line 369: | ||
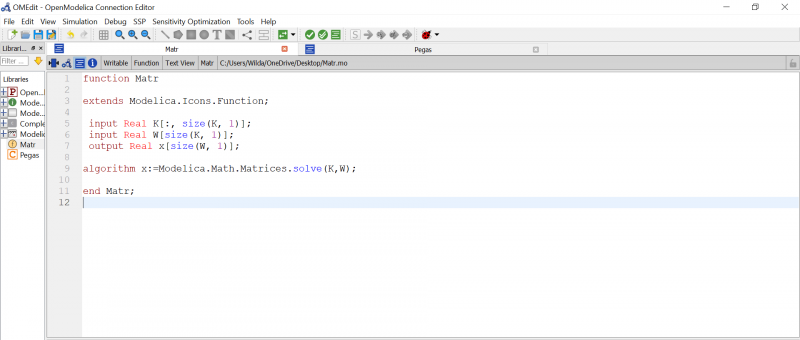
[[File:Reaksi 2D.png|500px|thumb|center]] | [[File:Reaksi 2D.png|500px|thumb|center]] | ||
| + | |||
| + | |||
| + | |||
| + | NO.8 | ||
| + | |||
| + | Pertama yang harus dilakukan adalah membuat tabel, berisi nama element, node, dan sudut setiap batang terhadap sumbu X positif. Setelah itu menentukan nilai kekakuan pada setiap batang. | ||
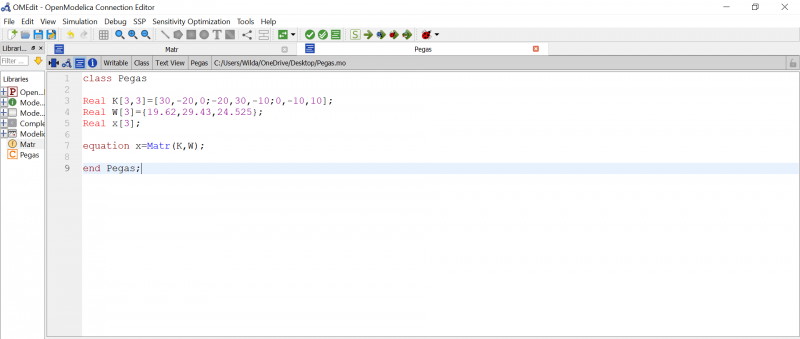
[[File:3D.jpeg|500px|thumb|center]] | [[File:3D.jpeg|500px|thumb|center]] | ||
| + | |||
| + | |||
| + | Setelah itu kita membuat K lokal untuk setiap batang menggunakan fungsi dan class pada OpenModelica | ||
| + | |||
[[File:K3D1.png|500px|thumb|center]] | [[File:K3D1.png|500px|thumb|center]] | ||
| Line 378: | Line 388: | ||
[[File:K Lokal 3D.png|500px|thumb|center]] | [[File:K Lokal 3D.png|500px|thumb|center]] | ||
| + | |||
| + | |||
| + | Setelah didapatkan nilai K lokal, kita konversi menjadi K global pada setiap batang. Kemudian nilai K pada setiap batang ini dijumlahkan menjadi K global total. Disini saya menggunakan perhitungan manual menggunakan bantuan excel, sehingga menghasilkan sebagai berikut. | ||
| + | |||
| + | |||
| + | [[File:Exc3.png|500px|thumb|center]] | ||
| + | |||
| + | |||
| + | Setelah dimasukan kondisi batas UxB, UyB, UzB, UxC, UyC, UzC, UxD, UyD, UzD= 0. Maka matrixnya akan menjadi berukuran 3 x 3 | ||
| + | |||
| + | |||
| + | [[File:Exc4.png|500px|thumb|center]] | ||
| + | |||
| + | |||
| + | Sehingga untuk U dan R nya menjadi seperti berikut : | ||
[[File:Gauss_Jordan3D.png|500px|thumb|center]] | [[File:Gauss_Jordan3D.png|500px|thumb|center]] | ||
Revision as of 12:15, 7 December 2020
Assalamualaikum Warahmatullahi Wabarakatuh
Contents
- 1 BIODATA DIRI
- 2 Pertemuan Metode Numerik 1 : 09 November 2020
- 3 PR 1 Belajar OpenModelica
- 4 Pertemuan Metode Numerik 2 : 16 November 2020
- 5 PR 2 Aljabar Simultan dengan OpenModelica
- 6 Pertemuan Metode Numerik 3 : 23 November 2020
- 7 PR 3 Menghitung Dispalcement dan Gaya Reaksi pada Balconi Truss dengan OpenModelica
- 8 Pertemuan Metode Numerik 4 : 30 November 2020 Quiz 1
BIODATA DIRI
Nama : Wildan Firdaus
NPM : 1906435574
Fakultas/ Jurusan : Teknik/ Teknik Mesin
Kelas Metode Numerik 03
Pertemuan Metode Numerik 1 : 09 November 2020
Metode numerik merupakan teknik penyelesaian permsalahan matematis dengan menggunakan operasi hitungan yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan matematis tidak dapat diselesaikan menggunakan metode analitik. Jikapun terdapat penyelesaiannya secara analitik, proses penyelesaiaannya sering kali cukup rumit dan memakan banyak waktu sehingga tidak efisien. Sebelum UTS kami mempelajari berbagai materi pokok mengenai metode numerik yaitu mencari akar akar persamaan non linear, turunan numerik, regresi dan interpolasi.
1. Mencari akar akar persamaan non linear
Pada materi ini saya mempelajari cara cara menghitung akar persamaan non liner secara numerik dengan 2 metode yaitu close methods dan open methods. Closed Methods merupakan metode pencarian akar-akar dengan menggunakan batas atas dan batas bawah untuk mencari akar dan mengukur persentasi error yang didapat untuk mendapat tingkat akurasi dari iterasi. Metode yang saya pelajari ada 3 yaitu Graphical Methods, Bisection Methods, dan False-Position Methods. Sedangkan Open Methods merupakan metode pencarian yang hanya menggunakan 1 titik untuk menemukan akar-akar. Metode ini dapat menggunakan turunan suatu fungsi untuk menentukan titik pengujian baru yang semakin dekat dengan nilai akar-akar yang diinginakn. Metode yang saya pelajari ada 3 yaitu Fixed-Point Iteration, Newton-Rapshon, dan Secant Method
2. Turunan numerik
Turunan Numerik adalah menentukan nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdapat 3 pendekatan dalam menghitung turunan numerik:
3. Regresi
Regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variable terikat Y dan satu atau lebih variable bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Hubungan di antara variable-variabel tersebut disebut sebagai model regresi linear.
4. Interpolasi
Interpolasi adalah metode menghasilkan titik-titik data baru dalam suatu jangkauan dari beberapa data-data yang diketahui.
PR 1 Belajar OpenModelica
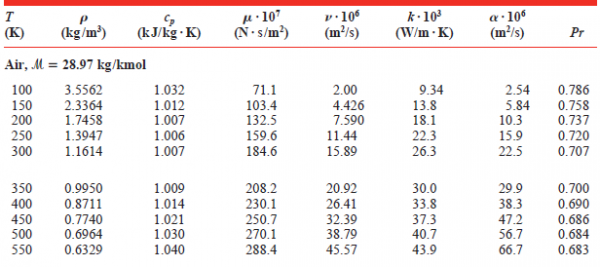
Pada tugas minggu ini saya menggunakan materi interpolasi dalam penerapan metode numerik menggunakan aplikasi open modelica. Saya menggunakan interpolasi untuk mencari data properties udara berupa massa jenis, kapasitas panas, viskositas dinamik, viskositas kinematik, konduktivitas termal, difusivitas termal dan prandtl number untuk udara dengan temperatur 100 derajat celcius atau setara dengan 373 derajat kelvin. Data data yang dikaetahu adalah sebagai berikut :
Dari data yang ada pada tabel tersebut kita akan menggunakan properties pada temperatur 350K dan 400K untuk melakukan interpolasi. Data tersebut kita input ke aplikasi modelica dengan tambahan kata "parameter real" di depan.
Setelah itu kita input data yang akan di hitung menggunakan kata "real" didepan data yang akan kita cari, lalu masukan persamaan yang akan digunakan untuk menghitung interpolasi berikut. Persamaan nya berupa (y-y1)/(y2-y1) = (x-x1)/(x2-x1)
Setelah itu kita simulasikan untuk mendapatkan hasil dari persamaan tersebut , sehingga mendapatkan angka sebagai berikut
Untuk penjelasan lebih lengkapnya saya cantumkan dalam video berikut :
https://www.youtube.com/watch?v=Sr8kFdFIm_o
Pertemuan Metode Numerik 2 : 16 November 2020
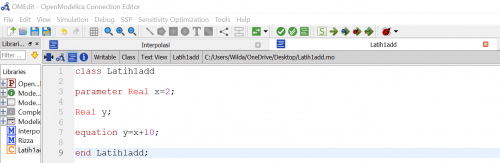
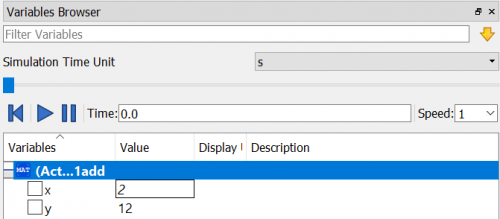
Pada pertemuan kedua kami semua diperintahkan untuh mencoba melakukan simulasi simpel yaitu menjumlahkan suatu variabel dengan angka 10 ( y = x + 10 ). Hal yang pertama dilakukan adalah menginput parameter real yaitu berupa nilai x = 2, setelah itu kita menginput real yaitu berupa variabel yang nilai nya akan ditentukan, kemudian dilanjutkan dengan menginput equation atau persamaan y = 10 + x.
Setelah itu kita melakukan simulasi dan dihasilkan hasil sebagai berikut :
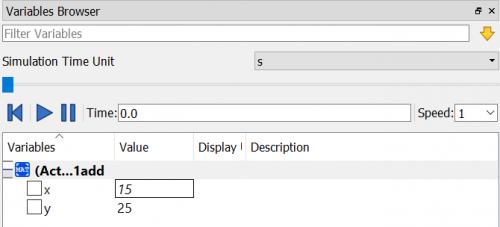
Setelah disimulasi kita masih bisa mengubah variabel x dengan nilai berapapun, dan melalukan simulasi ulang / resimulate sehingga akan menghasilkan nilai yang berbeda. Contohnya saya akan mengubah variabel x = 15 dan saya tunjukan pada gambar berikut
PR 2 Aljabar Simultan dengan OpenModelica
Pada petemuan kedua pak Dai memberikan PR kepada mahasiswa yaitu membuat class dengan type function untuk menyelesaikan persamaan aljabar simultan (metoda gauss elimination, gauss seidel ataupun metoda lain dan sebuah class untuk menjalankan fungsi tersebut. Dari PR yang diberikan saya akan mencoba menggunakan metode gauss elimination untuk mendapatkan solusi dari persamaan berikut dengan menggunakan aplikasi openmodelica
w + 2x - y + z = 6
-w + x + 2y - z = 3
2w - x + 2y + 2z= 14
w + x - y + 2z= 11
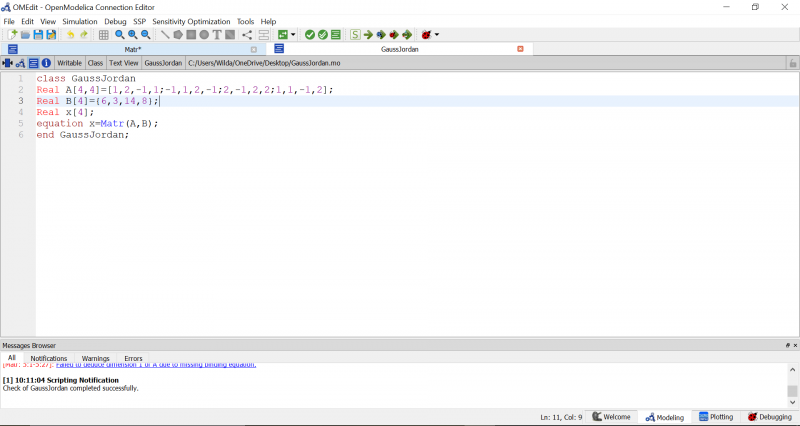
Dari persamaan berikut saya modelkan ke aplikasi openmodelica menggunakan bantuan fungsi solve
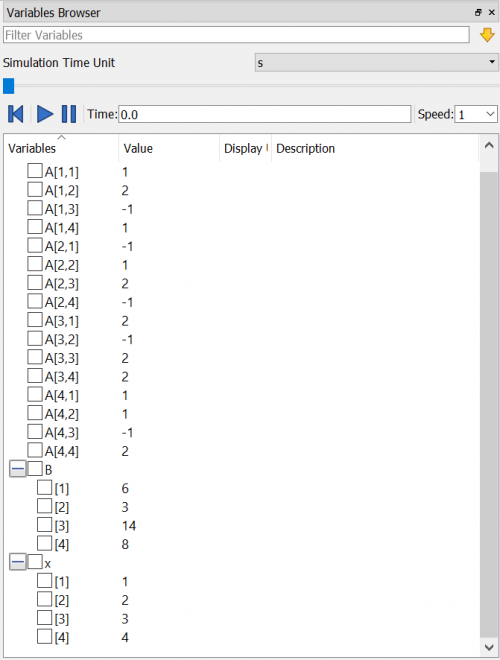
Setelah itu saya membuat class dengan dengan meng input koefisien persamaan diatas kedalam bentuk matrix
Setelah itu dilakukan simulasi sehingga mendapatkan hasil sebagai berikut
Pertemuan Metode Numerik 3 : 23 November 2020
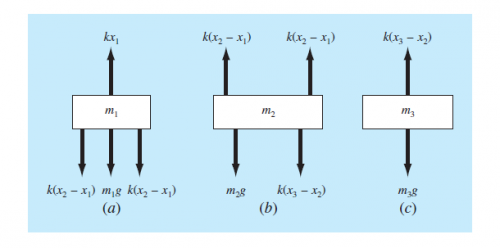
Pada pertemuan ketiga pak DAI memerintahkan semua mahasiswa untuk mencoba membuktikan hasil deltaX dari suatu sistem pegas yang ada didalam buku Steven C Chapra pada sub bab 12.4 dengan free body diagram sistem sebagai berikut :
Karena sistem berada dalam kondisi statis maka m d^2x/dt^2 = 0. Sehingga menghasilkan persamaan sebagai berikut
Data yang diketahui dari soal adalah sebagai berikut
k = 10N/m m1 = 2kg m2 = 3kg m3 = 2.5
Dengan mensubstitusi semua besaran yang diketahui ke persamaan total maka akan didapatkan matrix sebagai berikut
Dari persamaan berikut saya modelkan ke aplikasi openmodelica menggunakan bantuan fungsi solve dengan persamaan dasar W = K * x
Dari matrix yang telah didapat, input ke dalam class openmodelica
Setelah itu semua disimulasi akan mendapatkan nilai x1, x2 dan x3 sebagai berikut
Dan hasil dari perhitungan di buku adalah sebagai berikut
Dari kedua hasil perhitungan diatas dapat disimpulkan bahwa hasil dari perhitungan di buku dan open modelica mempunyai hasilyang sama.
PR 3 Menghitung Dispalcement dan Gaya Reaksi pada Balconi Truss dengan OpenModelica
Pada petemuan kedua pak Dai memberikan PR kepada mahasiswa yaitu menghitung dispalcement dan gaya reaksi pada balconi truss dengan OpenModelica.
Dari PR yang diberikan saya akan mencoba menggunakan aljabar simultan untuk mencari nilai displacement dan gaya reaksi disetiap join. Hal yang pertama dilakukan adalah menentukan node, sudut terhadap sumbu X positif dan element pada setiap batang.
Setelah itu kita menentukan kekakuan setiap batang dengan rumus k = AE/L. Untuk hal itu kita harus menentukan luas penampang dan panjang setiap batang. Dari soal sudah diketahui modulus elastisitas setiap batang E = luas penampang setiap batang sebesar 8inch persegi dan panjang batang 1, 3, 4 dan 6 adalah 3 feet atau sebesar 36 inch dan sudut antara batang 4 dengan batang 2 dan 5 adalah 45 derajat. Oleh karena itu kita dapat menghitung panjang batang 2 dan 5 dengan 36/cos45 = 50.9 inch. Sehingga k untuk batang 1, 3, 4 dan 6 adalah
dan K untuk batang 2 dan 5 adalah :
Setelah itu kita membuat persamaan K dalam bentuk matrix untuk setiap elemen.Dengan rumus sebagai berikut
Analisa Batang 1, 3 dan 6
K matrix untuk element digunakan dengan cara menginput setiap sudut yang terbentuk pada batng ke dalam marix. Karena batang 1,3 dan 6 pada mempunyai K = 4,22 x 10^5 dan sudut 0 terhadap sumbu X maka ketiga pada batang tersebut mempunyai matrix K sebagai berikut :
Lalu diaplikasikan ke batang 1, 3 dan 6
Lalu ketiga matrix tersebut diinput ke dalam matrix global sesuai dengan posisi U
Analisa Batang 4
Batang 4 mempunyai K = 4,22 x 10^5 dan sudut 90 derajat terhadap sumbu X maka ketiga pada batang tersebut mempunyai matrix K sebagai berikut :
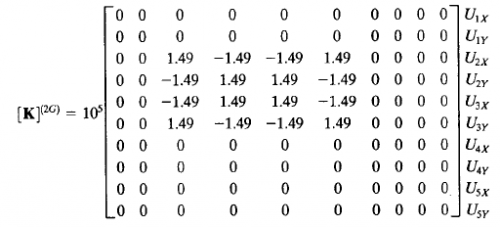
Lalu matrix tersebut diinput ke dalam matrix global sesuai dengan posisi U
Analisa Batang 2
Batang 2 mempunyai K = 2,98 x 10^5 dan sudut 135 derajat terhadap sumbu X maka ketiga pada batang tersebut mempunyai matrix K sebagai berikut :
Lalu matrix tersebut diinput ke dalam matrix global sesuai dengan posisi U
Analisa Batang 5
Batang 5 mempunyai K = 2,98 x 10^5 dan sudut 45 derajat terhadap sumbu X maka ketiga pada batang tersebut mempunyai matrix K sebagai berikut :
Lalu matrix tersebut diinput ke dalam matrix global sesuai dengan posisi U
Kemudian kita menjumlahkan semua matrix K global tersebut menjadi matrix K global total
Sehingga akan menjadi hasil seperti berikut
Tentukan kondisi batas dan kondisi pembebanan pada struktur. Dari struktur kita dapat mengetahui bahwa U1x, U1y, U3x, U3y = 0 dan beban sebesar 500 kearah bawah pada titik tumpuan 4 dan 5 ke arah sumbu Y. Karena nilai U1x, U1y, U3x, U3y = 0 maka kita bisa mengeliminasi baris dan kolom 1, 2, 6 dan 7, sehingga nantinya akan didapatkan matrix berukuran 6 x 6.
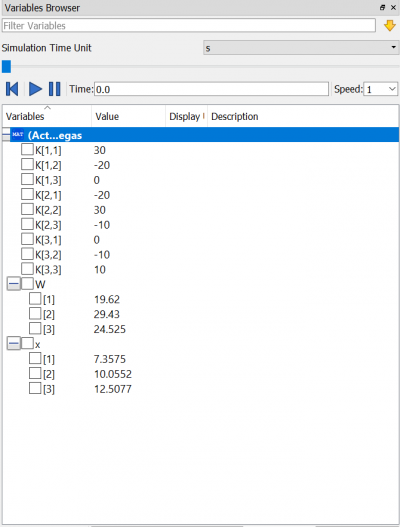
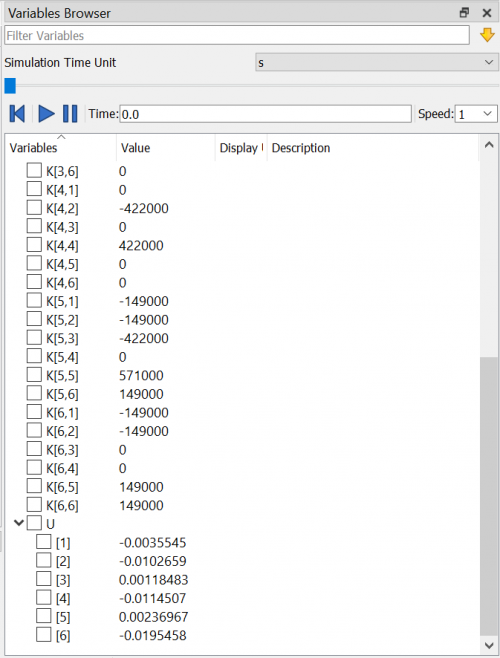
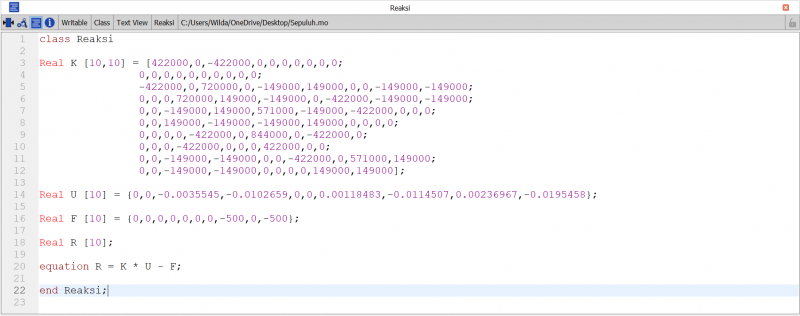
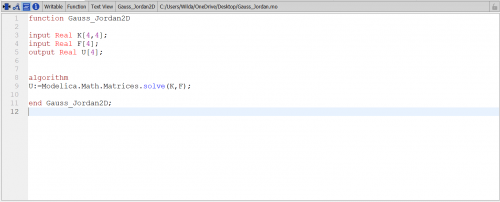
Setelah itu kita akan menghitung nilai U menggunakan simulasi pada aplikasi OpenModelica. Saya menggunakan konsep eliminasi gauss jordan dengan menginput nilai K dan F untuk mendapatkan nilai U. Berikut adalah fungsi dan class nya
Hasil dari simulasi OpenModelica adalah
U2x = -0.0035545 inch
U2y = -0.0102659 inch
U4x = 0.00118483 inch U4y = -0.0114507 inch
U5x = 0.00236967 inch
U5y = -0.0195458 inch
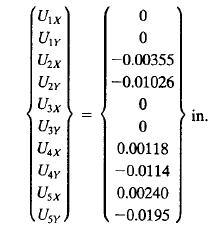
Karena nilai U1x, U1y, U3x, U3y = 0, komponen U jika disusun akan menjadi seperti berikut
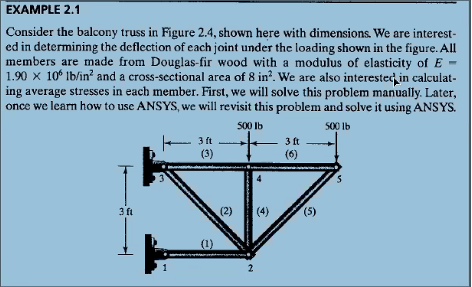
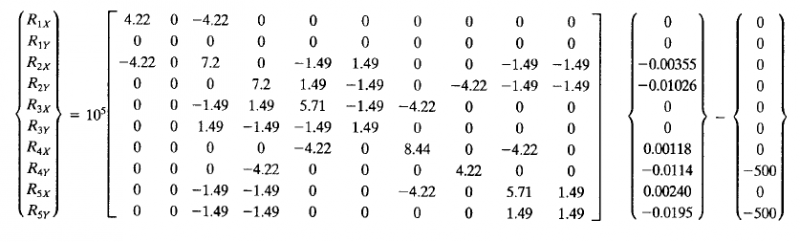
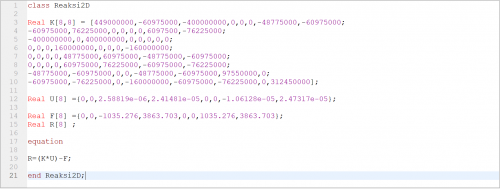
Setelah nilai U didapatkan, kita dapat menghitung besarnya gaya reaksi disetiap titik tumpuan dengan rumus R = Kglobal*U - F dalam bentuk matrix
Setelah itu kita akan menyelesaikan persamaan matrix tersebut menggunakan Openmodelica menggunakan class sebagai berikut
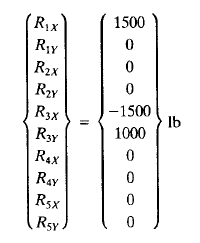
Sehingga menghasilkan nilai R sebagai berikut
Pada hasil dibuku nilai nilai R tersebut mengalami pembulatan, sehingga hasilnya menjadi seperti berikut
Pertemuan Metode Numerik 4 : 30 November 2020 Quiz 1
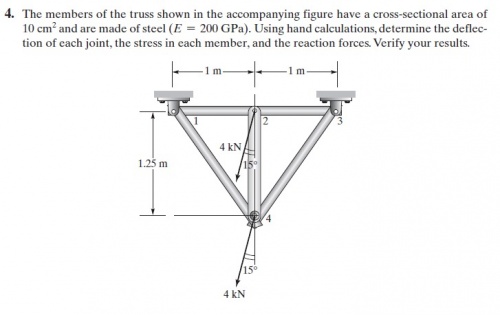
Pada pertemuan kali ini kami semua diberikan soal quiz oleh pak Dai . Soalnya adalah seperti berikut
Pertama kami diminta untuk membuat flowchart untuk proses pengerjaan soal. Flowchart yang digunakan untuk kedua soal ini sama, yaitu:
Pertama yang harus dilakukan adalah membuat tabel, berisi nama element, node, dan sudut setiap batang terhadap sumbu X positif. Setelah itu menentukan nilai kekakuan pada setiap batang.
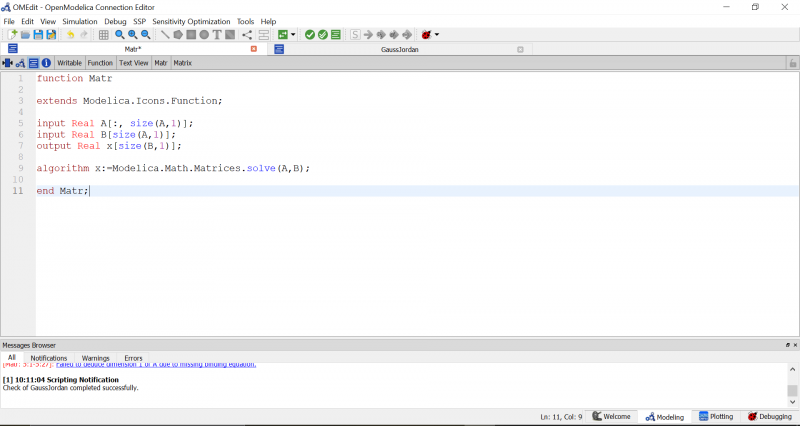
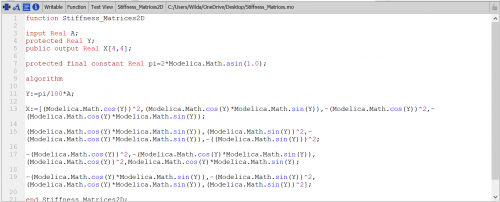
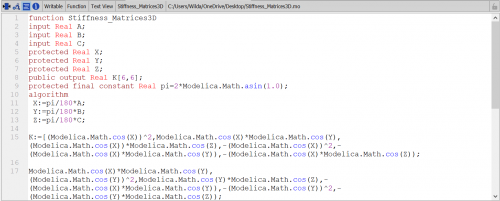
Setelah itu kita membuat K lokal untuk setiap batang menggunakan fungsi dan class pada OpenModelica
Setelah didapatkan nilai K lokal, kita konversi menjadi K global pada setiap batang. Kemudian nilai K pada setiap batang ini dijumlahkan menjadi K global total. Disini saya menggunakan perhitungan manual menggunakan bantuan excel, sehingga menghasilkan sebagai berikut.
Setelah dimasukan kondisi batas Ux1, Uy1, Ux3, Uy3 = 0. Maka matrixnya akan menjadi berukuran 4 x 4
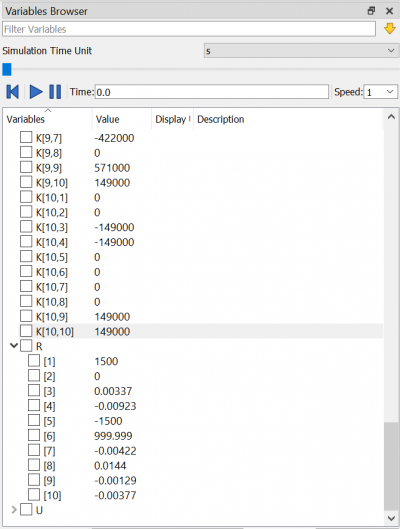
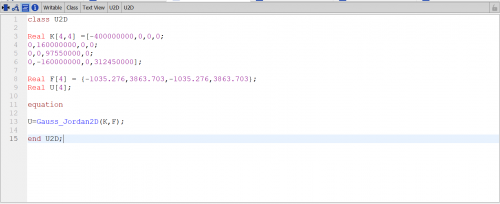
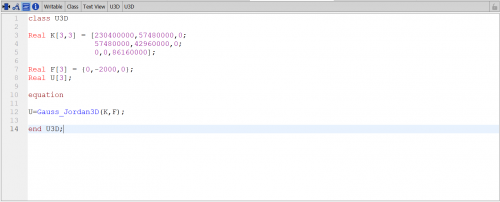
Sehingga untuk U dan R nya menjadi seperti berikut :
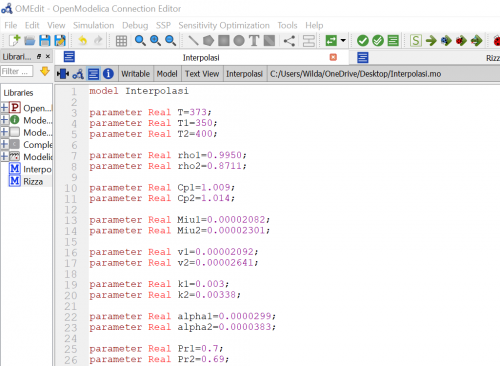
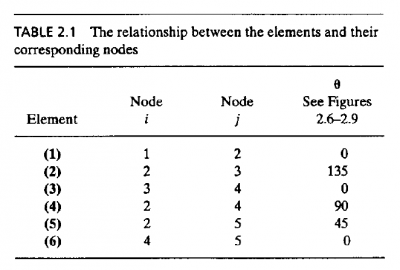
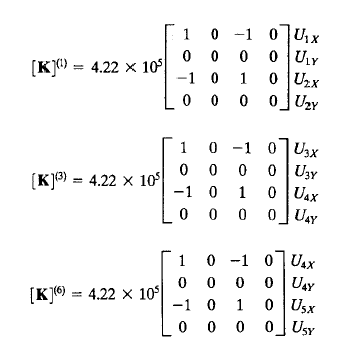
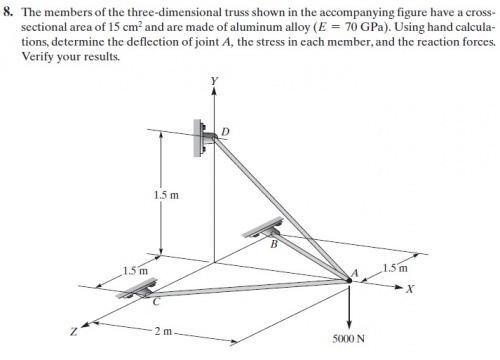
NO.8
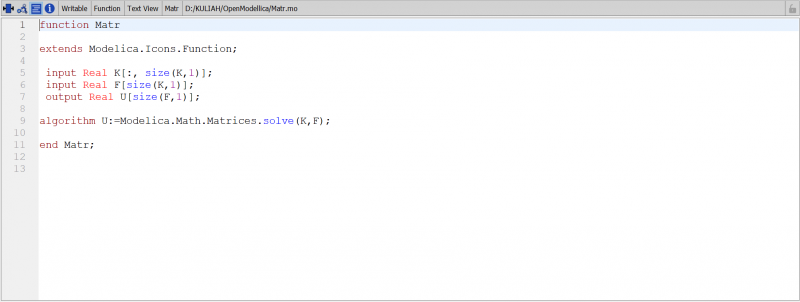
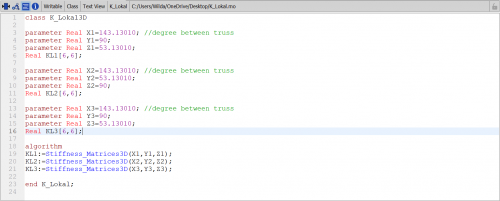
Pertama yang harus dilakukan adalah membuat tabel, berisi nama element, node, dan sudut setiap batang terhadap sumbu X positif. Setelah itu menentukan nilai kekakuan pada setiap batang.
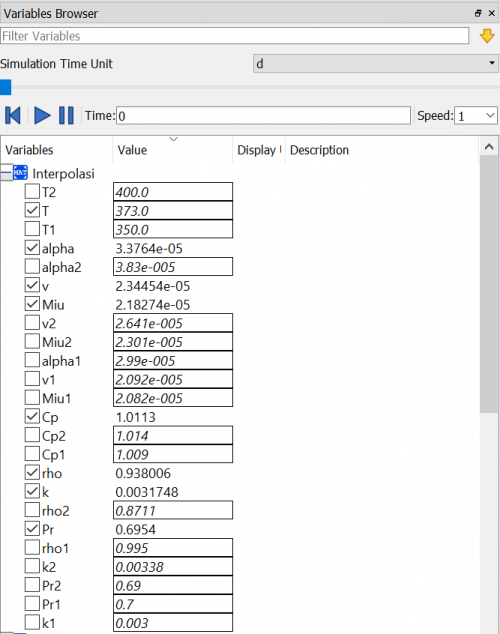
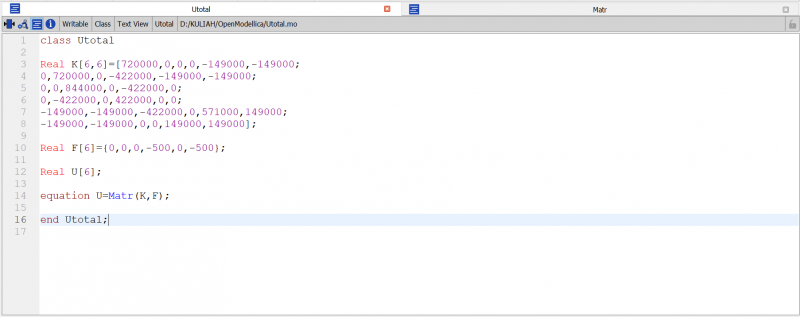
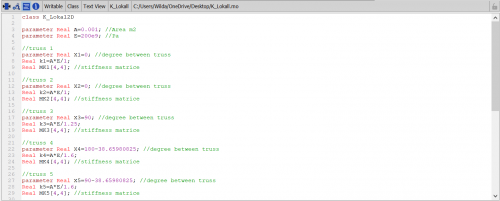
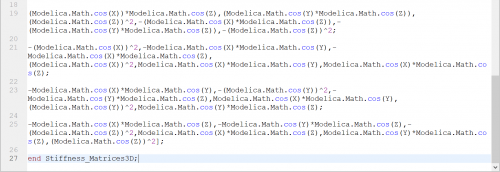
Setelah itu kita membuat K lokal untuk setiap batang menggunakan fungsi dan class pada OpenModelica
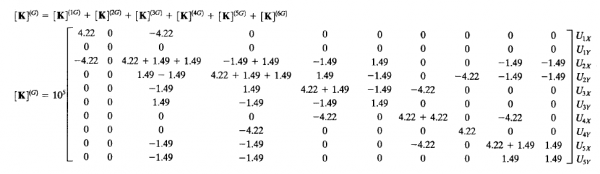
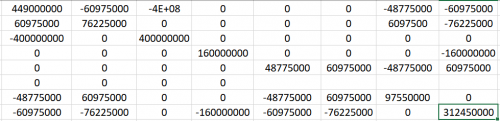
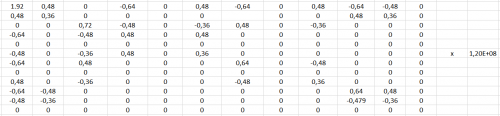
Setelah didapatkan nilai K lokal, kita konversi menjadi K global pada setiap batang. Kemudian nilai K pada setiap batang ini dijumlahkan menjadi K global total. Disini saya menggunakan perhitungan manual menggunakan bantuan excel, sehingga menghasilkan sebagai berikut.
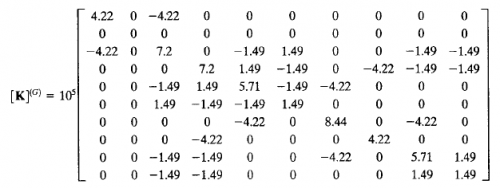
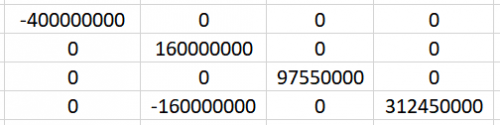
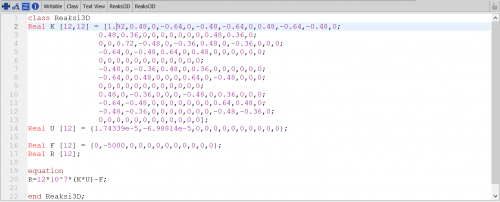
Setelah dimasukan kondisi batas UxB, UyB, UzB, UxC, UyC, UzC, UxD, UyD, UzD= 0. Maka matrixnya akan menjadi berukuran 3 x 3
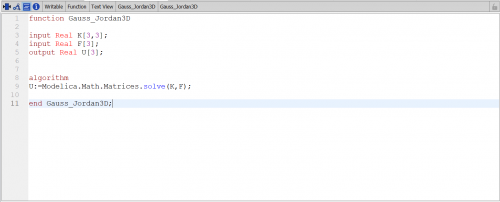
Sehingga untuk U dan R nya menjadi seperti berikut :