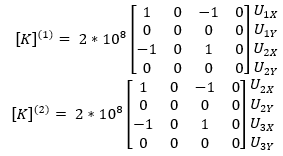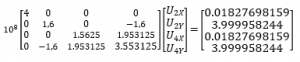Difference between revisions of "Metnum03-Samuel Sitompul"
| Line 174: | Line 174: | ||
U2X=0,018277 ; U2Y=3.99996 ; U4X=0,018277 ; U4Y=3.99996 | U2X=0,018277 ; U2Y=3.99996 ; U4X=0,018277 ; U4Y=3.99996 | ||
| + | |||
| + | lalu untuk mencari gaya reaksi, digunakan persamaan | ||
| + | |||
| + | R=[K]{U}-{F} | ||
| + | |||
| + | berikut penyelesaian menggunakan openmodelica | ||
| + | |||
| + | [[File:Gaya reaksi.png|500px]] | ||
| + | |||
| + | terdapat permasalahan pada software openmodelica yang belum bisa saya temui pemecahannya, sehingga tidak dapat menyelesaikan persamaan tersebut. | ||
Revision as of 10:37, 7 December 2020
Contents
Biodata
Nama: Samuel Albert B C H Sitompul
NPM : 1606907556
Hobi: Membaca Buku
Pertemuan Minggu Pertama Metode Numerik 03 (9 November 2020)
Pertemuan Minggu Kedua Metode Numerik 03 (16 November 2020)
Pada pertemuan kedua kali ini, Kami diminta oleh Pak Dai untuk menunjukkan pemahaman kami mengenai tugas minggu lalu, yaitu mempelajari OpenModelica. Lalu kami melakukan simulasi dengan membuat program sederhana didalam OpenModelica untuk menjumlahkan 10 angka pada variabel.
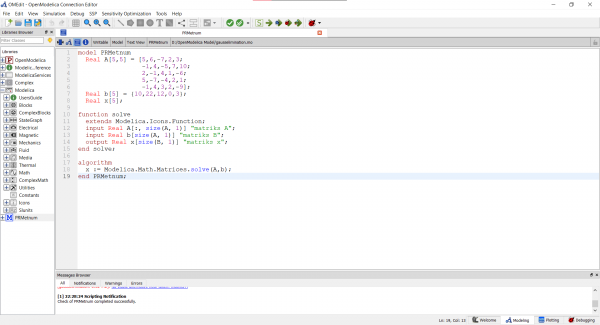
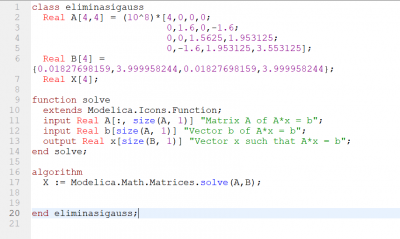
Setelah kelas, Pak Dai memberikan tugas kepada kita untuk membuat simulasi untuk menyelesaikan persamaan aljabar simultan (bisa metode eliminasi gauss, metode gauss seidel, dsb.) Berikut adalah hasil percobaan saya untuk menyelesaikan sistem persamaan aljabar. Untuk simulasi ini, saya menggunakan metode eliminasi gauss untuk menyelesaikan permasalahan aljabar simultan.
Metode eliminasi gauss merupakan salah satu metode dalam menyelesaikan sebuah sistem persamaan dengan mengubah sistem persamaan tersebut kedalam bentuk matrix. Setelah diubah, lalu matrix yang berisi angka dipindah-ruaskan lalu diselesaikan sehingga didapat nilai-nilai dari variabel yang kita cari.
Berikut adalah model simulasi yang saya buat:
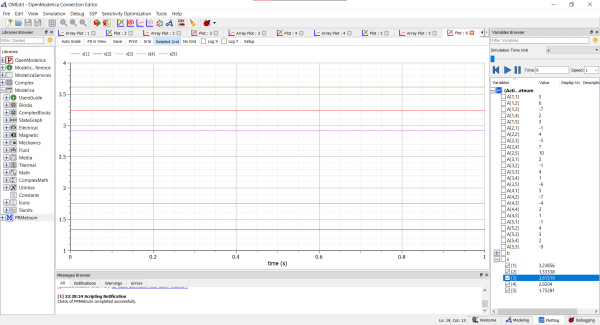
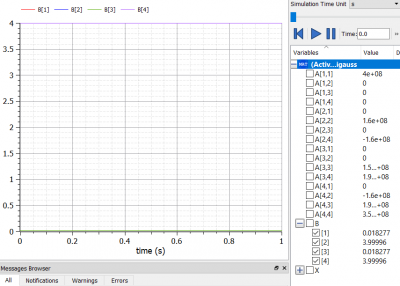
Saya mencoba menyelesaikan 5 sistem persamaan linier dengan metode eliminasi gauss dengan perintah "Modelica.Math.Matrices.solve(A,b)". Setelah melakukan pengecekan model, saya menjalankan simulasi dan melakukan plotting seusai simulasi. Berikut adalah hasil plotting tersebut:
dapat dilihat bahwa tiap garis menunjukkan penyelesaian dari sistem persamaan tersebut. Terdapat 5 solusi dari 5 sistem persamaan dengan 5 variabel
Pertemuan Minggu Ketiga Metode Numerik 03 (23 November 2020)
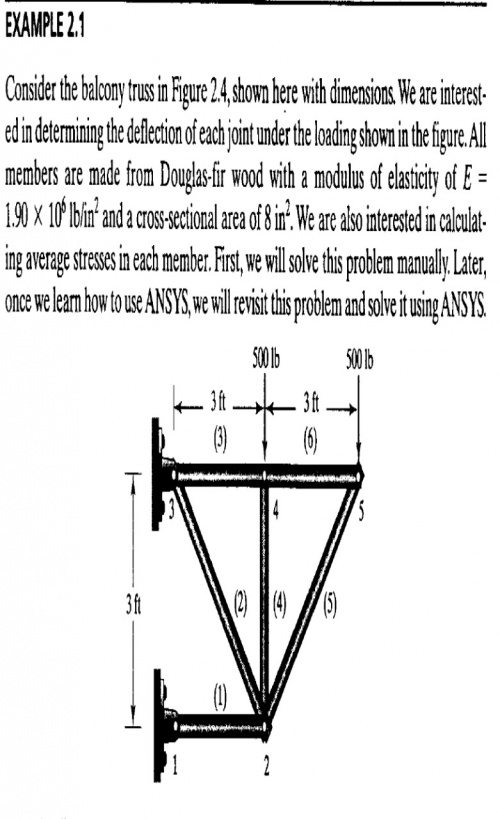
Di pertemuan hari ini, Pak Dai menjelaskan tentang aplikasi metode numerik untuk permasalahan-permasalahan teknik. Salah satunya adalah permasalahan sistem pegas-massa.
Setelah kelas, Pak Dai memberikan tugas untuk menyelesaikan soal berikut:
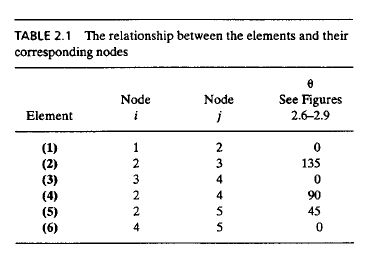
Untuk menyelesaikan soal ini perlu dilakukan pengelompokan menjadi node dan elemen seperti pada tabel berikut:
lalu perlu dilakukan perhitungan nilai kekakuan pada elemen. Untuk elemen 1,3,5, dan 6 nilai kekakuannya adalah 4,22 x 10^5 lb/in. sedangkan untuk elemen 2, dan 4 nilai kekakuannya adalah 2,98 x 10^5 lb/in.
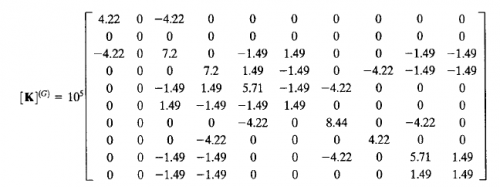
setelah itu perlu dilakukan analisis kekakuan pada tiap elemen dalam matriks koordinat global, kemudian dijumlahkan untuk mendapatkan K global. berikut adalah hasil penjumlahan dari nilai kekakuan tiap elemen:
disederhanakan menjadi
setelah mendapat matriks kekakuan, diterapkan kondisi batas dan beban. Untuk node 1 dan 3 adalah fixed, maka U1X=0, U1Y=0, U3X=0, U3Y=0 dan beban diberikan pada node 4 dan 5 sebesar F4Y= -500lb dan F5Y= -500lb
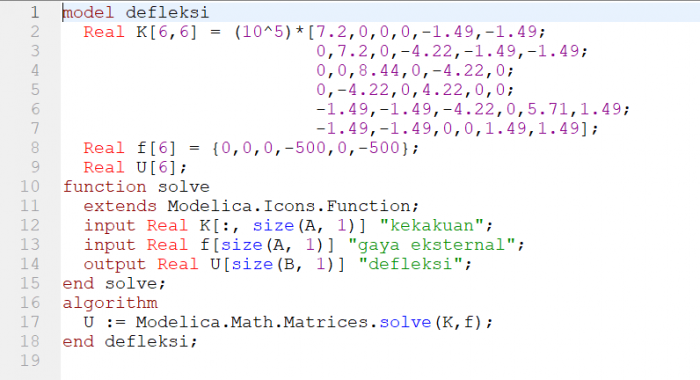
dengan menggunakan Hukum Hooke yaitu F=k.x, maka didapatkan persamaan defleksi menjadi
Persamaan diatas kemudian diselesaikan dengan OpenModelica, berikut saya lampirkan coding yang saya buat
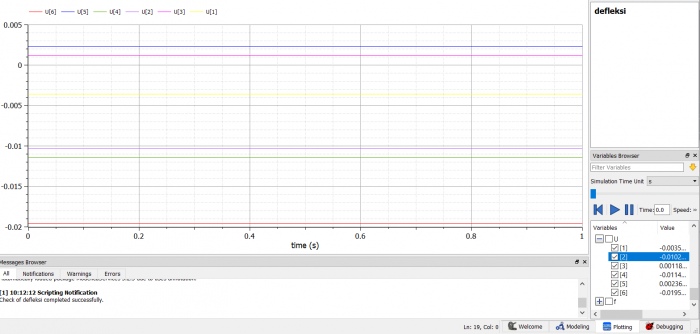
setelah melakukan pengecekan dan simulasi, saya melakukan plotting. berikut hasil plotting simulasi tersebut.
hasil dapat dilihat pada panel di bagian kanan bawah gambar.
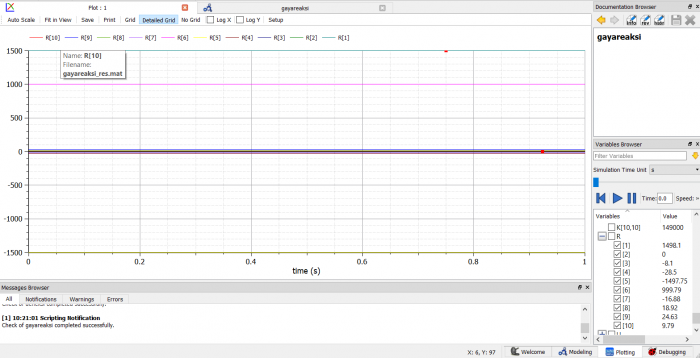
Untuk mendapatkan gaya reaksi, persamaannya adalah:
{R}=[K].{U}-{F}
diterapkan matriks-matriks yang sudah diketahui, didapat:
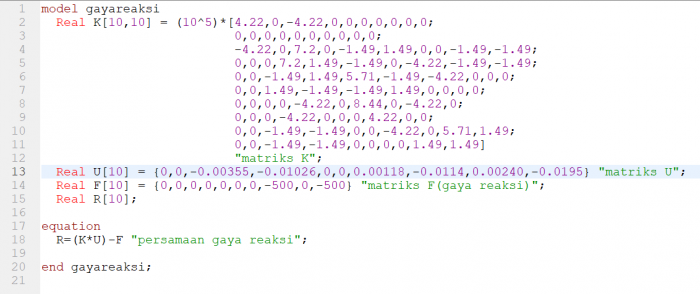
Persamaan diatas dapat diselesaikan oleh openmodelica. berikut adalah coding yang saya buat
hasil simulasi tersebut di plot sebagai berikut:
nilai R tiap node dapat dilihat di bagian kanan bawah gambar
QUIZ I METODE NUMERIK (30 November 2020)
Pada pertemuan minggu ke IV hari ini, Pak Dai mengadakan kuis untuk menguji kemampuan inidvidu kami, para peserta diberikan 2 buah soal kuis dan diminta untuk menuliskan flowchartynya. Berikut merupakan kedua soal kuisnya.
dan berikut merupakan tampilan flowchart pengerjaan sebagai jawaban soal kuis tersebut yang telah saya buat. Mengingat alur pengerjaan kedua soal tersebut hampir sama, maka tampilan flowchart tersebut merepresentasikan keduanya.
Tugas
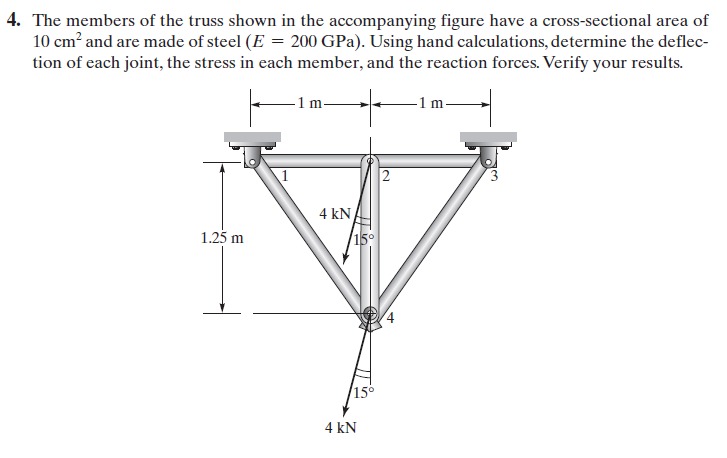
Soal no.4
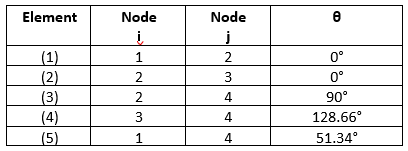
untuk soal nomor 4, langkah pertama yang dilakukan adalah mendefinisikan node dan elemen sebagai berikut
Lalu mencari nilai kekakuan dari tiap elemen
- elemen 1,2
k=AE/L=(10 x 10^-4)(200 x 10^9)/1= 2 x 10^8
- elemen 3
k=AE/L=(10 x 10^-4)(200 x 10^9)/1,25= 1,6 x 10^8
- elemen 4,5
k=AE/L=(10 x 10^-4)(200 x 10^9)/1,6= 1,25 x 10^8
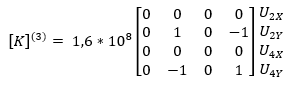
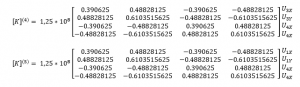
Lalu membuat matriks kekakuan untuk tiap elemen
- elemen 1,2
- elemen 3
- elemen 4,5
setelah membuat matriks lokal, diubah menjadi matriks global
setelah membuat matriks global, dilakukan penjumlahan untuk semua matriks global
diketahui kondisi batas:
U1X=0, U1Y=0, U3X=0, U3Y=0
diketahui gaya eksternal di titik 2 dan 4
F2X=F4X=0.01827698159; F2Y=F4Y=3.999958244
dengan persamaan F=k.x, maka didapatkan
namun karena pada titik 1 dan 3 tidak bergerak, maka baris dan kolom 1,2,5,6 dihilangkan
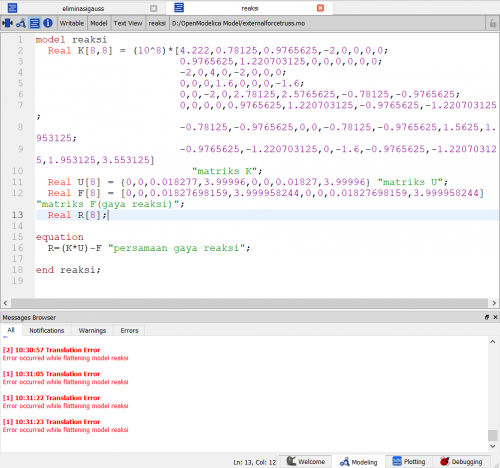
persamaan diatas lalu diselesaikan dengan metode eliminasi gauss oleh openmodelica
U2X=0,018277 ; U2Y=3.99996 ; U4X=0,018277 ; U4Y=3.99996
lalu untuk mencari gaya reaksi, digunakan persamaan
R=[K]{U}-{F}
berikut penyelesaian menggunakan openmodelica
terdapat permasalahan pada software openmodelica yang belum bisa saya temui pemecahannya, sehingga tidak dapat menyelesaikan persamaan tersebut.