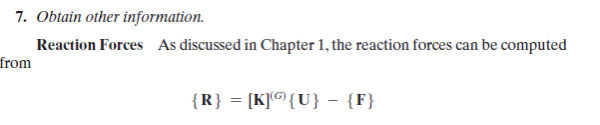Difference between revisions of "Hikaru Trinita Salsabila"

From ccitonlinewiki
Jump to: navigation, search
(→‎Minggu 3 (25 November 2018))
Line 102: Line 102:
 
[[File:HIkaru 9.4.png|720px|center]]
 
[[File:HIkaru 9.4.png|720px|center]]
 
Kemudian, pseudocode tersebut dibuat kedalam bahasa Open  Modelica:
 
Kemudian, pseudocode tersebut dibuat kedalam bahasa Open  Modelica:
 +
 +
'''NaiveGauss.mo'''
 +
function NaiveGauss
 +
 +
input Real [3,3] A;
 +
input Real [3] B; 
 +
output Real [3] x; 
 +
protected
 +
Real [3,3] a;
 +
Real [3] b;
 +
Integer m = size(A,1); // jumlah kolom
 +
Integer n = size(A,2); // jumlah baris
 +
Real k = 1;     
 +
Real i = 1;     
 +
Real j = 1;     
 +
Real factor = 1;
 +
Real sum = 1; 
 +
 
 +
algorithm
 +
a := A;
 +
b := B;
 +
// Forward Elimination
 +
for k in 1:(n-1) loop
 +
  for i in (k+1):n loop
 +
    factor := a[i,k] / a[k,k];
 +
    for j in (k+1):n loop
 +
      a[i,j] := a[i,j] - (factor * a[k,j]);
 +
    end for;
 +
    b[i] := b[i] - (factor * b[k]);
 +
  end for;
 +
end for;
 +
// Back Substitution
 +
x[n] := b[n] / a[n,n];
 +
for i in (n-1):(-1) loop
 +
  sum := b[i];
 +
  for j in (i+1):n loop
 +
    sum := sum - (a[i,j] * x[j]);
 +
  end for;
 +
  x[i] := sum / a[i,i];
 +
end for;
 +
 +
end NaiveGauss;
 +
 
[[File:Hikaru 9.5-1.png|720px|center]]
 
[[File:Hikaru 9.5-1.png|720px|center]]
 
Function Naïve Gauss yang sudah dibuat tersebut dibuktikan dengan menyelesaikan example 9.5 pada buku Chapra:
 
Function Naïve Gauss yang sudah dibuat tersebut dibuktikan dengan menyelesaikan example 9.5 pada buku Chapra:

Revision as of 11:18, 2 December 2020

Biodata

IMG-20191103-WA0193.jpg

Nama  : Hikaru Trinita Salsabila

NPM  : 1806149122

TTL  : Kawasaki, 25 Juli 2000

Tempat Tinggal: Depok

Golongan Darah: A

Hobi  : Membaca

Saat ini, saya adalah mahasiswa semester 5 program studi Teknik Mesin Universitas Indonesia. Saya memilih jurusan ini atas saran dari kedua orang tua, yang mana ayah saya juga merupakan dosen di DTM UI. Saya bersyukur bisa menjadi mahasiswa Teknik Mesin Universitas Indonesia, karena kampus ini merupakan salah satu kampus terbaik. Semoga ilmu yang saya dapatkan di perkuliahan bisa menjadi bekal untuk masa depan. Besar harapan agar saya bisa menjadi orang yang bermanfaat bagi diri sendiri dan juga orang lain. Aamiin.


Metode Numerik

Perkuliahan Metode Numerik minggu ke 1-UTS diisi oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. Beberapa topik yang dibahas yaitu:

  • Pseudocode
  • Sistem Persamaan
  • Turunan Numerik
  • Metode Newton Rhapson, Secant, dan Bisection
  • Regresi Linear
  • Interpolasi

Setelah UTS, perkuliahan Metode Numerik diisi oleh Bapak Dr. Ir. Ahmad Indra Siswantara


Minggu 1 (11 November 2020)

Pada pertemuan minggu ini, dipaparkan tujuan-tujuan pembelajaran metode numerik, yaitu: Tujuan:

  • 1.Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik, Contoh:Persamaan aljabar, algorithma, pencocokan kurva, persamaan diferensial parsial, dll.
  • 2.Mengerti aplikasi metode numerik.
  • 3.Mampu menerapkan metode numerik dallam persoalan teknik.
  • 4.Mendapat nilai tambah/adab sehingga kita menjadi orang yang lebih beradab.

Tugas Minggu 1

Untuk tugas pertama, kami diminta mempelajari Open Modelica, yaitu sebuah aplikasi untuk membuat modelling dan simulasi. Aplikasi ini biasa digunakan digunakan di bidang industri maupun akademis. Untuk mempelejari aplikasi tersebut, saya menonton beberapa video dari youtube:

Saya mencoba membuat model sederhana yaitu sistem katrol(untuk mencari nilai tegangan tali dan percepatan) dan interpolasi (untuk mencari nilai diantara dua buah nilai yang sudah diketahui). Video pembelajaran adalah sebagai berikut:

  • Sistem Katrol Tetap
  • Interpolasi

Minggu 2 (18 November 2020)

Di awal pertemuan disampaikan oleh Pak Dai, jika kita sebagai manusia harus memiliki perubahan setiap harinya, hari ini harus lebih baik dari hari kemarin. Sebelum memasuki materi, kami diminta mereview fungsi pembelajaran aljabar linear dan hubungannya dengan metode numerik. Kemudian, kami diminta menceritakan pengalaman mempelajari aplikasi Open Modelica. Aplikasi ini dibuat dengan tujuan bahasa pemodelan, bukan coding. Akan tetapi, ketika melakukan perhitungan, code yang ditulis harus dalam bahsa C++. Salah satu alasan pemilihan penggunaan aplikasi ini adalah karena Open Modelica dibuat free, sehingga bisa digunakan oleh siapa saja. Open Modelica mempunyai beberapa fitur, seperti membuat model, class, function, dan lain-lain. Aplikasi ini object oriented, kita bisa membuat beberapa class fungsi dan class eksekusi, kemudian menggabungkannya menjadi satu model.

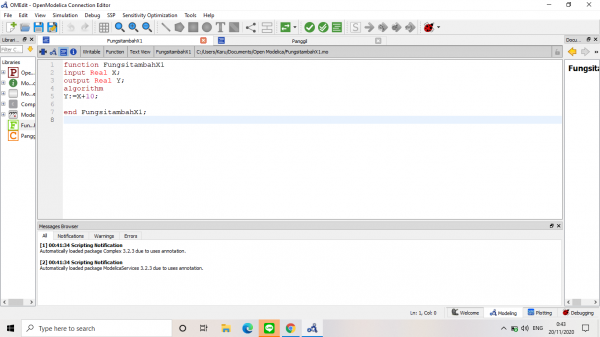
Sebagai contoh pembelajaran, kami dipandu oleh Pak Dai membuuat sebuah function dan class yang akan dihubungkan. Function yang dibuat adalah "Fungsi Tambah X1"dengan X sebagai input, Y sebagai output, dan fungsi yang dibuat adalah Y=10+x. Dibuat dalam Open Modelica sebagai berikut:

Fungsitambahx1.png

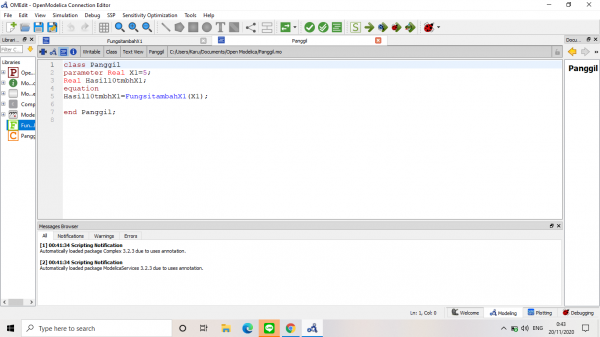
Selanjutnya dibuat class "Panggil"yang berfungsi "memanggil" fungsi tambah X1 tersebut. Pada class ini, kita dapat mengubah-ubah nilai input X1.

Classpanggil.png

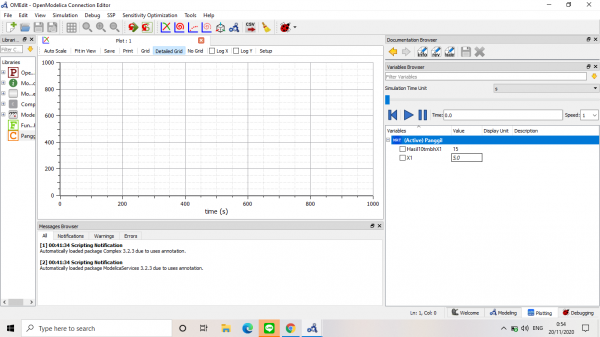
Dengan gabungan class dan function ini, kita dapat mencari nilai output Y dengan memasukkan nilai input X1. Sebagai contoh, dimasukkan nilai X1 sebesar 5 maka sesuai fungsi Y=10+X, akan didapatkan nilai Hasil tambah X1=10+X1=10+5=15.

Hasiltambahx1.png

Nilai X1 dapat diubah-ubah kemudian dilakukan re-simulate untuk mendapatkan nilai outputnya.

Tugas Minggu 2

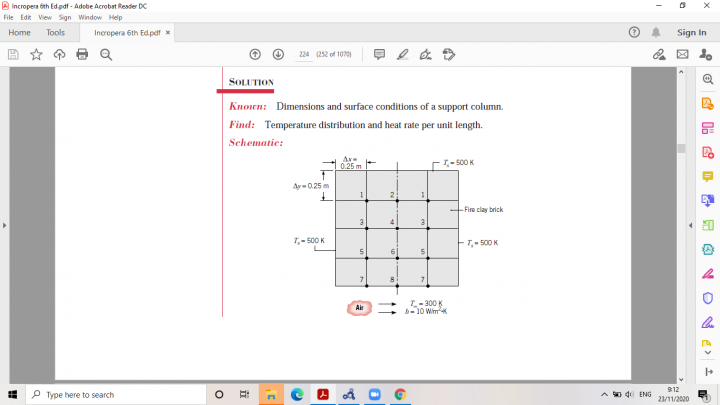
Untuk tugas minggu ini kami diminta membuat sebuah fungsi berupa persamaan aljabar simultan dengan variabel array kemudian membuat class untuk memanggil fungsi tersebut. Persamaan aljabar simultan adalah sebuah persoalan matematika yang kompleks sehingga dengan menggunakan tools, penyelesaiannya dapat dibuat lebih sederhana. Metode yang dapat digunakan untuk menyelesaikan persamaan aljabar simultan adalah metode Gauss, Gauss-Jordan, Crammer, dan Gauss-Seidel. Sedangkan variabel array adalah sebuah variabel yang di dalamnya terdapat banyak data. Sebagai contoh, jika kita memiliki data X1, X2, dan X3, dengan menggunakan variabel array cukup dituliskan X[3] saja. Pada tugas kali ini, saya mencoba menyelesaikan persoalan yang saya ambil dari buku Incropera (mata kuliah Heat Transfer) pada bab 4 mengenai penyelesaian distribusi temperatur pada beberapa node.

Hikaru1.png

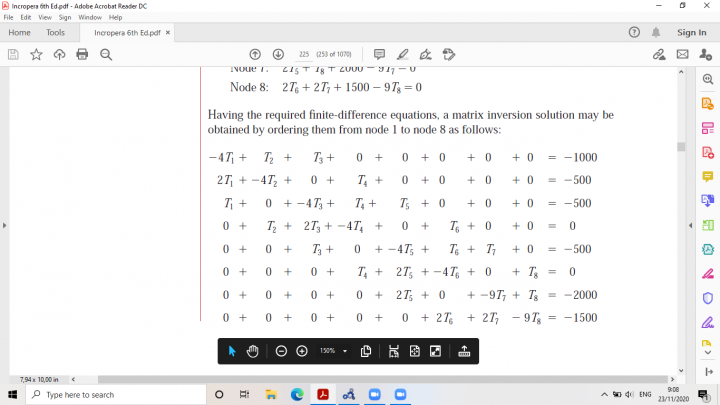
Kemudian persoalan tersebut akan dibuat ke dalam 8 persamaan 8 variabel sebagai berikut:

Screenshot (394).png

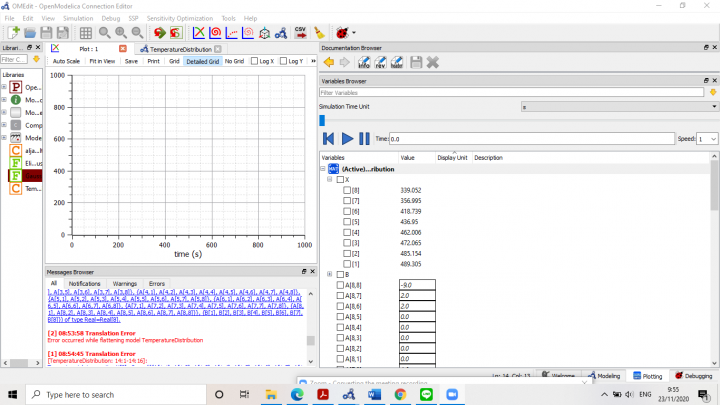
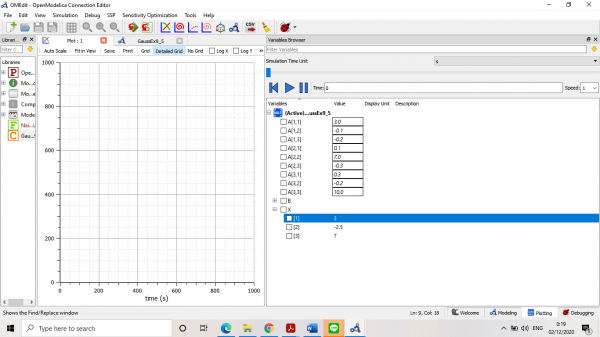
Dengan menggunakan OpenModelica dan metode Gauss, didapatkan hasil T1 hingga T8 yang diwakilkan dengan X:

Screenshot (396).png

Berikut video cara menyelesaikan distribusi temperatur menggunakan Open Modelica:

Minggu 3 (25 November 2018)

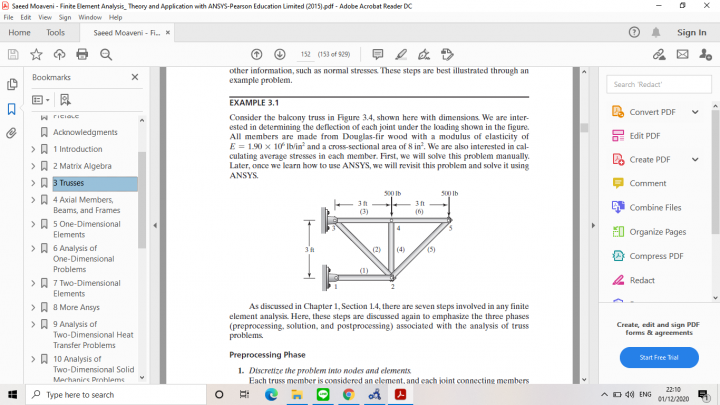
Pada pertemuan minggu ke-3, dibahas aplikasi metode numerik pada permasalahan eknik. Beberapa metode yang dapat digunakan yaitu CFD, Stokastik, dan FEA. Dalam menyelesaikan masalah teknik, angkah yang harus dilakukan adalah melakukan analisis, membuat model matematis, menggunakan metode numerik untuk penyelesain (menggunakan computer), dan didapatkan solusi dari permasalahan. Salah satu permasalahan teknik yang kami pelajari adalah Truss.Sebelum kelas, kami diminta berlatih mengerjakan Example 3.1 mengenai Truss. Berikut example 3.1 yang saya coba kerjakan:

3.1-1.png

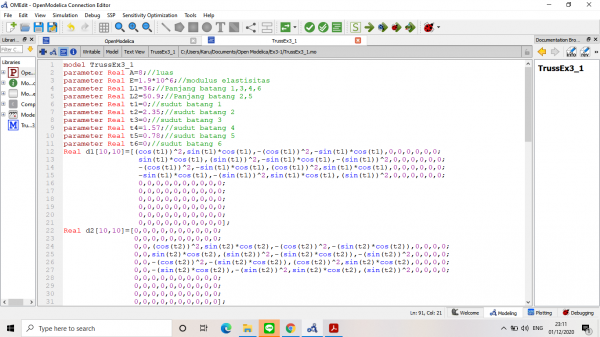
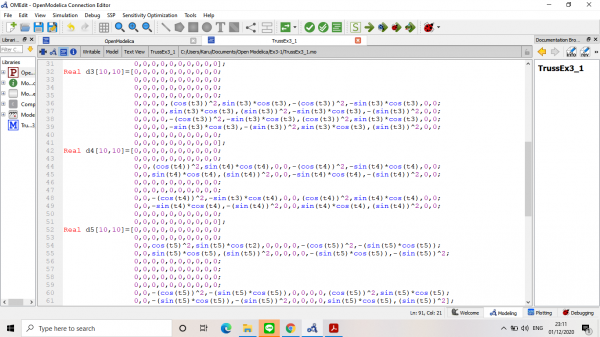
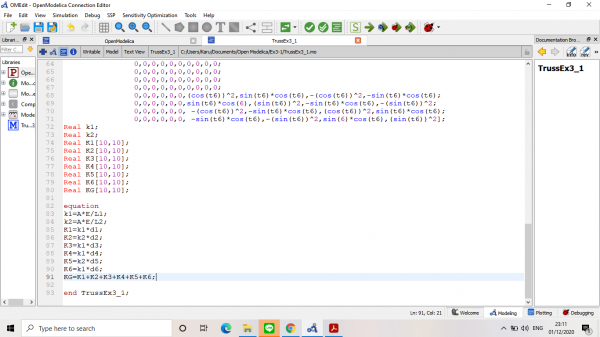
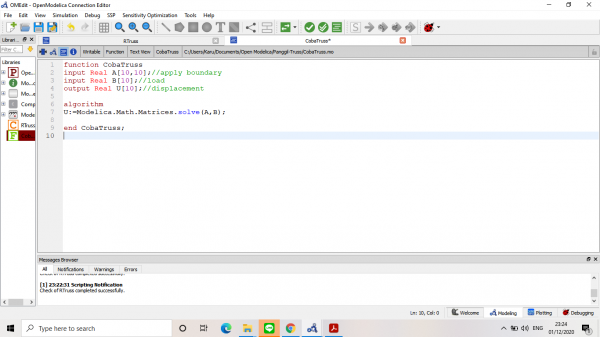
Langkah pertama yaitu mencari matriks kekakuan global dengan code sebagai berikut:

3.1-2.png
3.1-3.png
3.1-4.png

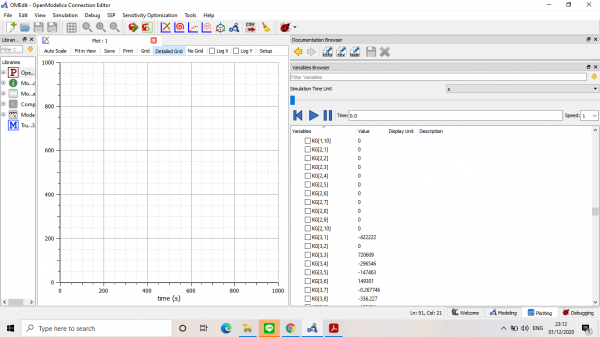
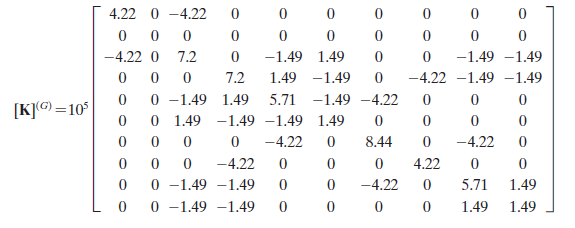
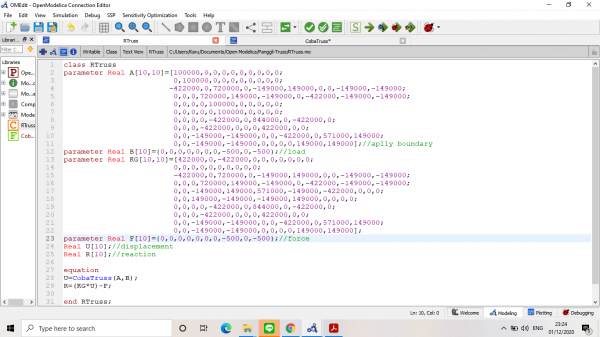
Setelah disimulate, didapatkan nilai-nilai kekakuan global dan dituangkan kedalam matriks:

3.1-5.png
3.1-6.png

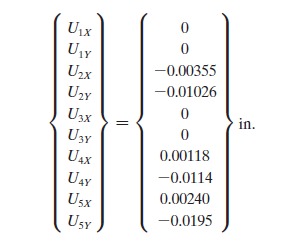
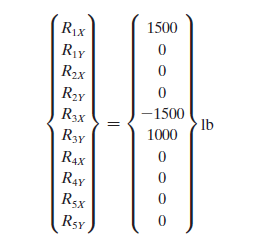
Kemudian, mencari nilai displacement dan reaksi dari truss:

3.1-7.png
3.1-8.png

Persoalan tersebut dibuat kedalam function dan class pada Open Modelica:

3.1-10.png
3.1-11.png

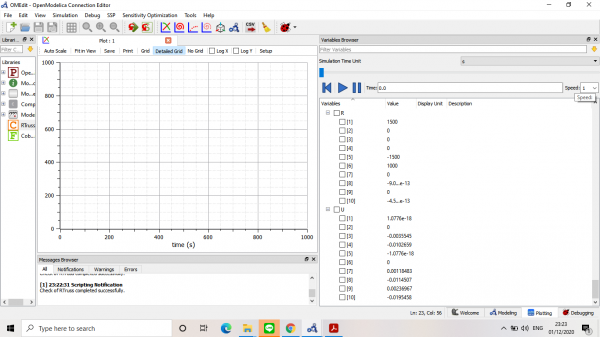
Setelah code tidak ada error, dilakukan simulate dan didapatkan hasil displacement serta reaksi dari truss:

3.1-9.png
Revisi 3.1-12.png
Revisi 3.1-13.png


Ketika kelas, kami kembali dijelaskan mengenai aljabar simultan, variable array, dan metode Gauss. Agar lebih mengerti mengenai aplikasi metode numerik dan pengaplikasiannya dalam Open Modelica, kami diminta membuat code untuk menyelesaikan persamaan 9.12 pada buku Chapra yaitu mengenaik eliminasi Naïve Gauss. Pseudocode untuk eliminasi Naïve Gauss diberikan pada Fig.9.4:

HIkaru 9.4.png

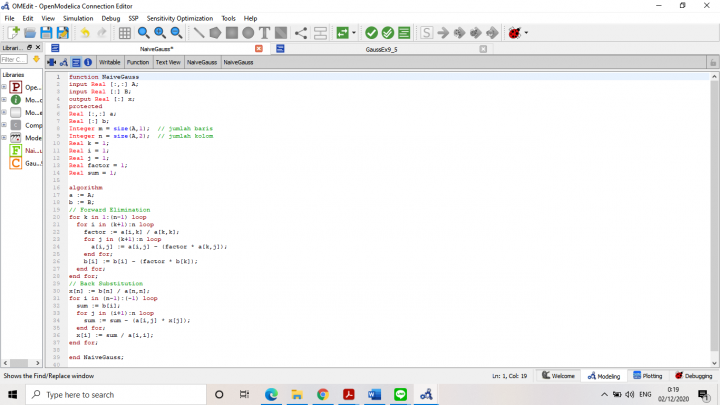
Kemudian, pseudocode tersebut dibuat kedalam bahasa Open Modelica:

NaiveGauss.mo function NaiveGauss 

input Real [3,3] A; 
input Real [3] B;   
output Real [3] x;  
protected
Real [3,3] a;
Real [3] b;
Integer m = size(A,1); // jumlah kolom 
Integer n = size(A,2); // jumlah baris
Real k = 1;      
Real i = 1;       
Real j = 1;       
Real factor = 1; 
Real sum = 1;   
 
algorithm
a := A;
b := B;
// Forward Elimination
for k in 1:(n-1) loop
  for i in (k+1):n loop
    factor := a[i,k] / a[k,k];
    for j in (k+1):n loop
      a[i,j] := a[i,j] - (factor * a[k,j]);
    end for;
    b[i] := b[i] - (factor * b[k]);
  end for;
end for;
// Back Substitution
x[n] := b[n] / a[n,n];
for i in (n-1):(-1) loop
  sum := b[i];
  for j in (i+1):n loop
    sum := sum - (a[i,j] * x[j]);
  end for;
  x[i] := sum / a[i,i];
end for;

end NaiveGauss;
Hikaru 9.5-1.png

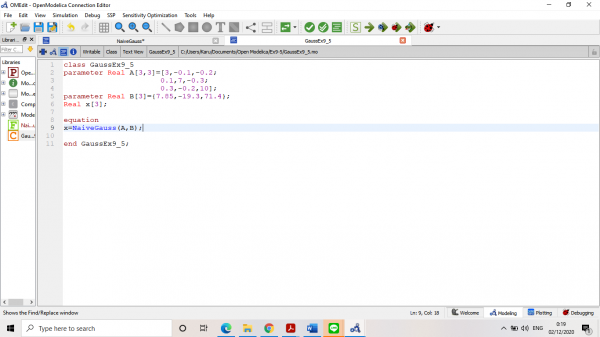
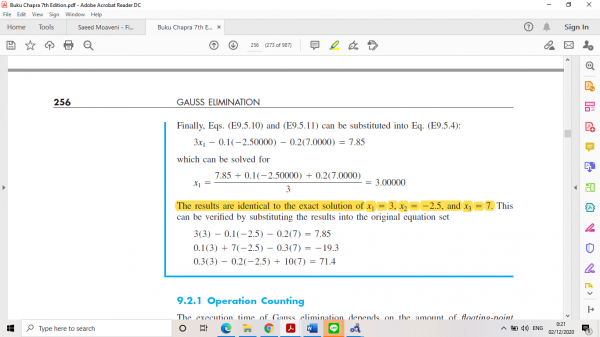
Function Naïve Gauss yang sudah dibuat tersebut dibuktikan dengan menyelesaikan example 9.5 pada buku Chapra:

Hikaru 9.5-3.png
Hikaru 9.5-2.png

Setelah code tidak mengalami error, dilakukan simulate dan didapatkan hasil yang sama dengan pembahasan pada buku:

9.5-4.png
9.5-5.png

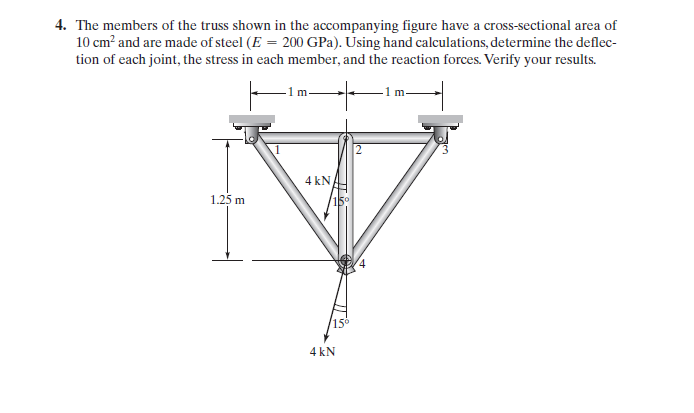
Tugas 3

Sebagai tugas 3 kami diminta menyelesaikan permalasahan truss berikut:

Pr3-1.png
Retrieved from "http://air.eng.ui.ac.id/index.php?title=Hikaru_Trinita_Salsabila&oldid=44891"