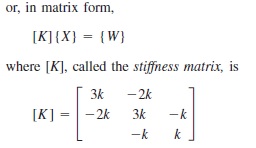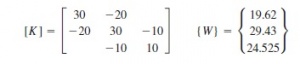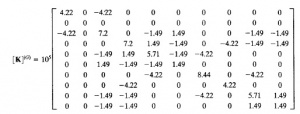Difference between revisions of "Metnum03-Christian Emanuel Kefi"
| Line 164: | Line 164: | ||
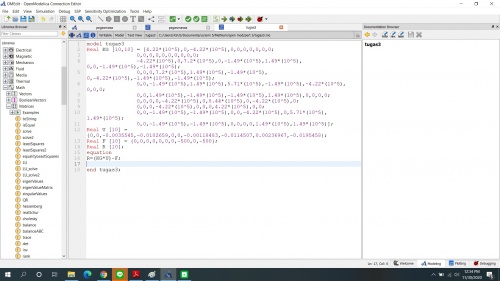
Langkah-langkah quis no.4 | Langkah-langkah quis no.4 | ||
| − | [[File:quis4.1.jpg|thumb|centre| | + | [[File:quis4.1.jpg|thumb|centre|450px]] |
| − | [[File:quis4.2.jpg|thumb|centre| | + | [[File:quis4.2.jpg|thumb|centre|450px]] |
| − | [[File:quis4.3.jpg|thumb|centre| | + | [[File:quis4.3.jpg|thumb|centre|250px]] |
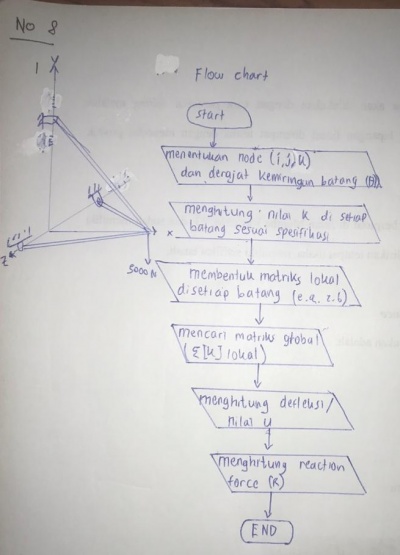
Langkah-langkah quis no.8 | Langkah-langkah quis no.8 | ||
| − | [[File:quis8.jpg|thumb|centre| | + | [[File:quis8.jpg|thumb|centre|400px]] |
Revision as of 17:47, 30 November 2020
Contents
- 1 BIODATA DIRI
- 2 Pertemuan Metode Numerik-03
- 3 Pertemuan 1 : Senin,9 November 2020
- 4 Tugas 1 : Muller's method menggunakan Openmodelica
- 5 Pertemuan 2 : Senin,16 November 2020
- 6 Tugas 2 : Class type function - untuk menyelesaikan persamaan aljabar simultan
- 7 Pertemuan 3 : Senin,23 November 2020
- 8 Tugas 3 : Beam
- 9 QUIZ Metnum 1
BIODATA DIRI
Nama : Christian Emanuel Kefi
NPM : 1906435460
Pendidikan Terakhir : Diploma III
Pertemuan Metode Numerik-03
Pertemuan 1 : Senin,9 November 2020
Pada pertemuan kali ini mereview pembelajaran sebelum UTS dan meberikan 4 indikator dalam pembelajaran yang pertama mengetahui apa yang dipelajari, yang kedua paham konsep pembelajaran yang sudah dipelajari atau diketahui tersebut, ketiga pengaplikasian dari suatu materi/konsep yang sudah dipelajari, keempat mengenali diri/ menilai diri sendiri dalam pengaplikasian yang sudah dipelajari.
Selain itu pertemuan ini disertai pemberian tugas untuk mencoba membuat program pada aplikasi openmodelica. link dibawah menghubungkan dengan video tugas tersebut.
Tugas 1 : Muller's method menggunakan Openmodelica
https://www.youtube.com/watch?v=tKEca_-MpMI
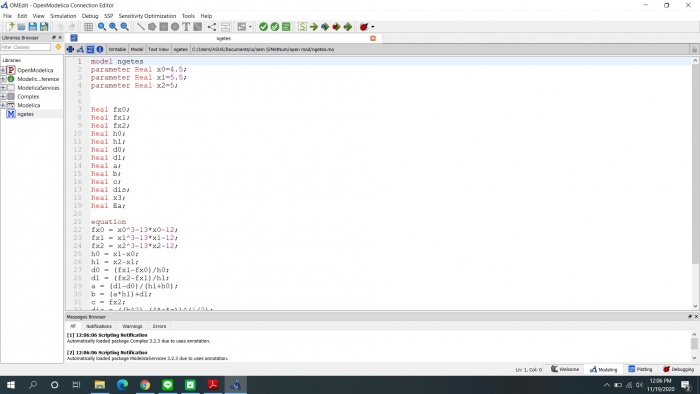
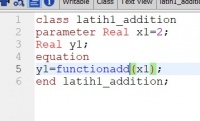
Dalam metode ini menggunakan 3 titik tebakan yang nantinya akan dimasukan kedalam persamaan kuadrat untuk mendapatkan hasil yaitu sebuah titik potong dari sebuah garis polinomial dan garis sumbu-x. Titik tersebut merupakan pendekatan untuk menemukan akar-akar dari suatu polinomial. semakin banyak iterasi yang dilakukan semakin dekat hasil perhitungan yang dilakukan dengan akar yang sebenarnya. Gambar berikut menunjukan contoh dari program perhitungan yang menjawab suatu persoalan menemukan akar-akar dari suatu polinommial :
Parameter digambar itu merupakan nilai yang diketahui atau yang nantinya akan diinput, dan nilai real adalah nilai yang ada dalam perhitungan baik yang diketahui maupun yang akan dicari.
Pertemuan 2 : Senin,16 November 2020
Pada pertemuan kali ini dilakukan penilaian terhadap PR pertama, yaitu mempelajari aplikasi openmodelica. Dari tugas tersebut saya membahas tentang Muller methods seperti yang tertera diatas.
1) Dalam pertemuan ini juga diberikan tugas membuat permodelan sederhana yaitu menjumlahkan angka 10 terhadap suatu variabel.
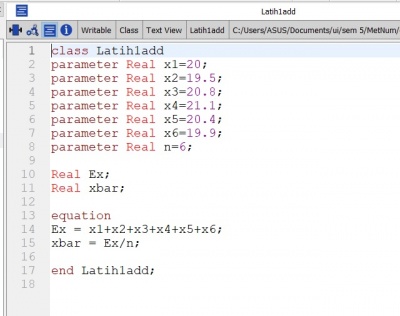
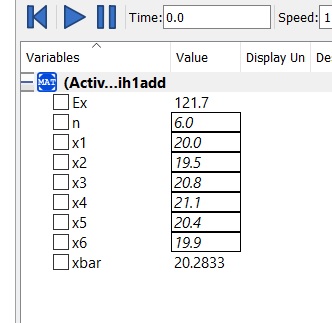
2) Selain itu juga membuat persamaan untuk mencari nilai rata-rata dari suatu data tertentu.
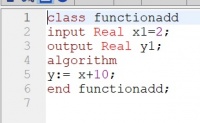
3) Selanjutnya dilakukan percobaan menbuat function class dari class pada no.1. contohnya sebagai berikut :
Tugas 2 : Class type function - untuk menyelesaikan persamaan aljabar simultan
Persamaan aljabar simultan adalah persamaan aljabar yang mempunyai lebih dari satu persamaan dan diselesaikan secara simultan. Pada umumnya, jenis persamaan aljabar simultan dapat diselesaikan dengan metode grafik, metode subtitusi, metode eliminasi gauss, dan metode cramer.
Pada percobaan pertama menggunakan metode class function pada open modelica dengan contoh soal sebagai berikut :
x1 + 2.x3 = 6
-3.x1 + 4.x2 + 6.x3 = 30
-x1 - 2.x2 + 3.x3 = 8
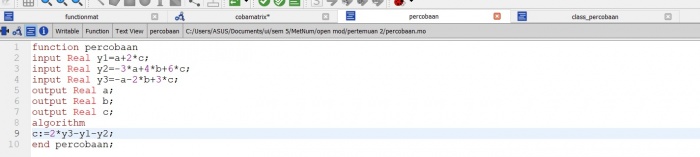
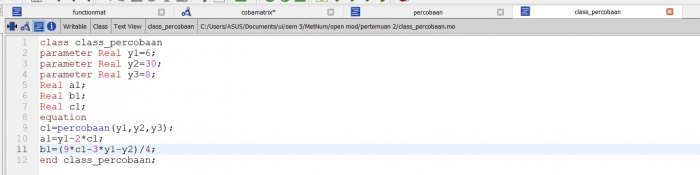
dengan contoh program function dan class sebagai berikut :
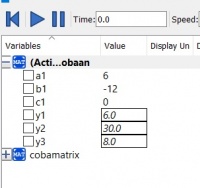
Dan hasil percobaan sebagai berikut
Pertemuan 3 : Senin,23 November 2020
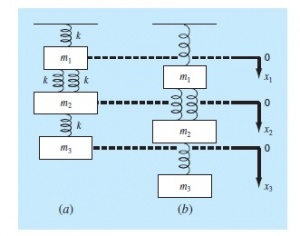
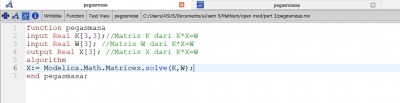
Pada pertemuan ketiga ini dijelaskan tentang masalah teknik berupa sistem pegas-masa yang terdapat pada contoh 12.11 pada buku metode numerik.
spring mass system dapat diselesaikan dengan menggunakan persamaan dari hukum Hooke. dimana variable yang digunakan sebagai berikut :
m = massa benda (kg)
k = konstanta pegas
x = Jarak perpindahan (m)
Fd-Fu = force up dan force down = merupakan force balance (zigma F)
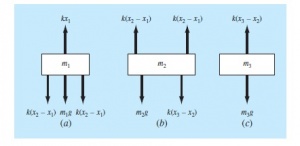
Dari gambar diatas dapat disimpulkan gaya yang bekerja pada setiap komponen diatas adalah :
1) Benda 1
kx1 = 2k(x2-x1) + m1g ----> 3kx1-2kx2=m1g
2) Benda 2
2k(x2-x1)=m2g+k(x3-x2)) -----> -2kx1 + 3kx2 - kx3 = m2g
3) Benda 3
k(x3-x2) = m3g
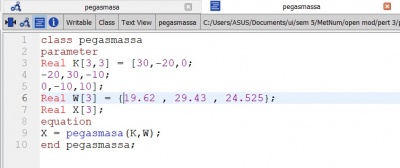
Untuk mencari nilai dari x digunakan persamaan sebagai berikut:
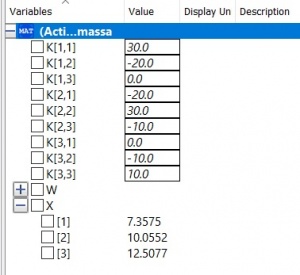
Dengan persamaan tersebut dimasukan nilai k=10 kg/s^2, dan m1 = 2 kg, m2 = 3 kg, dan m3 = 2,5 kg didapatkan hasil sebagai berikut :
Dengan menggunakan aplikasi open modelica didapatkan nilai dari x1, x2, x3 dengan langkah-langkah sebagai berikut :
Tugas 3 : Beam
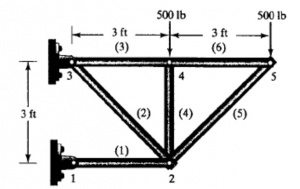
Pada tugas kali ini mencari gaya reaksi dan defleksi pada setiap titik dari beam dibawah gaya tekan seperti dibawah ini :
Semua kerangka beam terbuat dari kayu yang memiliki modulus elastisitas E = 1,9 x 10^6 lb/in dan A = 8 in^2
untuk mencari defleksi dan gaya reaksi hal yang dilakukan adalah :
1) Melakukan analisis node i, j, dan sudut dari setiap element
2) Mencari nilai kekakuan dari setiap element
- Elemen 1,3,4,6 memiliki kekakuan yang sama karena memiliki A, E, dan L yang sama
- Elemen 2, dan 5 memiliki kekakuan yang sama
3) membuat persamaan elemen-elemen
4) Dari no 3 didapatkan matriks dari individual elemen matrix, pada tahap ini dilakukan penggabungan terhadap semua individual elemen matrix
dan disederhanakan menjadi sebagai berikut :
5) Dari data yang didapatkan dari buku didapatkan matriks 10 x 10 :
karena nilai dari U1x, U1y, U3x, dan U3y = 0 , maka matriks dapat disederhanakan menjadi bentuk 6 x 6
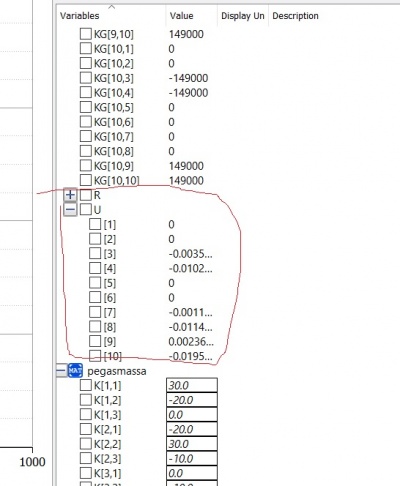
Apabila dikerjakan dengan matrix pada open modelica hasilnya sebagai berikut :
QUIZ Metnum 1
Langkah-langkah quis no.4
Langkah-langkah quis no.8