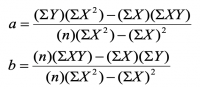Metnum03-Muhammad Bagus Pratama

بِسْمِ اللّهِ الرَّحْمَنِ الرَّحِيْ

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

BIODATA DIRI

Nama : Muhammad Bagus Pratama

NPM : 1806181792

Fakultas/ Jurusan : Teknik/ Teknik Mesin

Tempat dan Tanggal lahir :Sukabumi, 23 Augustus 2000

Pertemuan 1: 9 November 2020

Assalamualaikum Wr. Wb, Perkenalkan nama saya Muhammad Bagus Pratama dari kelas Metode Numerik 03,kali ini daya akan menjelaskan apa yang sudah saya pelajari tentang Metode Numerik. Metode numerik merupakan teknik penyelesaian permsalahn yang diformulasikan secara matematis dengan menggunakan operasi hitungan (aritmatik) yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan matematis tidak dapat diselesaikan menggunakan metode analitik. Jikapun terdapat penyelesaiannya secara analitik, proses penyelesaiaannya sering kali cukup rumit dan memakan banyak waktu sehingga tidak efisien.

Terdapat keuntungan dan kerugian terkait penggunaan metode numerik. Keuntungan dari metode ini antara lain:

1. Solusi persoalan selalu dapat diperoleh.

2. Dengan bantuan komputer, perhitungan dapat dilakukan dengan cepat serta hasil yang diperoleh dapat dibuat sedekat mungkin dengan nilai sesungguhnya.

3. Tampilan hasil perhitungan dapat disimulasikan.

Adapun kelemahan metode ini antara lain:

1. Nilai yang diperoleh berupa pendekatan atau hampiran.

2. Tanpa bantuan komputer, proses perhitungan akan berlangsung lama dan berulang-ulang.

1. Menentukan Akar-Akar

Ada beberapa metode yang dapat digunakan untuk menyelesaikan suatu persamaan. Metode ini merupakan penyelesaian perkiraan, tetapi lebih sistematis untuk menghitung akar-akar persamaan. Dalam metode numerik, pencarian akar f(x)=0 dilakukan secara lelaran (iteratif). Secara umum, semua metode pencarian akar dapat dikelompokkan menjadi 2 golongan besar :

• Metode Tertutup

Metode yang termasuk ke dalam golongan ini mencari akar di dalam selang [a,b]. Selang [a,b] sudah dipastikan berisi minimal satu buah akar, karena itu metode jenis ini selalu berhasil menemukan akar. Dengan kata lain, lelarannya selalu konvergen (menuju) ke akar, karena itu metode tertutup kadang-kadang dinamakan juga metode konvergen.

Metode yang termasuk dalam golongan ini antara lain :

a. Metode Biseksi atau Metode Setengah Interval ini merupakan Metode dengan bentuk paling sederhana diantara beberapa metode yang akan dipelajari.

b. Metode Regula Falsi atau Metode Interpolasi Linier adalah metode mudah tapi tidak efisien. Untuk mendapatkan hasil yang mendekati nilai eksak diperlukan langkah iterasi yang cukup panjang. Metode Regula Falsi dapat menutup kekurangan itu. Metode Regula Falsi didasarkan pada interpolasi antara dua nilai dari fungsi yang mempunyai tanda berlawanan

• Metode Terbuka

Yang diperlukan pada metode ini, adalah tebakan awal akar, lalu dengan prosedur lelaran, kita menggunakannya untuk menghitung hampiran akar yang baru. Pada setiap lelaran, hampiran akar lama yang dipakai untuk menghitung hampiran akar yang baru. Mungkin saja hampiran akar yang baru mendekati akar sejati (konvergen), atau mungkin menjauhinya (divergen). Karena itu, metode terbuka tidak selalu berhasil menemukan akar, kadang-kadang konvergen, kadangkala ia divergen.

Metode yang termasuk dalam golongan ini antara lain :

a. Metode Newton Raphson,Metode ini paling banyak digunakan dalam mencari akar-akar dari suatu persamaan.

b. Metode Secant,Kekurangan Metode Newton Raphson adalah diperlukannya turunan pertama (differensial) dari f(x) dalam hitungan. Kadang-kadang sulit untuk mendiferensialkan persamaan yang diselesaikan. Untuk itu maka bentuk diferensial didekati dengan nilai perkiraan berdasarkan diferensial beda hingga.

c. Metode Iterasi,Dalam metode iterasi ini digunakan suatu persamaan untuk memperkirakan nilai akar persamaan. Persamaan tersebut dikembangkan dari fungsi f(x) = 0 sehingga parameter x berada disisi kiri dari persamaan, yaitu :

X= g(x)

Persamaan ini menunjukkan bahwa nilai x merupakan fungsi dari x, sehingga dengan memberi nilai perkiraan awal dari akar dapat dihitung perkiraan baru dengan rumus iteratif berikut :

Xi+1 = g ( xi )

Besar kesalahan dihitung dengan rumus berikut :

∈a = | (Xi+1 – Xi )/(Xi+1 ) | X 100%

2. Regresi Linier

Regresi merupakan alat ukur yg digunakan untuk mengetahui ada tidaknya korelasi antarvariabel. Analisis regresi lebih akurat dlm analisis korelasi karena tingkat perubahan suatu variabel terhdp variabel lainnya dpt ditentukan). Jadi pada regresi, peramalan atau perkiraan nilai variabel terikat pada nilai variabel bebas lebih akurat pula.

Regresi linier adalah regresi yang variabel bebasnya (variabel X) berpangkat paling tinggi satu. Utk regresi sederhana, yaitu regresi linier yg hanya melibatkan dua variabel (variabel X dan Y).

Y = a + bX

Keterangan :

Y = variabel terikat

X = variabel bebas

a = intersep / konstanta

b = koefisien regresi / slop

Persamaan regresi linear di atas dpt pula dituliskan dlm bentuk :

3. Turunan Numerik

Ini digunakan untuk menentukan nilai turunan fungsi f yang diberikan dalam bentik tabel. Ada 3 pendekatan zalm menghitung Turunan Numerik :

1. Hampiran selisih-maju (forward difference approximation)

2. Hampiran selisih-mundur (backward difference approximation)

3. Hampiran selisih-pusat (central difference approximation)

Pertemuan 2: 16 November 2020

Assalamualaikum Wr Wb,pada pertemuan kedua ini, Pak Dai emulai kelas dengan pemaparan pemahaman masing-masing mengenai OpenModelica. Setelah itu kami diminta untuk membuat sebuah program sederhana untuk menjumlahkan angka dan juga mencari rata-rata.

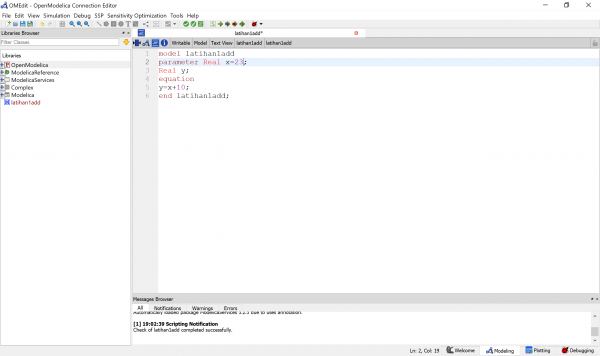
Berikut merupakan algoritma yang saya buat untuk penjumlahan angka

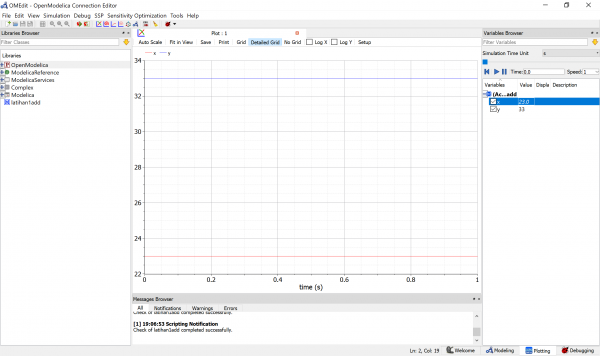
Setelah itu dapat dilihat grafik input dan hasil sebagai berikut, dengan nilai input x=6 didapatkan hasil y=16. Kita juga dapat melakukan simulasi kembali apabila ingin merubah nilai x.

Tugas 2 : Memecahkan suatu Persamaan Aljabar Simultan

Assalamualaikum Wr,Wb, Dalam menyelesaikan tugas kedua ini saya menggunakan 3 persamaan sebagai berikut :

x1+4x2+6x3=7

3x1+5x2+2x3=6

x1+3x2+2x3=4

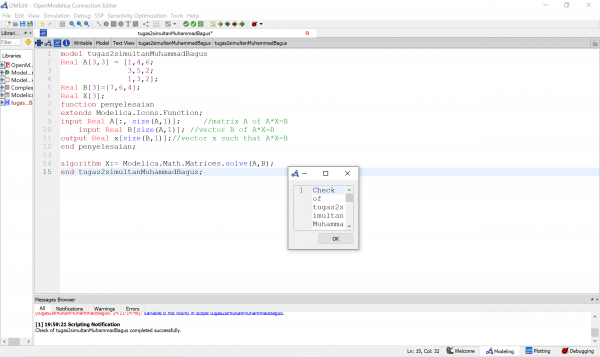
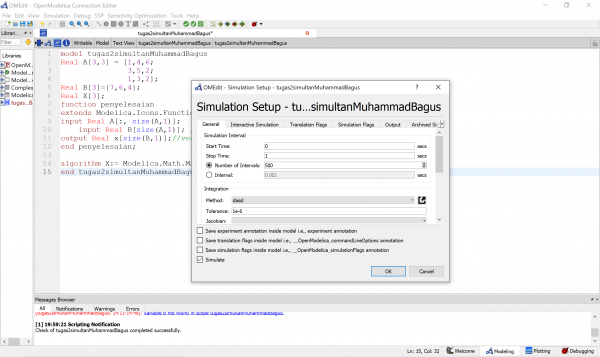
Langkah pertama yang saya lakukan adalah membuat modelica class baru dengan tipe class dan membruta fungsi dan variabel real seperti A[3,3] , B[3] dan parameter X, dimana X adalah akar yang akan ticari setelah dilakukan simulasi. Class yang saya gunakan adalah tipe class yang bisa menyelesaikan persamaan yaitu class tipe function. Berikut basil rangkaian bahasa modelica yang Sudan di cek dengan berisikan 15 persamaan dan 15 variabel yang Sudan benar :

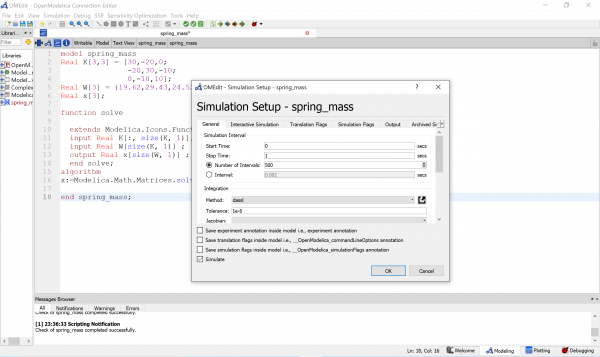
Selanjutnya saya melakukan setting simulation sebagai berikut :

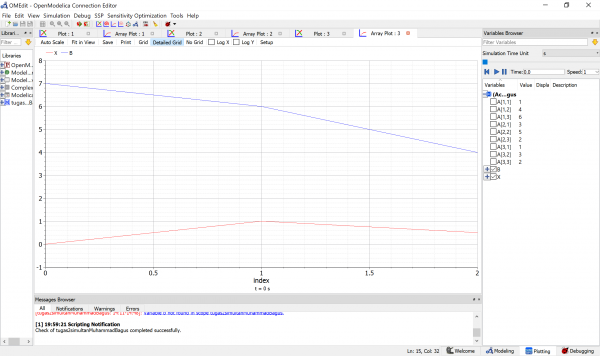
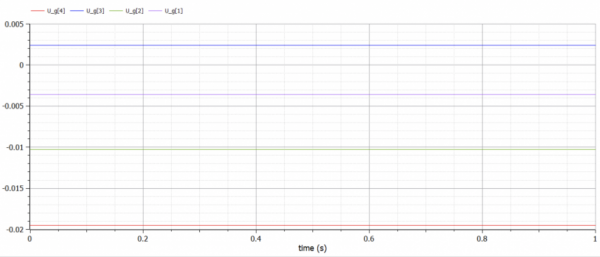
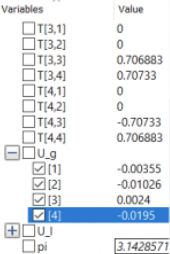
Setelah dilakukan simulasi, didapatkan akar- akar dari persamaan eliminasi gauss yaitu :

X1 = 9,25186e-16

X2 = 1

X3 = 0,5

Berikut adalah basil simulasi yang telah saya lakukan :

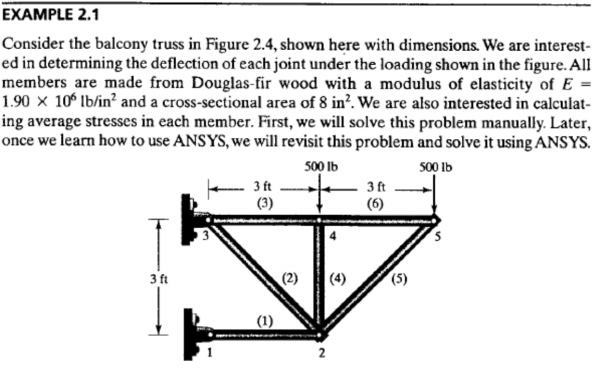
Pertemuan 3 : 23 November 2020

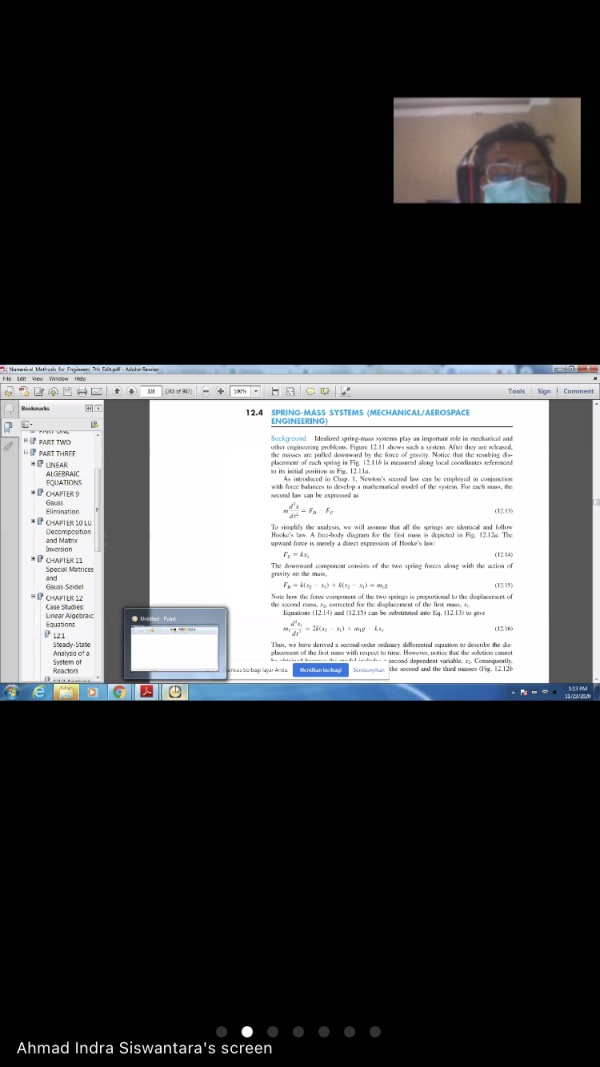
Assalamualaikum Wr.Wb, Pada hari ini kelas akan diadakan oleh Pak Dai menghimbau kami untuk membaca materi mengenai permodelan pegas di buku metode numerik terlebih dahulu.

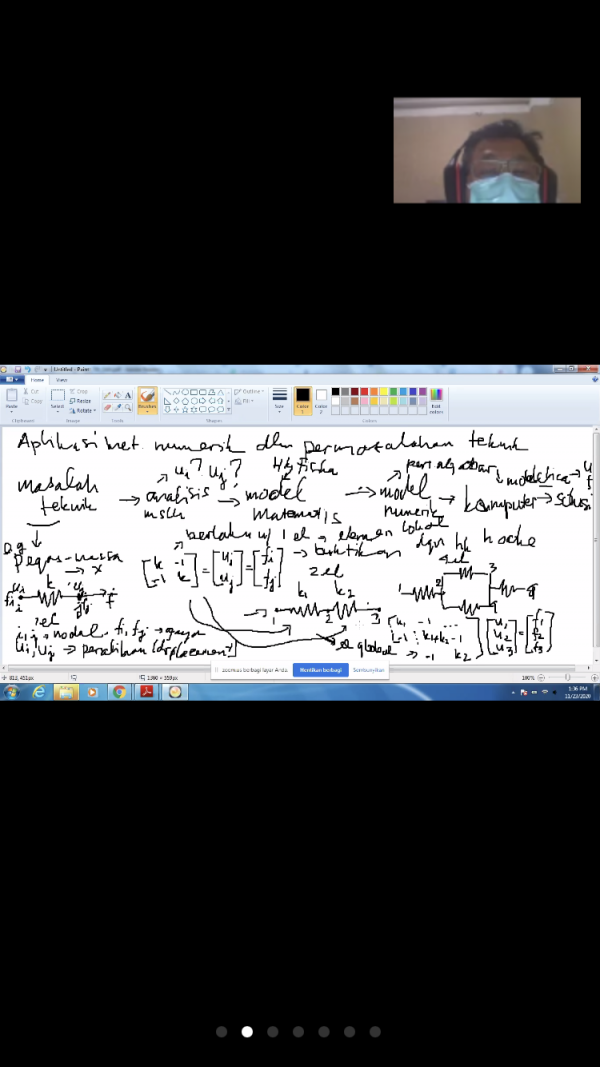
Kemudian, pak Dai menjelaskan bagaimana cara mengaplikasikan metode numerik ke permodelan teknik. Masalah teknik -> analisis teknik -> model matematis -> model numerik -> komputer -> solusi

Lalu Pak Dai menjelaskan bagaimana permodelan aplikasi pegas. Mulai dari masalah tekniknya yaitu merupakan sistem pegas. kemudian pada analisis teknik kita menentukan hal-hal apa saja yang kita ketahui dalam persamaan tersebut. Lalu dengan hukum hooke kita membuat model matematisnya.

Selanjutnya, pak Dai memberikan tugas untuk menyelesaikan permasalahan pada pegas massa, dan berikut adalah hasil dari pembuatan class yang telah dibuat : .Menggunakan matriks 3x3 sesuai permasalahan yang ada

.Mengunakan asumsi nilai k yaitu 10N/m untuk disubtitusi ke persamaan

.Menggunakan salah satu metode aljabar simultan yaitu gauss elimination

.Terdapat 15 persamaan dan 15 variabel,12 trivial equation

Kemudian Pak Dai menghimbau kami untuk membuktikan matriks sistem pegas yang ada di buku dengan perhitungan pada openmodelica.

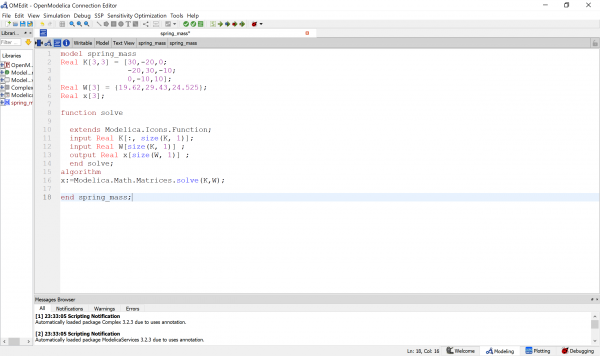
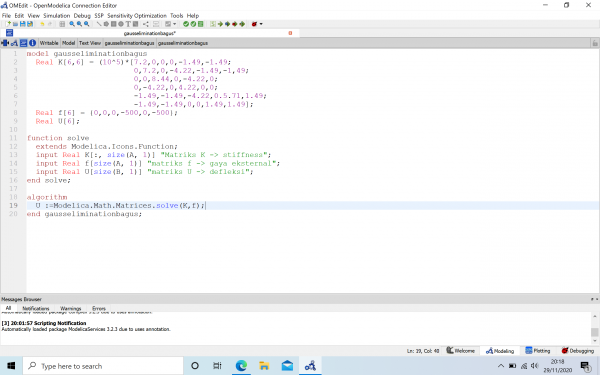
Berikut koding pada open modelica saya :

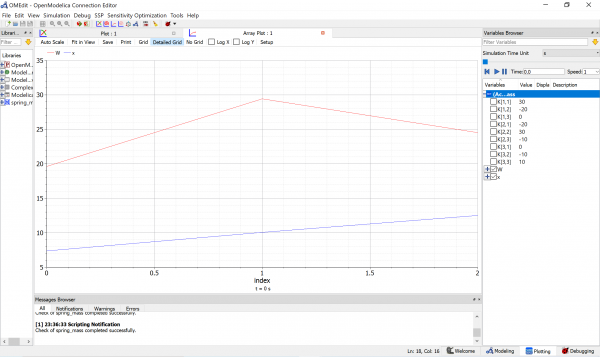
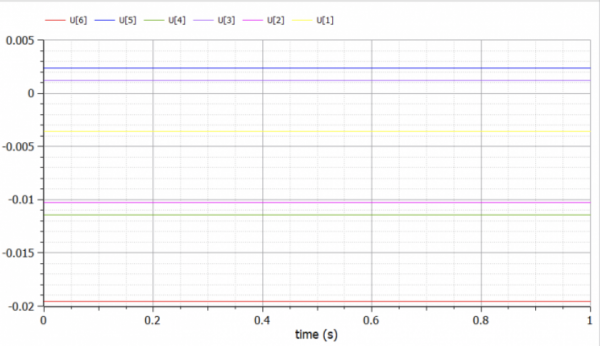
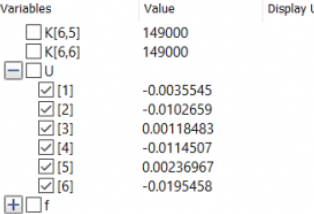
Dari basil tersebut di dapatkan x1, x2, dan x3. Berikut adalah hasilnya, dimana x1 = 7.5 N, x2 = 10.25N, dan x3 = 12.75 N.

Demikian basil Openmodelica dari saya, Terima Kasih. Wassalamualaikum Wr,Wb

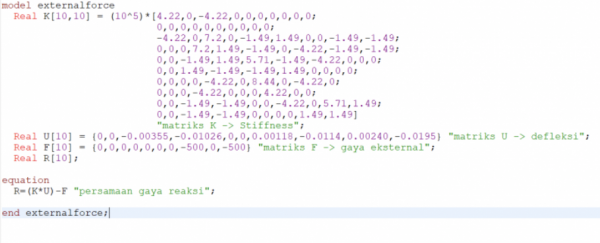
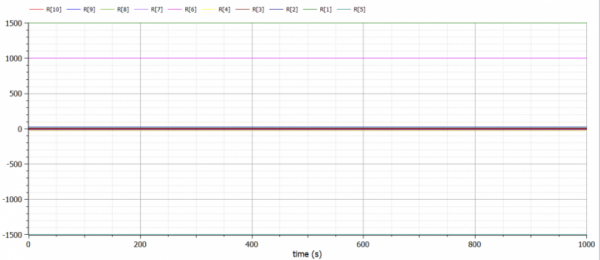
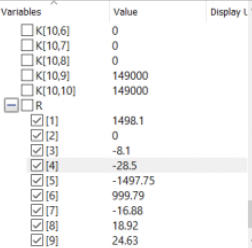
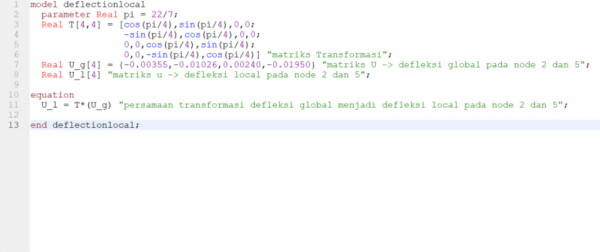
Tugas 3

Ada 3 that pertama Dalam menyelesaikan coal diatas