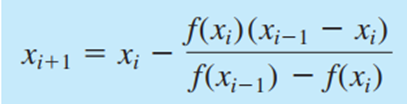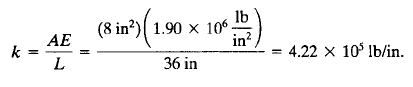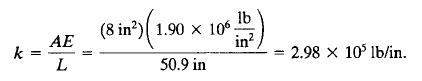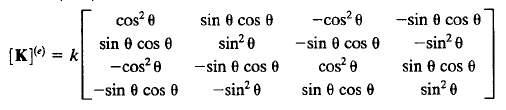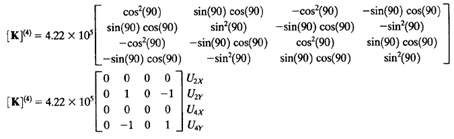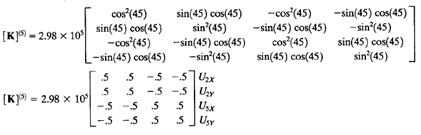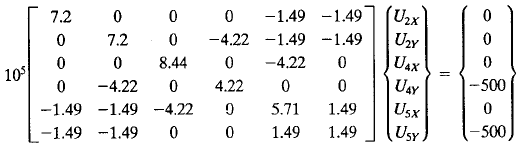Difference between revisions of "Metnum03-Dendy Dwi Rohma P J"
(→TRUSS ANALYSIS MATRIX) |
(→TRUSS ANALYSIS MATRIX) |
||
| Line 83: | Line 83: | ||
[[File:2_Truss_MenjadiNode.png]] | [[File:2_Truss_MenjadiNode.png]] | ||
| − | + | Setelah itu dilakukan perkalian untuk mencari nilai kekakuan setiap truss/ element dengan rumus k=A.E/L. Namun sebelumnya dilakukan pengelompokan berdasarkan panjang batang/truss lalu didapatkan batang dengan panjang yang sama (1,3,4,6) dan batang (2,5). Namun untuk mendapatkan nilai K lokal nilai k(kekakuan) harus terlebih dahulu dikalikan dengan rumus K lokal dalam bentuk matrix 4x4. | |
[[File:3_KonstantaStiffness_1.3.4.6.png]] | [[File:3_KonstantaStiffness_1.3.4.6.png]] | ||
[[File:3_KonstantaStiffness_2.5.png]] | [[File:3_KonstantaStiffness_2.5.png]] | ||
| + | |||
| + | Nah rumus K^e atau K lokal menurut pemahaman saya dapat berbeda-beda tergantung dengan susunan dari truss (sudut yang terbentuk dari sb. refrensi yang kita gunakan) atau batang dan tumpuan yang kita gunakan. Lalu untuk nilai k (kekakuan) hanya dipengaruhi dari cross section area (A), elastisitas (E) dan panjang batang (L) | ||
[[File:4_RumusK.png]] | [[File:4_RumusK.png]] | ||
| + | |||
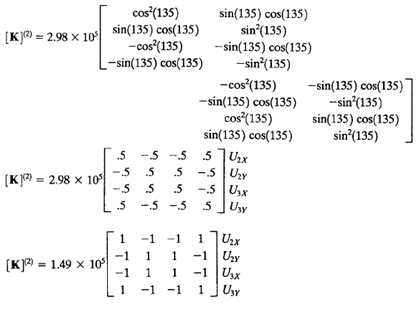
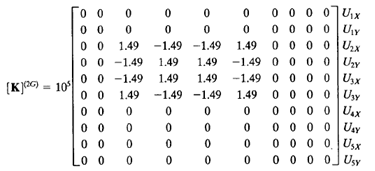
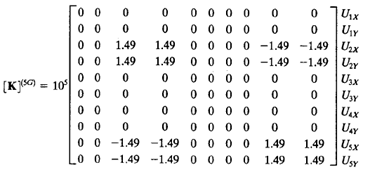
| + | Analisa batang pada contoh soal ini jg dapat dikelompokan berdasarkan panjang batangnya. Jadi untuk analisa pertama batang (1,3,4,6) dan batang (2 dan 5). Pada batang (1,3,dan 6) memiliki sudut refrensi yang sama yaitu 0 derajat, namun ketiga element ini memiliki node yang berbeda sehingga akan berpengaruh pada peletakan hasil matrix 4x4 pada matrix global (K^G) 10x10. | ||
[[File:5_1_AnalisaElemen4.png]] | [[File:5_1_AnalisaElemen4.png]] | ||
| + | |||
| + | Pada gambar dibawah ini | ||
[[File:5_2_Elemen4_DiglobalMatrik.png]] | [[File:5_2_Elemen4_DiglobalMatrik.png]] | ||
Revision as of 11:17, 30 November 2020
Assalamualaikum Warahmatullahi Wabarakatuh
Nama:Dendy Dwi Rohma P J
NPM: 1906435473
Contents
Pertemuan 1
1. Tugas_01_MetodeNumerik03
Dalam mencari nilai suatu akar dari suatu persamaan atau permasalahan yang ada, berbagai macam cara dan metode, berikut ini bermacam-macam metode yang dapat kita gunakan dalam mencari nilai suatu akar persamaan :
1. Metode Bagi dua (Bisection)
2. Metode False Position
3. Metode Secant
4. Metode Iterasi Titik Tetap
5. Metode Newton Raphson
Dalam kesempatan kali ini saya akan membahas tentang metode secant.
Pengertian Metode Secant
Metode secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimana kemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik.Tujuan dan Fungsi Tujuan metode secant adalah untuk menyelesaikan masalah yang terdapat pada metode Newton-Raphson yang terkadang sulit mendapatkan turunan pertama yaitu f'(x). Fungsi metode secant adalah untuk menaksirkan akar dengan menggunakan diferensi daripada turunan untuk memperkirakan kemiringan/slope.
Algoritma Metode Secant 1. Definisikan fungsi F(x) 2. Definisikan torelansi error (e) dan iterasi maksimum (n) 3. Masukkan dua nilai pendekatan awal yang di antaranya terdapat akar yaitu x0 dan x1,sebaiknya gunakan metode tabel atau grafis untuk menjamin titik pendakatannya adalah titik pendekatan yang konvergensinya pada akar persamaan yang diharapkan.
SOAL 1
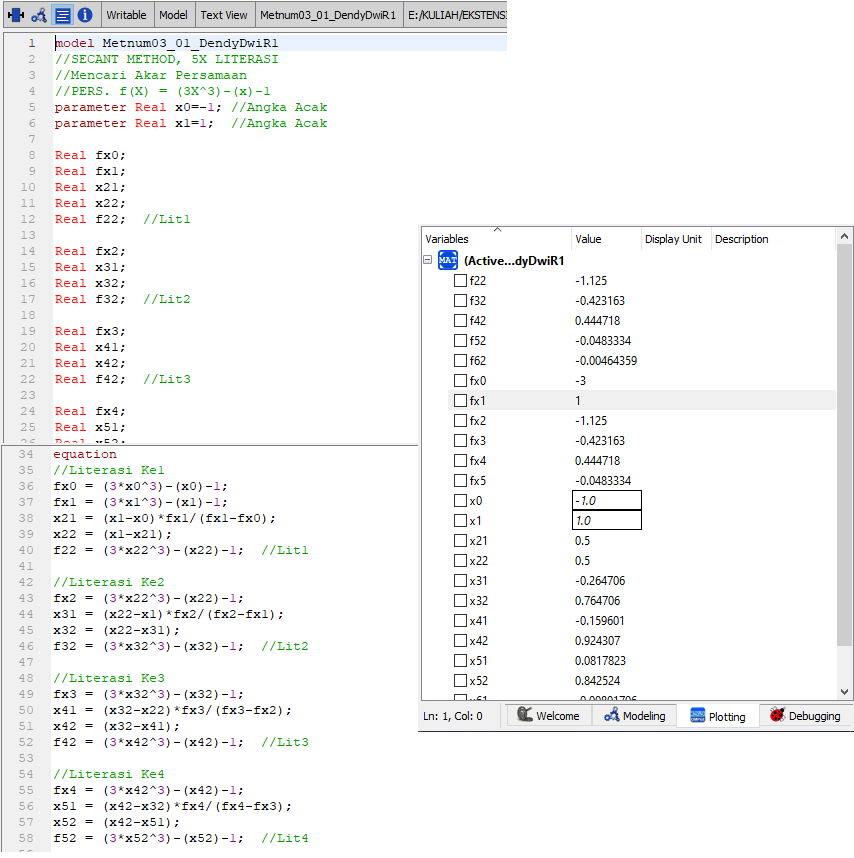
Cari Akar Persamaan dari Persamaan f(x) dengan Metode Secant Method pada Literasi ke 4? f(x) = 3x^3 -x -1
Asumsi:
x0 = -1
x = 1
Penjelasan menganai pemrograman Secant Method menggunakan OpenModelica terlampir dalam Link dibawah ini:
Link Youtube : https://www.youtube.com/watch?v=Bk_QtrInpks
Pertemuan 2
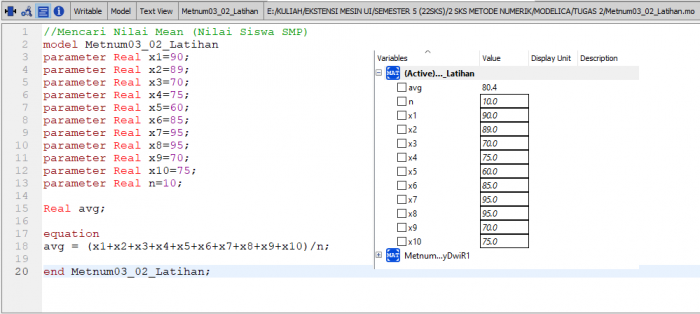
Melakukan latihan mencari nilai mean dari persamaan dan data sederhana.
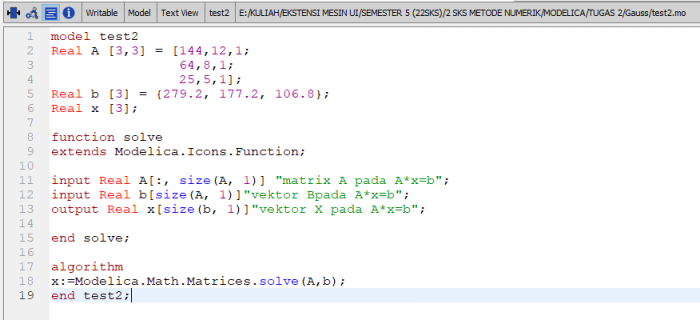
PR Eliminasi Gauss
Pertemuan 3
3. Tugas_03_MetodeNumerik03
MASS SPRING ANALYSIS MATRIX
TRUSS ANALYSIS MATRIX
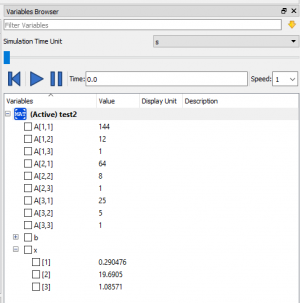
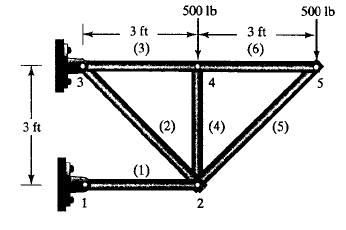
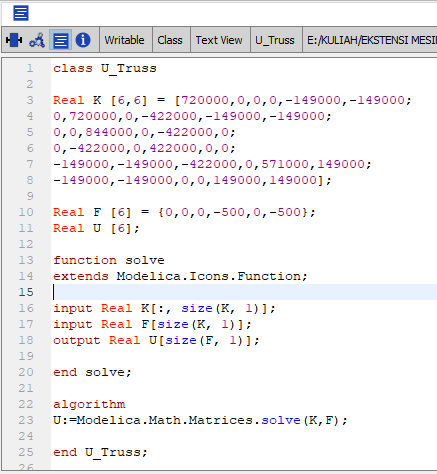
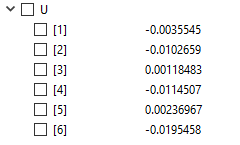
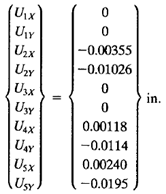
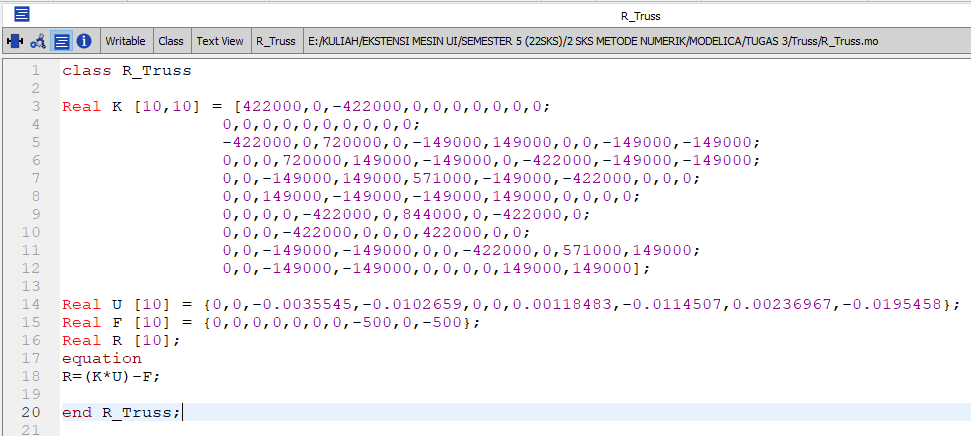
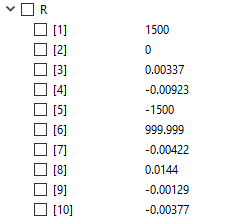
Tugas kali ini disuruh mencari nilai defleksi/dX/U pada suatu truss yang disusun dan dikenai pembebanan dan tumpuan seperti pada soal dibawah ini. Lalu kemudian setelah kita menemukan nilai U lalu digunakan untuk mencari reaksi gaya (R) pada setiap elemen truss.
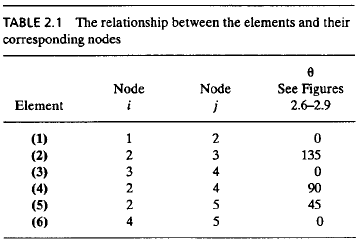
Berdasarkan susunan truss diatas, kita harus mampu menjabarkan setiap beam/ truss menjadi notasi element, tumpuan menjadi notasi node dan sudut element terhadap garis refrensi yg kita pilih (saya menggunakan X positif sbg sb.0 deg). Lalu setelah dilakukan penjabaran berdasarkan element, node dan sudut didapatkan Tabel 2.1 sebagai hubungannya.
Setelah itu dilakukan perkalian untuk mencari nilai kekakuan setiap truss/ element dengan rumus k=A.E/L. Namun sebelumnya dilakukan pengelompokan berdasarkan panjang batang/truss lalu didapatkan batang dengan panjang yang sama (1,3,4,6) dan batang (2,5). Namun untuk mendapatkan nilai K lokal nilai k(kekakuan) harus terlebih dahulu dikalikan dengan rumus K lokal dalam bentuk matrix 4x4.
Nah rumus K^e atau K lokal menurut pemahaman saya dapat berbeda-beda tergantung dengan susunan dari truss (sudut yang terbentuk dari sb. refrensi yang kita gunakan) atau batang dan tumpuan yang kita gunakan. Lalu untuk nilai k (kekakuan) hanya dipengaruhi dari cross section area (A), elastisitas (E) dan panjang batang (L)
Analisa batang pada contoh soal ini jg dapat dikelompokan berdasarkan panjang batangnya. Jadi untuk analisa pertama batang (1,3,4,6) dan batang (2 dan 5). Pada batang (1,3,dan 6) memiliki sudut refrensi yang sama yaitu 0 derajat, namun ketiga element ini memiliki node yang berbeda sehingga akan berpengaruh pada peletakan hasil matrix 4x4 pada matrix global (K^G) 10x10.
Pada gambar dibawah ini