Difference between revisions of "Metnum03-Ahmad Farras"
Ahmad Farras (talk | contribs) |
Ahmad Farras (talk | contribs) (→Tugas 3 Metode Numerik) |
||
| Line 92: | Line 92: | ||
== Tugas 3 Metode Numerik == | == Tugas 3 Metode Numerik == | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
| + | |||
Hitung defleksi yang terjadi pada tiap elemen, dan gaya reaksinya! | Hitung defleksi yang terjadi pada tiap elemen, dan gaya reaksinya! | ||
Mengubah problem menjadi node dan elemen | Mengubah problem menjadi node dan elemen | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
Asumsikan solusi yang mendekati sifat elemen | Asumsikan solusi yang mendekati sifat elemen | ||
Menentukan nilai konstanta kekakuan/stiffness constant dari elemen | Menentukan nilai konstanta kekakuan/stiffness constant dari elemen | ||
- Elemen 1,3,4,6 | - Elemen 1,3,4,6 | ||
| − | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] | |
- Elemen 2,4 | - Elemen 2,4 | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
Membuat persamaan untuk elemen | Membuat persamaan untuk elemen | ||
| Line 113: | Line 114: | ||
Lalu diaplikasikan pada elemen 1,3,6 | Lalu diaplikasikan pada elemen 1,3,6 | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
Posisi di dalam matriks global untuk elemen 1,3,6 dengan θ=0° adalah | Posisi di dalam matriks global untuk elemen 1,3,6 dengan θ=0° adalah | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
| − | |||
Analisis Elemen 4 | Analisis Elemen 4 | ||
Karena elemen 4 sejajar dengan sumbu Y global, maka θ=90° | Karena elemen 4 sejajar dengan sumbu Y global, maka θ=90° | ||
| − | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] | |
Posisi elemen 4 dalam matriks global adalah | Posisi elemen 4 dalam matriks global adalah | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
Analisis Elemen 2,5 | Analisis Elemen 2,5 | ||
Untuk elemen 2 dan 5 memiliki sudut terhadap sumbu koordinat global, θ=135° | Untuk elemen 2 dan 5 memiliki sudut terhadap sumbu koordinat global, θ=135° | ||
| − | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] | |
Posisi elemen 2 dan 5 dalam matriks global adalah | Posisi elemen 2 dan 5 dalam matriks global adalah | ||
| − | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] | |
Menyusun dan menggabungkan matriks elemen-elemen | Menyusun dan menggabungkan matriks elemen-elemen | ||
| − | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] | |
Menerapkan kondisi batas dan beban | Menerapkan kondisi batas dan beban | ||
Pada kasus ini, kondisi batas untuk node 1 dan 3 adalah fixed maka untuk Ux1 Ux3 Uy1 Uy3 adalah 0 diakrenakan tidak ada defleksi yang terjadi pada kasus berikut, sehingga | Pada kasus ini, kondisi batas untuk node 1 dan 3 adalah fixed maka untuk Ux1 Ux3 Uy1 Uy3 adalah 0 diakrenakan tidak ada defleksi yang terjadi pada kasus berikut, sehingga | ||
Kondisi diatas menyatakan bahwa beban eksternal diberikan pada node 4 dan 5, sehingga | Kondisi diatas menyatakan bahwa beban eksternal diberikan pada node 4 dan 5, sehingga | ||
| − | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] | |
Dengan menerapkan Hukum Hooke F= k.x, maka dalam persamaan matrix menjadi [F]=[K(G)][U¬(e)], sehingga didapatkan: | Dengan menerapkan Hukum Hooke F= k.x, maka dalam persamaan matrix menjadi [F]=[K(G)][U¬(e)], sehingga didapatkan: | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
Karena , maka kita dapat mengeliminasi baris dan kolom 1, 2, 5, 6 untuk menyederhanakan matriks. Setelah menyederhanakan matriks, didapatkan matriks 6 x 6 yaitu | Karena , maka kita dapat mengeliminasi baris dan kolom 1, 2, 5, 6 untuk menyederhanakan matriks. Setelah menyederhanakan matriks, didapatkan matriks 6 x 6 yaitu | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
pada hasil diatas saya menggunakan openmodelica untuk mendapatkan hasil defleksi pada kolom 1,2,5,6 yang programnya sebagai berikut | pada hasil diatas saya menggunakan openmodelica untuk mendapatkan hasil defleksi pada kolom 1,2,5,6 yang programnya sebagai berikut | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
Setelah menggunakan modelica untuk mencari solusi, U,yaitu defleksi elemen yang ditinjau dari koordinat global didapatkan nilai sebagai berikut | Setelah menggunakan modelica untuk mencari solusi, U,yaitu defleksi elemen yang ditinjau dari koordinat global didapatkan nilai sebagai berikut | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
| Line 161: | Line 161: | ||
Dengan menerapkan Matriks yang kita ketahui [K], {U} dan {F}, maka didapatkan | Dengan menerapkan Matriks yang kita ketahui [K], {U} dan {F}, maka didapatkan | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
Pada permasalahan ini saya mencoba program dengan openmodelica berikut program yang saya buat. | Pada permasalahan ini saya mencoba program dengan openmodelica berikut program yang saya buat. | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
Pada kasus ini jika kita memasukkan angka yang sudah dibulatkan pada buku akan menghasilkan angka sebagai berikut | Pada kasus ini jika kita memasukkan angka yang sudah dibulatkan pada buku akan menghasilkan angka sebagai berikut | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
Jika kita menggunakan angka yang kita dapat pada program defleksi maka angkanya akan sebagai berikut: | Jika kita menggunakan angka yang kita dapat pada program defleksi maka angkanya akan sebagai berikut: | ||
| − | [[File: | + | [[File:Openmodelicaahmadfarras30.JPG|centre|500px|center]] |
jadi dapat disimpulkan pembulatan pada metode numerik lebih baik dihindarkan untuk mendapatkan hasil yang lebih akurat | jadi dapat disimpulkan pembulatan pada metode numerik lebih baik dihindarkan untuk mendapatkan hasil yang lebih akurat | ||
Revision as of 10:09, 30 November 2020
Assalamualaikum wrwb
Nama Ahmad Farras NPM 1906435435
Contents
Pertemuan pertama 9 November 2020
Disini Bapak Indra memberi tugas untuk membuat open modelica dengan materi yang sudah dipelajari sebelum UTS Berikut video yang terkait yang telah saya buat
https://www.youtube.com/watch?v=XSdRoteD3d4
Pertemuan Kedua 16 November 2020
Pada pertemua ini Bapak Indra memberi tugas untuk membuat suatu program sederhana yang dimana program tersebut di koding pada openmodelica,Berikut ialah penjelasan menggunakan openmodelica untuk mencari mean pada suatu data:
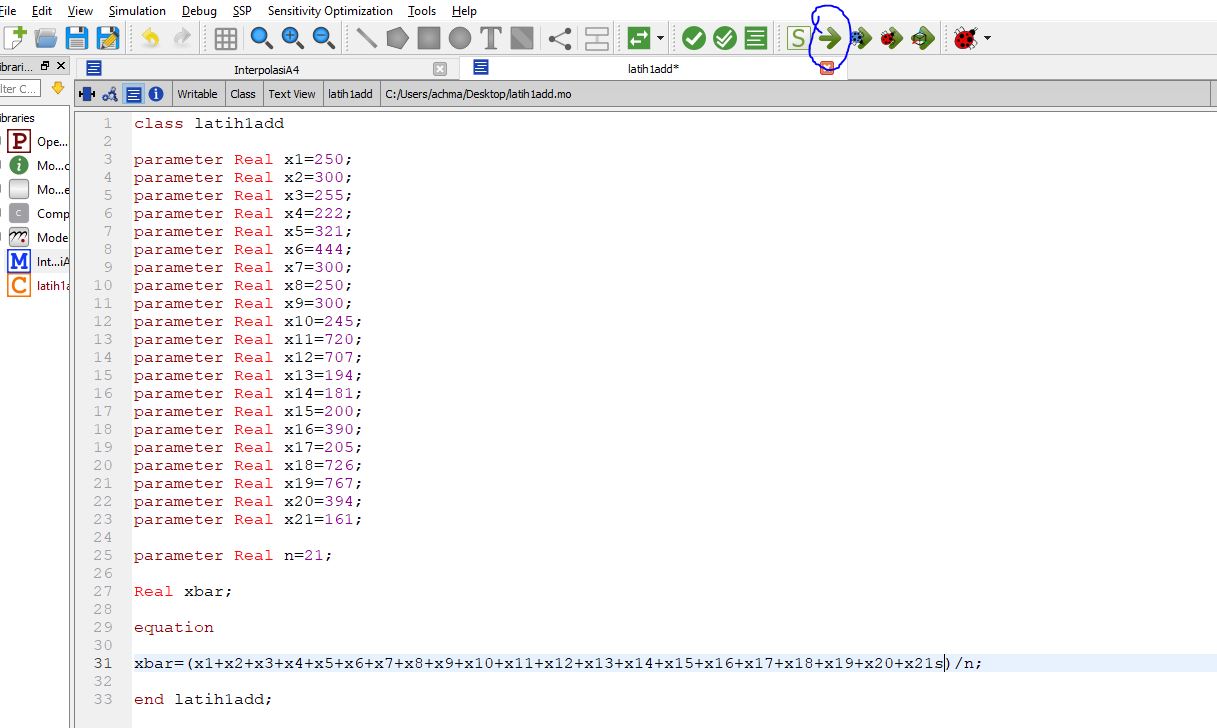
1.Menginput data,nilai yang dicari dan equation yang digunakan
Disini kita menginput data data yang dibutuhkan pada persoalan ini saya mengambil sampel 21 data.Hal tersebut kita masukan ke parameter real seperti gambar diatas.Parameter real digunakan untuk memberi informasi data yang diketahui.Setelah itu menulis "real" untuk angka yang dicari.Setelah data yang diketahui dan ditanyakan sudah dilakukan maka kita langsung menulis equation yang dimana equation pada data ini ialah
xbar=(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17+x18+x19+x20+x21)/n;
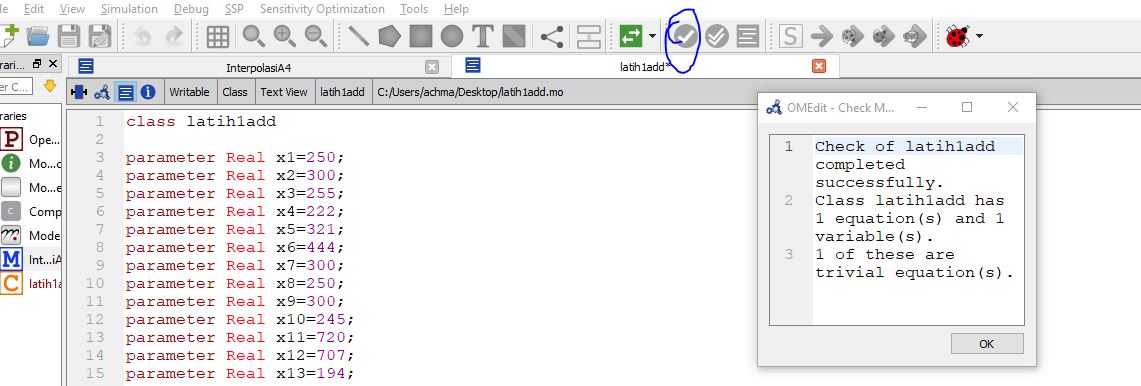
2.Mengecek dari program yang kita buat
Pada step ini kita mengecek apakah program kita apakah sudah bisa disimulasi atau tidak bisa disimulasi
3.Jika bisa maka langsung mengeklik tombol "simulate"
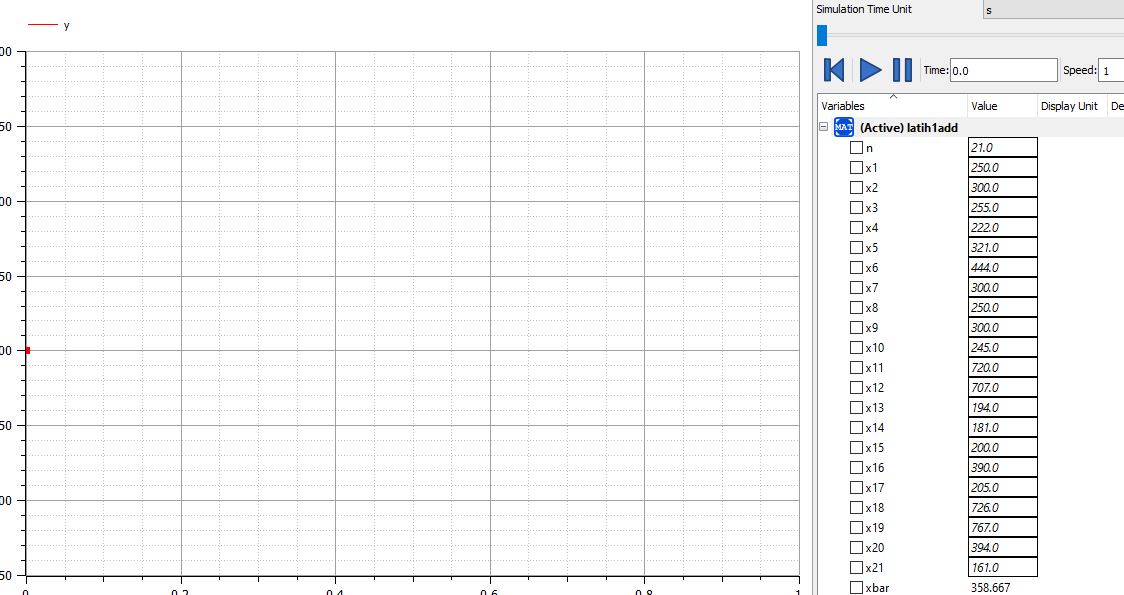
4.Berikut hasil dari nilai rata rata dari data yang saya buat
Tugas 2
Persamaan aljabar simultan tersebut dapat diselesaikan dengan matematik secara umum seperti Gauss Elimination, atau menggunakan metode lain seperti Gauss Elimination yang melibatkan matriks,atau Gauss Seidel.Pada persoalan dibawah ini saya akan menggunakan metode Gauss Elimination untuk menyelesaikan persamaan berikut.
10x1 - x2 +2x3=6
-x1+11x2-x3+3x4=25
2x1-x2+10x3-x4=-11
3x2-x3+8x4=15
Gauss Elimination adalah algoritme yang digunakan untuk menyelesaikan persamaan linear. Metode ini melibatkan perubahan bentuk sistem persamaan menjadi bentuk matriks. Setelah mengubah sistem dalam bentuk matriks,dilakukan pengurangan baris dengan mengganti posisi baris, dan/atau melakukan operasi penjumlahan dan pengurangan antar baris.
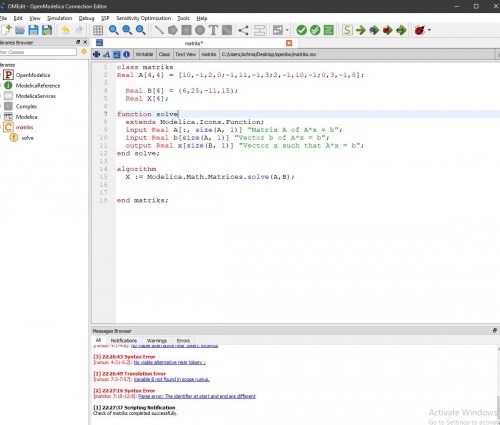
Pada aplikasi OpenModelica terdapat model untuk menyelesaikan permasalahan aljabar simultan dengan menggunakan metode Gauss Elimination.Berikut ialah model yang saya buat dengan software OpenModelica:
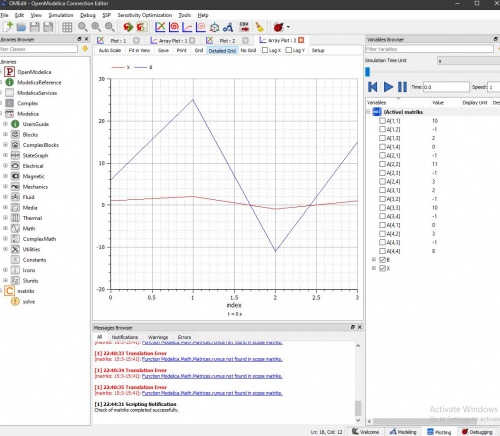
Saya menggunakan perintah yang ada di library modelica yaitu "Modelica.Math.Matrices.solve(A,b)" untuk menyelesaikan sistem persamaan linier eliminasi gauss yang ada diatas.Setelah melakukan pengecekan dan melakukan simulasi terhadap model yang telah saya buat,selanjutnya melakukan plotting terhadap hasil simulasi tersebut. Berikut adalah hasil plotting dari simulasi persamaan diatas:
hasil X yang dihasilkan dari penyelesaian persamaan diatas ialah (1,-2,1,1)
Pertemuan ketiga 23 November 2020
Pada perkuliahan ini Pak dai meyuruh kita mencoba untuk menghitung sistem spring berikut
Untuk penjabaran gaya-gaya yang bekerja pada masing-masing massa adalah sebagai berikut
Selanjutnya untuk massa 1=
1.) Subjek Massa 1
2K(x2-x1)-Kx1+m1g= m d^2 x1/dt^2 dikarenakan tidak adanya percepatan pada sistem maka m d^2 x1/dt^2 =0
3kx1 - 2kx2=m1g ......(1)
2.) Subjek Massa 2
k(x3-x2) - (2k(x2-x1))+m2g=0
-kx3 + 3kx2-2kx1=m2g ......(2)
3.) Subjek Massa 3
-k(x3-x2) +m3g=0
-kx2 + kx3=m3g .......(3)
Tugas 3 Metode Numerik
Hitung defleksi yang terjadi pada tiap elemen, dan gaya reaksinya!
Mengubah problem menjadi node dan elemen
Asumsikan solusi yang mendekati sifat elemen Menentukan nilai konstanta kekakuan/stiffness constant dari elemen - Elemen 1,3,4,6
- Elemen 2,4
Membuat persamaan untuk elemen Analisis Elemen 1,3,6 Karena orientasi elemen 1,3,6 searah dengan sumbu X global, maka koordinat local sejajar dengan koordinat global Sehingga persamaan matrix umum untuk kekakuan batangnya adalah
[K] adalah matrix untuk kekakuan k, dan (e) adalah elemen yang akan dianalisa
Lalu diaplikasikan pada elemen 1,3,6
Posisi di dalam matriks global untuk elemen 1,3,6 dengan θ=0° adalah
Analisis Elemen 4 Karena elemen 4 sejajar dengan sumbu Y global, maka θ=90°
Posisi elemen 4 dalam matriks global adalah
Analisis Elemen 2,5 Untuk elemen 2 dan 5 memiliki sudut terhadap sumbu koordinat global, θ=135°
Posisi elemen 2 dan 5 dalam matriks global adalah
Menyusun dan menggabungkan matriks elemen-elemen
Menerapkan kondisi batas dan beban Pada kasus ini, kondisi batas untuk node 1 dan 3 adalah fixed maka untuk Ux1 Ux3 Uy1 Uy3 adalah 0 diakrenakan tidak ada defleksi yang terjadi pada kasus berikut, sehingga Kondisi diatas menyatakan bahwa beban eksternal diberikan pada node 4 dan 5, sehingga
Dengan menerapkan Hukum Hooke F= k.x, maka dalam persamaan matrix menjadi [F]=[K(G)][U¬(e)], sehingga didapatkan:
Karena , maka kita dapat mengeliminasi baris dan kolom 1, 2, 5, 6 untuk menyederhanakan matriks. Setelah menyederhanakan matriks, didapatkan matriks 6 x 6 yaitu
pada hasil diatas saya menggunakan openmodelica untuk mendapatkan hasil defleksi pada kolom 1,2,5,6 yang programnya sebagai berikut
Setelah menggunakan modelica untuk mencari solusi, U,yaitu defleksi elemen yang ditinjau dari koordinat global didapatkan nilai sebagai berikut
Perlu diingat bahwa defleksi ini ditinjau dari koordinat global
Mendapatkan nilai Gaya Reaksi kita dapat menggunakan metode berikut:
Karena pada soal ingin mencari gaya reaksi, maka perlu dilakukan perhitungan pada gaya reaksi dengan persamaan
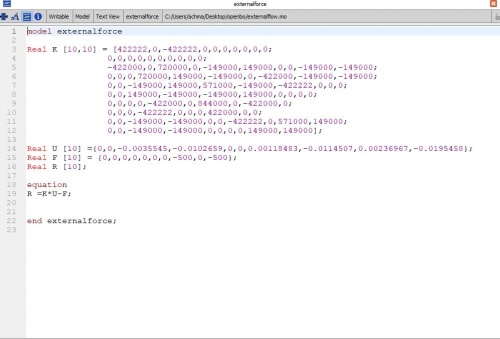
Dengan menerapkan Matriks yang kita ketahui [K], {U} dan {F}, maka didapatkan
Pada permasalahan ini saya mencoba program dengan openmodelica berikut program yang saya buat.
Pada kasus ini jika kita memasukkan angka yang sudah dibulatkan pada buku akan menghasilkan angka sebagai berikut
Jika kita menggunakan angka yang kita dapat pada program defleksi maka angkanya akan sebagai berikut:
jadi dapat disimpulkan pembulatan pada metode numerik lebih baik dihindarkan untuk mendapatkan hasil yang lebih akurat