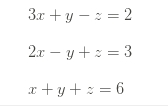Difference between revisions of "Metnum03-Muhammad Daffa Fachturrohman"
(→Tugas II) |
|||
| Line 66: | Line 66: | ||
Dengan demikian, saya menggunakan 3 persamaan aljabar yang ada sebagai berikut | Dengan demikian, saya menggunakan 3 persamaan aljabar yang ada sebagai berikut | ||
| − | [[File:1606107310523.jpg|600px] | + | [[File:1606107310523.jpg|600px]] |
Untuk menyelesaikan 3 persamaan tersebut, saya menggunakan Gauss Elimination. Didalam sistem OpenModelica sendiri, saya mengubahnya dalam bentuk matriks 3x3 yang dapat dilihat seperti kodingan saya dibawah ini | Untuk menyelesaikan 3 persamaan tersebut, saya menggunakan Gauss Elimination. Didalam sistem OpenModelica sendiri, saya mengubahnya dalam bentuk matriks 3x3 yang dapat dilihat seperti kodingan saya dibawah ini | ||
Revision as of 12:06, 23 November 2020
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
Assalamualaikum wr. wb.
Biodata Diri
Nama : Muhammad Daffa Fachturrohman
NPM : 1806181855
Agama : Islam
Program Studi : S1 Teknik Mesin Paralel
Contents
Pertemuan Pertama
Pada pertemuan pertama saya dengan Pak Ahmad Indra Siswantara, saya diminta untuk menginstall software OpenModelica yang bertujuan untuk mensimulasikan suatu sistem yang didistribusikan dalam bentuk kode sumber dan biner untuk penelitian.
Tugas I
Untuk Tugas Pertama yang saya dapat dari Pak Ahmad Indra Siswantara adalah membuat video pengaplikasian pada OpenModelica. Pada kesempatan kali ini, saya mengerjakan simulasi dari software OpenModelica ini bersumber dari buku yang saya gunakan selama pembelajaran Metode Numerik ini yaitu Numerical Methods for Engineers 7th Edition. Saya menerapkan regresi linear yang ada didalam buku tersebut yaitu di bab 17 tepatnya di example 17.1.
Disini saya hanya memasukkan data-data dari setiap variabel yang ada dan juga memasukkan formula-formula untuk menyelesaikan persamaan yang dibutuhkan yang datanya dari variabel yang telah saya masukkan kedalam sistem. Namun, ada sedikit kesalahan memasukkan data yang saya alami didalam video yang saya lampirkan dibawah. Tetapi OpenModelica ini sangat berguna untuk saya untuk menyelesaikan persamaan-persamaan yang ada didalam suatu sistem contohnya regresi linear yang saya kerjakan ini dibandingkan saya harus menghitungnya secara manual dan secara tertulis.
Berikut merupakan sumber yang saya gunakan dalam pengerjaan simulasi ini
Link Video
Berikut merupakan link video penjelasan saya dalam pengerjaan simulasi diatas dalam OpenModelica
Pertemuan Kedua
Pada pertemuan kali ini, setiap mahasiswa mata kuliah metode numerik 03 diminta untuk menjelaskan progres dari PRnya masing-masing kepada Pak Ahmad Indra Siswantara, namun saya tidak dipanggil untuk diminta menjelaskan kembali progres PR saya karena saya sudah mensimulasikan melalui OpenModelica dan saya juga sudah mengunggah video saya di youtube channel saya sendiri.
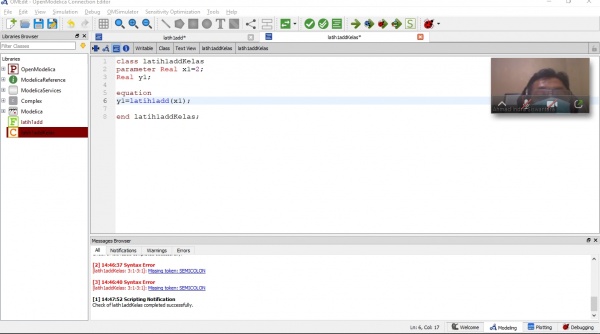
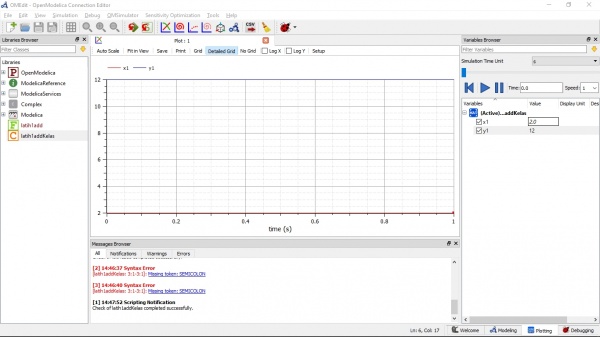
Pada pertemuan ini saya juga diajarkan untuk mensimulasikan kembali di OpenModelica sesuai dengan instruksi dari Pak Ahmad Indra Siswantara. Saya memasukkan persamaan kedalam kelas modelica yang saya buat untuk tipe Class dan juga Function, disitu saya diminta untuk memasukkan variabel-variabel yang telah disebutkan oleh Pak Ahmad Indra Siswantara, dan variabel-variabel sampai hasil simulasinya adalah sebagai berikut :
Tugas II
Pada pertemuan kedua dengan pak [Ahmad Indra Siswantara], saya diberikan tugas untuk menyelesaikan simulasi dari persamaan-presamaan aljabar simultan yaitu seperti Gauss Elimination, Gauss-Seidel, dan lainnya didalam OpenModelica.
Dengan demikian, saya menggunakan 3 persamaan aljabar yang ada sebagai berikut
Untuk menyelesaikan 3 persamaan tersebut, saya menggunakan Gauss Elimination. Didalam sistem OpenModelica sendiri, saya mengubahnya dalam bentuk matriks 3x3 yang dapat dilihat seperti kodingan saya dibawah ini
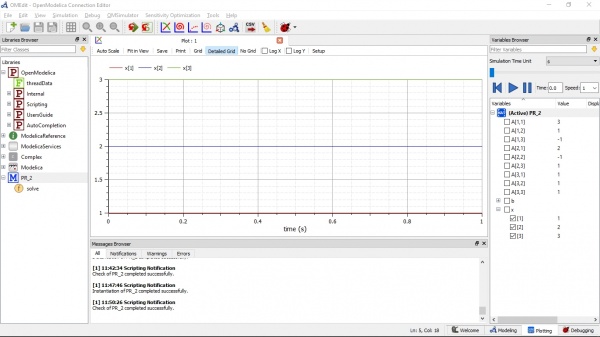
Untuk penyelesaiannya, saya mengugnakan perintah dari sistem OpenModelicanya sendiri, yaitu Modelica.Math.Matrices.solve(A,b) dan beberapa perintah baru yang saya pelajari dari beberapa sumber yang ada. Dan penyelesaiannya dari hasil simulasi saya adalah sebagai berikut
Sehingga ditemukan bahwa x = 1, y = 2, dan z = 3.