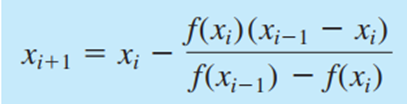Difference between revisions of "Metnum03-Dendy Dwi Rohma P J"
(→Pertemuan 2) |
(→Pertemuan 2) |
||
| Line 54: | Line 54: | ||
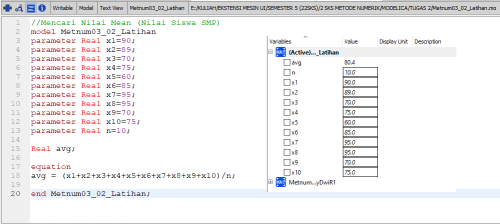
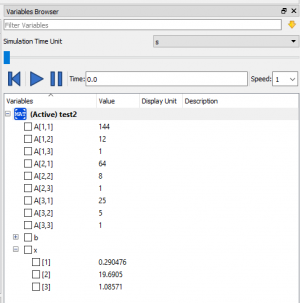
== Pertemuan 2 == | == Pertemuan 2 == | ||
| − | [[File:LatihanMean2.png|center]] | + | [[File:LatihanMean2.png|500px|center]] |
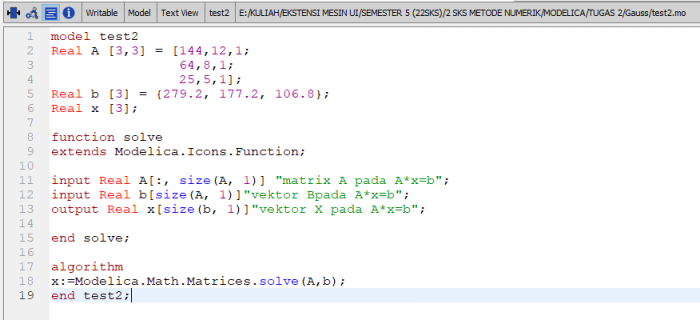
PR Eliminasi Gauss | PR Eliminasi Gauss | ||
| − | [[File:CodingGauss1.png| | + | [[File:CodingGauss1.png|700px|center]] |
| − | [[File:PlotingGauss2.png| | + | [[File:PlotingGauss2.png|300px|center]] |
[[File:ValidasiGauss.jpg|800px|center]] | [[File:ValidasiGauss.jpg|800px|center]] | ||
Revision as of 11:37, 23 November 2020
Assalamualaikum Warahmatullahi Wabarakatuh
Nama:Dendy Dwi Rohma P J
NPM: 1906435473
Pertemuan 1
1. Tugas_01_MetodeNumerik03
Dalam mencari nilai suatu akar dari suatu persamaan atau permasalahan yang ada, berbagai macam cara dan metode, berikut ini bermacam-macam metode yang dapat kita gunakan dalam mencari nilai suatu akar persamaan :
1. Metode Bagi dua (Bisection)
2. Metode False Position
3. Metode Secant
4. Metode Iterasi Titik Tetap
5. Metode Newton Raphson
Dalam kesempatan kali ini saya akan membahas tentang metode secant.
Pengertian Metode Secant
Metode secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimana kemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik.Tujuan dan Fungsi Tujuan metode secant adalah untuk menyelesaikan masalah yang terdapat pada metode Newton-Raphson yang terkadang sulit mendapatkan turunan pertama yaitu f'(x). Fungsi metode secant adalah untuk menaksirkan akar dengan menggunakan diferensi daripada turunan untuk memperkirakan kemiringan/slope.
Algoritma Metode Secant 1. Definisikan fungsi F(x) 2. Definisikan torelansi error (e) dan iterasi maksimum (n) 3. Masukkan dua nilai pendekatan awal yang di antaranya terdapat akar yaitu x0 dan x1,sebaiknya gunakan metode tabel atau grafis untuk menjamin titik pendakatannya adalah titik pendekatan yang konvergensinya pada akar persamaan yang diharapkan.
SOAL 1
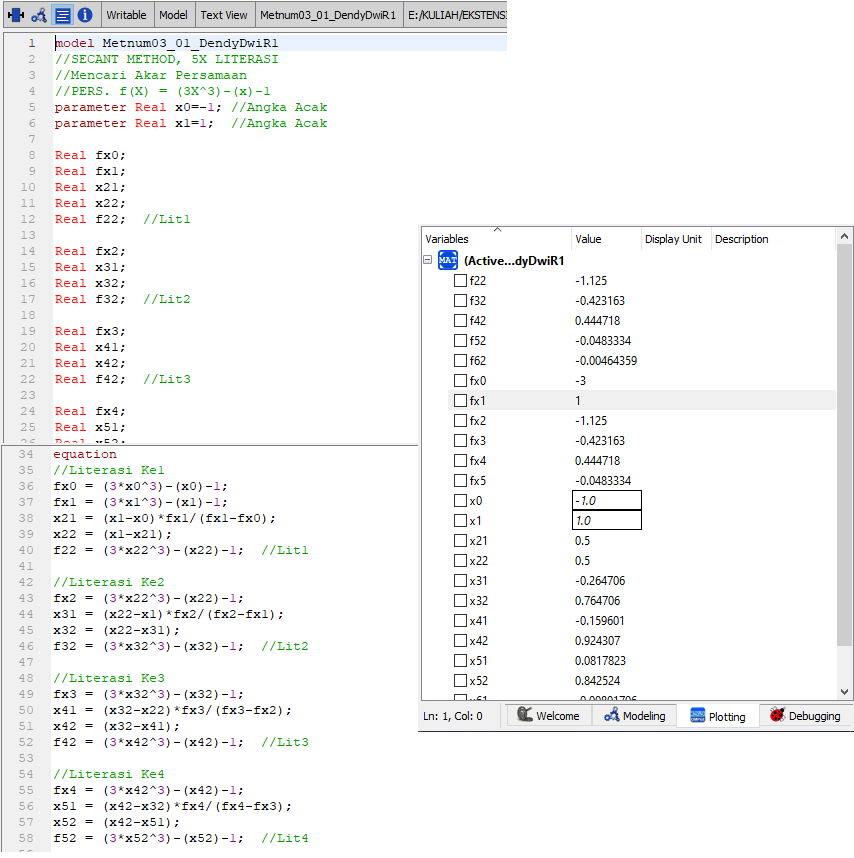
Cari Akar Persamaan dari Persamaan f(x) dengan Metode Secant Method pada Literasi ke 4? f(x) = 3x^3 -x -1
Asumsi:
x0 = -1
x = 1
Penjelasan menganai pemrograman Secant Method menggunakan OpenModelica terlampir dalam Link dibawah ini:
Link Youtube : https://www.youtube.com/watch?v=Bk_QtrInpks
Pertemuan 2
PR Eliminasi Gauss