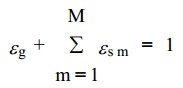Difference between revisions of "Hydrodynamic"
Agus.nuryadi (talk | contribs) (→Theory) |
Agus.nuryadi (talk | contribs) (→Theory) |
||
| Line 13: | Line 13: | ||
the '''averaging approach''' to derive equations that describe interpenetrating continua, the point variables are averaged over a region that is large compared with the particle spacing but much smaller than the flow domain. New field variables, the phasic volume fractions, are introduced to track the fraction of the averaging volume occupied by various phases. These are denoted by '''ε'''g for the fluid phase (also known as the void fraction) and '''ε'''sm for the mth solids phase. These volume fractions are assumed to be continuous functions of space and time. | the '''averaging approach''' to derive equations that describe interpenetrating continua, the point variables are averaged over a region that is large compared with the particle spacing but much smaller than the flow domain. New field variables, the phasic volume fractions, are introduced to track the fraction of the averaging volume occupied by various phases. These are denoted by '''ε'''g for the fluid phase (also known as the void fraction) and '''ε'''sm for the mth solids phase. These volume fractions are assumed to be continuous functions of space and time. | ||
| + | |||
| + | [[File:1.eq_theory.jpg|200px|thumb|left|alt text]] | ||
| + | |||
| + | M is the total number of solids phases. The effective (macroscopic) density of the gas phase is: | ||
Revision as of 09:38, 23 November 2020
Hydrodynamic modelling has the remarkable ability to synthesize data from various, relatively simple experiments (for example, the drag on an isolated sphere or the volatilization rate measured using a single layer of coal particles) and, thereby, to describe the time-dependent distribution of fluid and solids volume fractions, velocities, pressure, temperatures, and species mass fractions in industrial reactors. With such power also come several limitations that the user must bear in mind.
1. The accuracy of the model's predictions may be limited for a variety of reasons: incomplete formulation of the governing equations, insufficient knowledge of the constitutive relations, unsatisfactory numerical treatment of the governing partial differential equations, insufficient information on initial and boundary conditions, and the impracticality of using a large number of nodes to resolve all the fine details of the flow.
2. A limitation of hydrodynamic modeling is that an expert user is needed to conduct simulations and to analyze results. To assist the user, the present code resolves many of the difficulties in setting up simulations by using a special NAMELIST format in the input data file that reports input errors and allows comment lines. There is no limitation on the number of initial and boundary conditions. The code also does much run-time error reporting and has a graphical post-processor.
3. hydrodynamic modeling requires significant computer resources, although supercomputer facilities are not required. The availability of faster and cheaper computers has made hydrodynamic modeling more affordable.
Theory
The averaging approach and the mixture theory approach. In the averaging approach, the equations are derived by space, time, or ensemble averaging of the local, instantaneous balances for each of the phases. In the mixture theory approach, equations that are generalizations of single phase equations are postulated. Both approaches yield a similar set of balance equations that must be closed by specifying several constitutive relations, such as a fluid-phase equation of state, fluid-solids and solids-solids momentum transfer and heat transfer, and fluid and solids phase stress tensors. The principle of material frame-indifference, the second axiom of thermodynamics, material symmetry, and over-all balance equations for the mixture yield several useful restrictions on such constitutive relations.
the averaging approach to derive equations that describe interpenetrating continua, the point variables are averaged over a region that is large compared with the particle spacing but much smaller than the flow domain. New field variables, the phasic volume fractions, are introduced to track the fraction of the averaging volume occupied by various phases. These are denoted by εg for the fluid phase (also known as the void fraction) and εsm for the mth solids phase. These volume fractions are assumed to be continuous functions of space and time.
M is the total number of solids phases. The effective (macroscopic) density of the gas phase is: