Difference between revisions of "Using Spring-Mass Models to Determine the Dynamic Response of Two-Story Buildings Subjected to Lateral Loads by S.T. De la Cruz, M.A. Rodríguez & V. Hernández"
(→Terjemahan) |
Fadhli Ihsan (talk | contribs) (→Terjemahan) |
||
| Line 51: | Line 51: | ||
[[File:2020-05-08 01_45_01-Microsoft Edge.png|| 300px]] | [[File:2020-05-08 01_45_01-Microsoft Edge.png|| 300px]] | ||
| + | |||
| + | 3.1.2. Respons Perpindahan Menggunakan Merangkat Lunak Komersial | ||
| + | |||
| + | Data di atas dapat diimplementasikan dengan cepat ke dalam perangkat lunak komersial seperti ADINA (Bathe, 1996). | ||
| + | Di ADINA, peredam viskos dan pegas (koefisien kekakuan) dapat dimasukkan sebagai elemen linier, membuat pemodelan sangat sederhana (De la Cruz et al., 2009). Selain itu, sejarah waktu | ||
| + | respons yang diperoleh dengan ADINA sama dengan yang diperoleh pada ayat 3.1.2. | ||
| + | |||
| + | 3.2. Pengujian Meja Goyang | ||
| + | |||
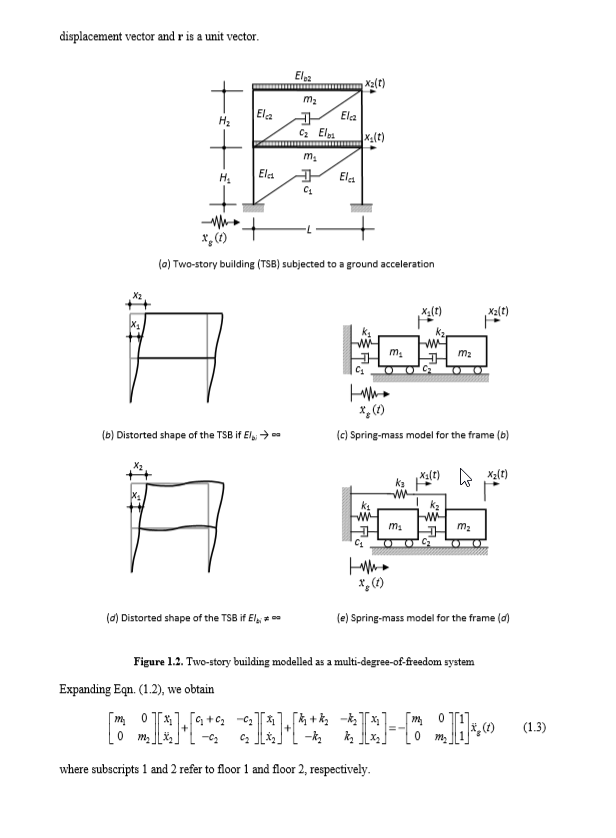
| + | SMM ditunjukkan pada Gambar. 1.2c dapat dibangun sehingga model fisik dari TSB yang sebenarnya (baik SB atau MRF) | ||
| + | dapat diuji. Selain itu, perilaku nonlinear (mis., Kekakuan bi-linear) dapat disimulasikan dengan menggunakan | ||
| + | perangkat gesekan yang melekat pada mata air (De la Cruz et al., 2010). | ||
== Judul .... Artikel2 1 hasil diskusi == | == Judul .... Artikel2 1 hasil diskusi == | ||
== Judul .... Artikel3 1 hasil diskusi == | == Judul .... Artikel3 1 hasil diskusi == | ||
== Judul .... Artikel4 1 hasil diskusi == | == Judul .... Artikel4 1 hasil diskusi == | ||
Revision as of 02:09, 8 May 2020
<- back to Studi kasus komputasi teknik
Contents
Knowledge Base
Case Study
Terjemahan
Applicaiton
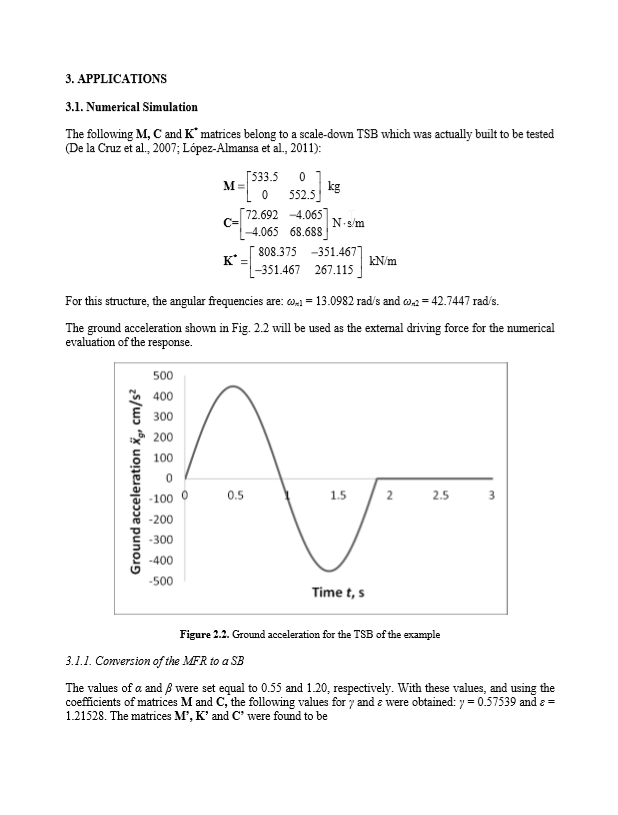
Matriks M, C dan K * berikut milik TSB skala-turun yang sebenarnya dibangun untuk diuji
Untuk struktur ini, frekuensi sudutnya adalah ωn1 = 13.0982 rad/s and ωn2 = 42.7447 rad/s.
Akselerasi ground yang ditunjukkan pada Gambar 2.2 akan digunakan sebagai kekuatan pendorong eksternal untuk evaluasi numerik dari respons.
3.1.1. Konversi MFR ke SB
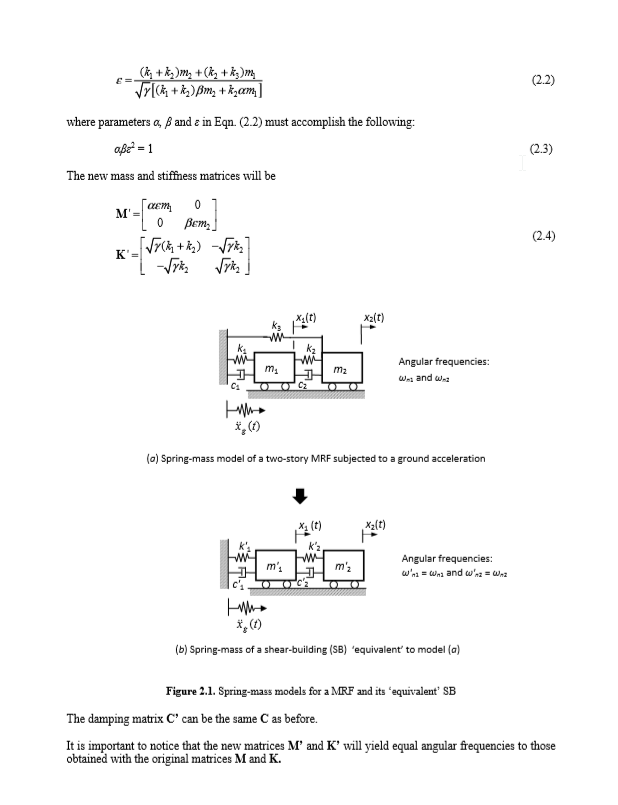
Nilai α dan β ditetapkan masing-masing sebesar 0,55 dan 1,20. Dengan nilai-nilai ini, dan menggunakan koefisien matriks M dan C, nilai-nilai berikut untuk γ dan ε diperoleh: γ = 0,57539 dan ε = 1,21528. Matriks M ’, K’ dan C ’ditemukan.
Untuk struktur 'yang dikonversi' ini, frekuensi sudutnya adalah: ω'n1 = 13.0811 rad / s dan ω'n2 = 43.3512 rad / s
3.1.2
3.1.2. Respons Perpindahan Menggunakan Merangkat Lunak Komersial
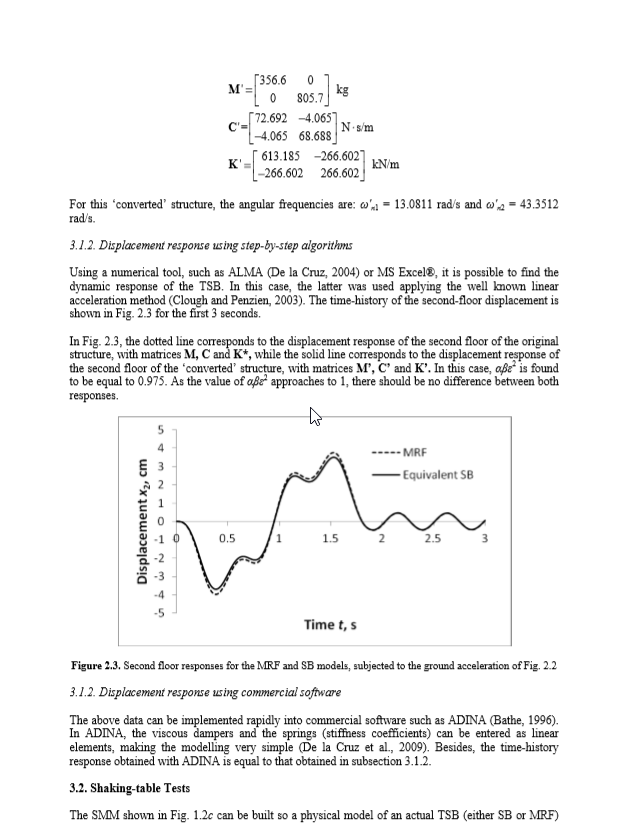
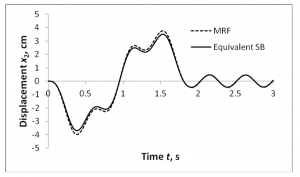
Data di atas dapat diimplementasikan dengan cepat ke dalam perangkat lunak komersial seperti ADINA (Bathe, 1996). Di ADINA, peredam viskos dan pegas (koefisien kekakuan) dapat dimasukkan sebagai elemen linier, membuat pemodelan sangat sederhana (De la Cruz et al., 2009). Selain itu, sejarah waktu respons yang diperoleh dengan ADINA sama dengan yang diperoleh pada ayat 3.1.2.
3.2. Pengujian Meja Goyang
SMM ditunjukkan pada Gambar. 1.2c dapat dibangun sehingga model fisik dari TSB yang sebenarnya (baik SB atau MRF) dapat diuji. Selain itu, perilaku nonlinear (mis., Kekakuan bi-linear) dapat disimulasikan dengan menggunakan perangkat gesekan yang melekat pada mata air (De la Cruz et al., 2010).