Difference between revisions of "Using Spring-Mass Models to Determine the Dynamic Response of Two-Story Buildings Subjected to Lateral Loads by S.T. De la Cruz, M.A. Rodríguez & V. Hernández"
(→Terjemahan) |
(→Terjemahan) |
||
| Line 29: | Line 29: | ||
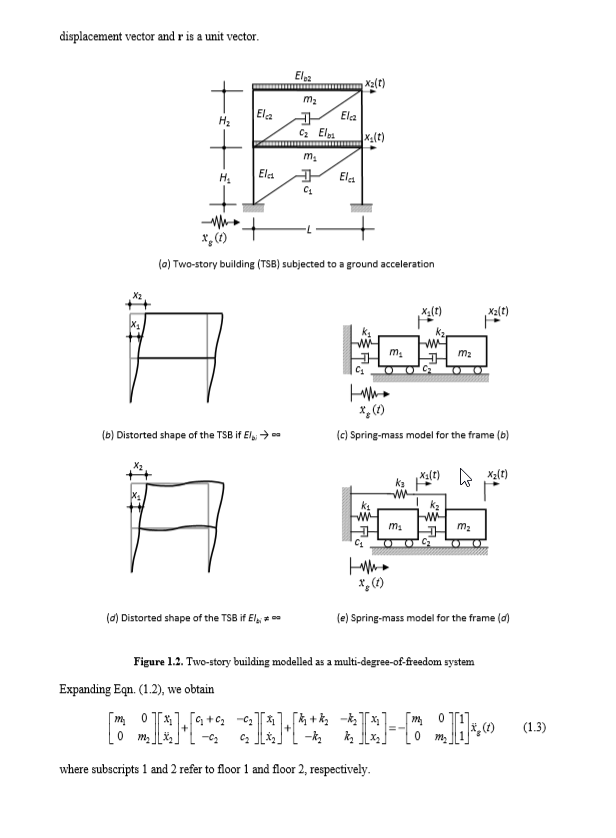
Matriks M, C dan K * berikut milik TSB skala-turun yang sebenarnya dibangun untuk diuji | Matriks M, C dan K * berikut milik TSB skala-turun yang sebenarnya dibangun untuk diuji | ||
| − | [[File:2020-05-08 01_13_37-Microsoft Edge.png|| | + | [[File:2020-05-08 01_13_37-Microsoft Edge.png|| 300px]] |
Untuk struktur ini, frekuensi sudutnya adalah ωn1 = 13.0982 rad/s and ωn2 = 42.7447 rad/s. | Untuk struktur ini, frekuensi sudutnya adalah ωn1 = 13.0982 rad/s and ωn2 = 42.7447 rad/s. | ||
| Line 43: | Line 43: | ||
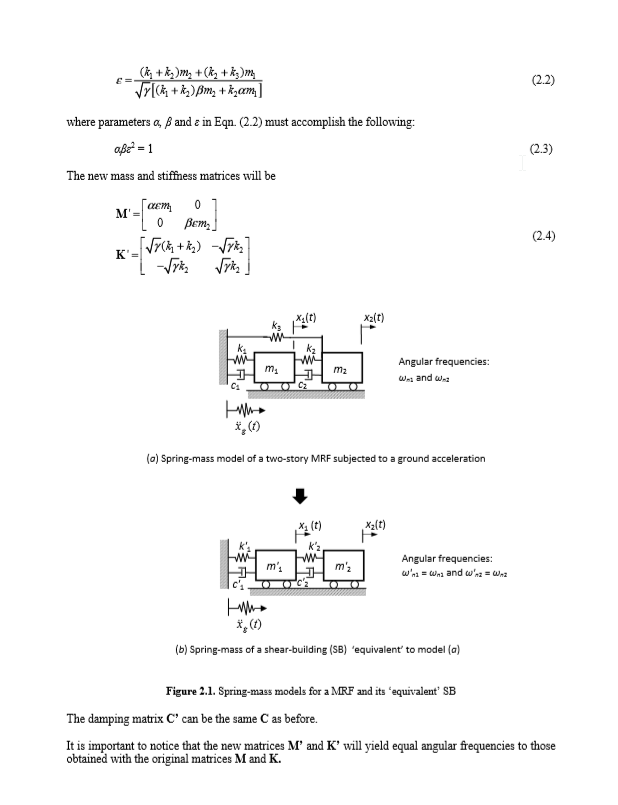
Nilai α dan β ditetapkan masing-masing sebesar 0,55 dan 1,20. Dengan nilai-nilai ini, dan menggunakan koefisien matriks M dan C, nilai-nilai berikut untuk γ dan ε diperoleh: γ = 0,57539 dan ε = 1,21528. Matriks M ’, K’ dan C ’ditemukan. | Nilai α dan β ditetapkan masing-masing sebesar 0,55 dan 1,20. Dengan nilai-nilai ini, dan menggunakan koefisien matriks M dan C, nilai-nilai berikut untuk γ dan ε diperoleh: γ = 0,57539 dan ε = 1,21528. Matriks M ’, K’ dan C ’ditemukan. | ||
| − | [[File:3.1.1.Conversion of the MFR to a SB.JPG]] | + | [[File:3.1.1.Conversion of the MFR to a SB.JPG || 300px]] |
Untuk struktur 'yang dikonversi' ini, frekuensi sudutnya adalah: ω'n1 = 13.0811 rad / s dan ω'n2 = 43.3512 rad / s | Untuk struktur 'yang dikonversi' ini, frekuensi sudutnya adalah: ω'n1 = 13.0811 rad / s dan ω'n2 = 43.3512 rad / s | ||
| Line 50: | Line 50: | ||
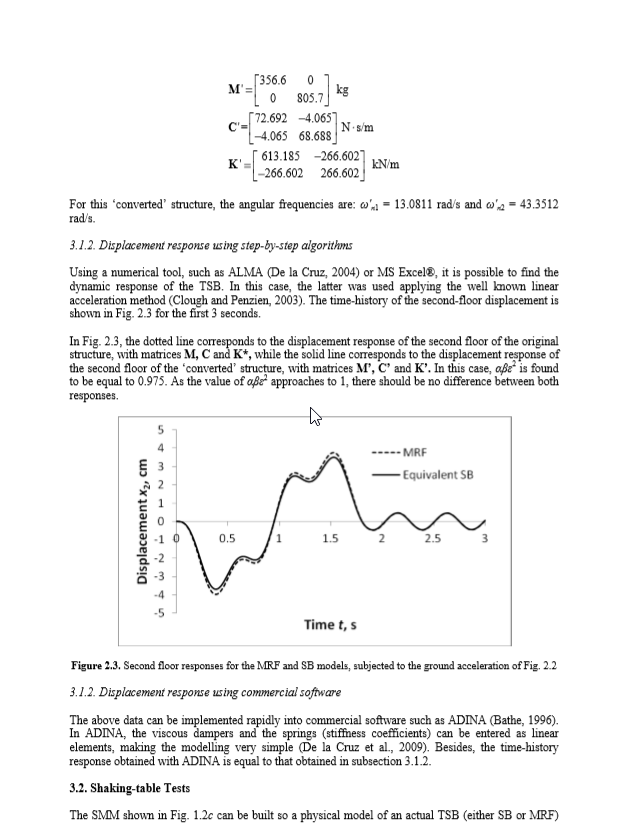
3.1.2 | 3.1.2 | ||
| − | [[File:2020-05-08 01_45_01-Microsoft Edge.png|| | + | [[File:2020-05-08 01_45_01-Microsoft Edge.png|| 300px]] |
== Judul .... Artikel2 1 hasil diskusi == | == Judul .... Artikel2 1 hasil diskusi == | ||
== Judul .... Artikel3 1 hasil diskusi == | == Judul .... Artikel3 1 hasil diskusi == | ||
== Judul .... Artikel4 1 hasil diskusi == | == Judul .... Artikel4 1 hasil diskusi == | ||
Revision as of 02:00, 8 May 2020
<- back to Studi kasus komputasi teknik
Contents
Knowledge Base
Case Study
Terjemahan
Applicaiton
Matriks M, C dan K * berikut milik TSB skala-turun yang sebenarnya dibangun untuk diuji
Untuk struktur ini, frekuensi sudutnya adalah ωn1 = 13.0982 rad/s and ωn2 = 42.7447 rad/s.
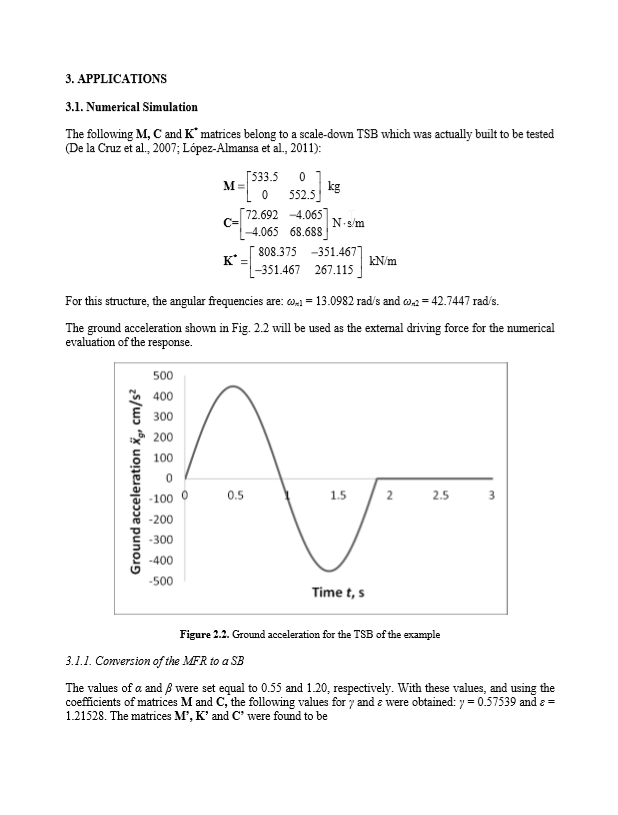
Akselerasi ground yang ditunjukkan pada Gambar 2.2 akan digunakan sebagai kekuatan pendorong eksternal untuk evaluasi numerik dari respons.
3.1.1. Konversi MFR ke SB
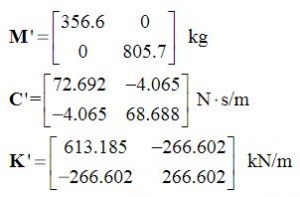
Nilai α dan β ditetapkan masing-masing sebesar 0,55 dan 1,20. Dengan nilai-nilai ini, dan menggunakan koefisien matriks M dan C, nilai-nilai berikut untuk γ dan ε diperoleh: γ = 0,57539 dan ε = 1,21528. Matriks M ’, K’ dan C ’ditemukan.
Untuk struktur 'yang dikonversi' ini, frekuensi sudutnya adalah: ω'n1 = 13.0811 rad / s dan ω'n2 = 43.3512 rad / s
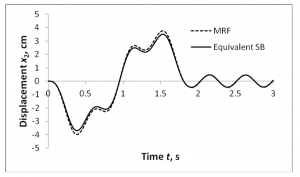
3.1.2