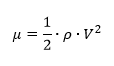Difference between revisions of "Elita Kabayeva"
| Line 200: | Line 200: | ||
Dengan μ dan V berturut-turut adalah viskositas dinamik dan kecepatan. Hal ini menyebabkan tekanan dinamik cenderung lebih konstan ketika berada pada fully developed region dikarenakan perubahan kecepatan pada daerah tersebut sangat kecil, namun sebaliknya tekanan dinamik cenderung mengalami perubahan yang cukup besar ketika berada pada entrance region. | Dengan μ dan V berturut-turut adalah viskositas dinamik dan kecepatan. Hal ini menyebabkan tekanan dinamik cenderung lebih konstan ketika berada pada fully developed region dikarenakan perubahan kecepatan pada daerah tersebut sangat kecil, namun sebaliknya tekanan dinamik cenderung mengalami perubahan yang cukup besar ketika berada pada entrance region. | ||
| + | |||
| + | |||
| + | == PERTEMUAN III MEKANIKA FLUIDA (Selasa, 04/07/2020) == | ||
| + | |||
| + | Pada pertemuan ini dijelaskan mengenai ''governing equation'' untuk aliran fluida. Sebagai medium penjelasannya, digunakanlah soal berikut ; | ||
| + | |||
| + | [[File:Laminar_flow_through_the_parallel-_plate_analytical_sol_1.png|centre|400px]] | ||
| + | |||
| + | [[File:Laminar_flow_through_the_parallel-_plate_analytical_sol_2.png|centre|400px]] | ||
| + | |||
| + | [[File:Laminar_flow_through_the_parallel-_plate_analytical_sol_5.png|centre|400px]] | ||
| + | |||
| + | [[File:Laminar_flow_through_the_parallel-_plate_analytical_sol_6.png|centre|400px]] | ||
| + | |||
| + | Dari soal tersebut, dapat dijelaskan bahwa penggunaan ''governing equation'', pada kasus ini adalah Navier-Stokes, dapat dimodifikasi sesuai dengan kondisi pada soal. Navier-stokes dapat diterapkan pada dua dimensi (seperti pada soal) dan dalam kondisi ''velocity profile'' seperti apapun. | ||
| + | |||
| + | Selain membahas mengenai ''governing equation'' , pada pertemuan ini juga dibahas mengenai hubungan Reynolds Number dengan Gaya Inersia dan Friction Force. dijelaskan bahwa, semakin tinggi gaya inersia, akan semakin tinggi pula tendensi terjadinya perubahan jenis aliran dari laminer ke turbulen. Hal ini disebabkan karena semkain naiknya nilai inersia, akan berpengaruh kepada terjadinya ''Eddy'' pada aliran (atau bisa juga disebut sebagai olakan. Olakan-olakan ini akan mengubah aliran laminer yang teratur menjadi aliran turbulen yang bentuknya acak dan cenderung memiliki ''vortex''. | ||
| + | |||
| + | Disebutkan pula bahwa viskositas memiliki hubungan dengan tegangan geser. Semakin tinggi viskositas, entrance length akan semakin pendek atau semakin dekat dengan hulu aliran. Hal ini disebabkan karena, semakin kental (yang berarti semakin tinggi viskositasnya) suatu fluida, alirannya akan sulit untuk memiliki olakan ataupun vortex. Karena, dengan semakin tingginya viskositas, friction force akan semakin tinggi pula yang akan meningkatkan tegangan geser antar lapisan fluidanya. | ||
| + | |||
| + | |||
| + | |||
| + | == PERTEMUAN IV MEKANIKA FLUIDA (Rabu, 04/08/2020) == | ||
| + | |||
| + | Pada kesempatan ini dijelaskan lebih lanjut mengenai macam-macam aliran fluida berdasarkan reynolds numbernya. Terdapat tiga jenis fluida yang bisa dibagi berdasarkan nilai Re. Yakni ; | ||
| + | |||
| + | 1. Laminar Flow ; nilai Re untuk laminar flow adalah kurang lebih dibawah 1400. Aliran laminar ini memiliki karakteristik yang dikenal sebagai fluida yang ideal dan dapat dikatakan sebagai fluida yang memiliki losses paling sedikit. | ||
| + | |||
| + | |||
| + | 2. Transition Flow ; untuk fluida yang memiliki Re antara 1400 hingga 4000, dinamakan aliran transisi. Disebut demikian karena aliran ini masih memiliki karakteristik dari laminar flow dan sudah memiliki elemen-elemen karakteristik dari turbulent flow. | ||
| + | |||
| + | |||
| + | 3. Turbulent Flow ; Fluida dengan Re diatas 4000 dikategorikan sebagai turbulent flow. Meskipun flow ini dianggap sebagai aliran yang tidak ideal, ini adalah aliran yang sesungguhnya berada pada dunia nyata. Aliran ini bersifat unsteady, complex, dan three-dimensional sehingga untuk melakukan analisis terhadap aliran ini, diperlukan konsep dan komputasi yang lebih rumit jika dibandingkan dengan laminar flow yang bisa menggunakan asumsi untuk fluida Bernoulli. | ||
| + | |||
| + | |||
| + | |||
| + | Selain ini, dijelaskan juga bahwa terdapat bermacam-macam kecepatan pada turbulent flow serta karakteristik dari turbulent flow itu sendiri. Dibahas juga mengenai apa-apa saja yang perlu diperhatikan pada turbulent flow dan faktor apa yang memengaruhi pressure drop pada aliran turbulen. | ||
| + | |||
| + | Dilakukan pula simulasi CFD untuk aliran turbulen dan ditunjukkan perbedaan ''velocity profile'' pada aliran turbulen dan laminar sebagai berikut ; | ||
| + | [[File:Aliran_turbul-lam.PNG|centre|600px|thumb]] | ||
| + | |||
| + | |||
| + | |||
| + | == PERTEMUAN V MEKANIKA FLUIDA (Selasa, 04/14/2020) == | ||
| + | |||
| + | Pada kesempatan ini, diminta untuk membuat artikel dengan referensi yang mengacu pada [[Soal-jawab Mekanika Fluida]] untuk nomor 1 hingga 6. Artikel tersebut terlampir sebagai berikut ; | ||
| + | |||
| + | |||
| + | == QUIZ 1 == | ||
| + | |||
| + | '''ARTIKEL I ; Penggunaan Navier-Stokes untuk Aliran Laminer 2 Dimensi ''' | ||
| + | |||
| + | Dalam kasus dimana kecepatan vertikal (v) sama dengan nol dan komponen kecepatan horizontal (u) bergantung terhadap x, dapat dikatakan bahwa komponen u adalah fungsi dari y. | ||
| + | |||
| + | |||
| + | Hal ini dapat di buktikan dengan menggunakan rumus kontinuitas dari persamaan Navier-Stokes untuk aliran dua dimensi; | ||
| + | |||
| + | ''Du/dx + dv/dy = 0 | ||
| + | '' | ||
| + | ''Du/dx + 0 = 0 | ||
| + | '' | ||
| + | ''Du/dx = 0'' | ||
| + | |||
| + | Kemudian, dengan menggunakan kondisi ini pada rumus momentum x, diketahui bahwa | ||
| + | |||
| + | ''D2u/dy2 = 1/μ dp/dx'' | ||
| + | |||
| + | |||
| + | Dapat disimpulkan bahwa ketentuan untuk kekalan momentum pada kasus ini adalah persamaan gaya ''shear'' dan ''pressure''. | ||
| + | |||
| + | Dengan menggunakan dua kali integral, di dapatkan kecepatan horizontal u terhadap y ; | ||
| + | |||
| + | |||
| + | ''U(y) = 1/2μ (dp/dx) y2 + C1y + C2'' | ||
| + | |||
| + | |||
| + | Dan kondisi batas untuk menentukan C1 serta C2 adalah ; | ||
| + | |||
| + | |||
| + | ''U = 0'' untuk y = H/2 (no slip) | ||
| + | |||
| + | |||
| + | ''Du/dy = 0'' untuk y = 0 (simetris) | ||
| + | |||
| + | |||
| + | Untuk kondisi simetris, didapatkan '''C1 = 0.''' | ||
| + | |||
| + | |||
| + | Maksud dari kondisi ''no slip'' disini adalah fluida dianggap sebagai fluida viskos. Diasumsikan bahwa pada ''solid boundary'', fluida akan memilii kecepatan 0 terhadap dinding pipa. | ||
| + | |||
| + | Menggunakan metode subtitusi, akan di dapatkan '''nilai C2 = -1/2μ (dp/dx) (H/2)2.''' | ||
| + | |||
| + | |||
| + | Dengannya profil kecepatan u(y) akan menjadi ; | ||
| + | |||
| + | ''U (y) = 3/2 H2/12μ (-dp/dx) (1-(y2/(H/2)2) | ||
| + | '' | ||
| + | |||
| + | |||
| + | Gradien kecepatan dp/dx disini bernilai negatif karena pressure berkurang disepanjang aliran. Hal ini disebabkan karena adanya ''pressure drop''. | ||
| + | |||
| + | |||
| + | Untuk aplikasinya, soal ini dapat digunakan sebagai kasus simulasi untuk aliran air pada pipa secara dua dimensi. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''ARTIKEL II ; Pengaruh Viskositas dan Kecepatan Inlet pada Entrance Length Aliran Laminer''' | ||
| + | |||
| + | Pada kasus ini dapat dilihat setelah dilakukan perhitungan bahwa, baik untuk kasus A dimana kecepatan inlet dipertahankan dan viskositas diubah (ada dua jenis), | ||
| + | maupun kasus B dimana viskositas dipertahankan dan kecepatan inlet diubah (ada dua jenis), | ||
| + | |||
| + | keduanya akan memberikan dua hasil ''entrance length'' yang sama dan secara tidak langsung, memberikan Reynold’s number yang sama (maksudnya, hanya akan ada dua nilai LE berbeda untuk empat kondisi ini). | ||
| + | |||
| + | |||
| + | Hal ini disebabkan karena, LE sebanding dengan Re. Maka perubahan yang terjadi pada Re akan menyebabkan perubahan secara proporsional pada LE. | ||
| + | |||
| + | |||
| + | Kasus dengan Re dan LE ini juga berpengaruh terhadap ''velocity profile'' nya. | ||
| + | |||
| + | |||
| + | Pada bagian A, kasus pertama, dimana kecepatan inlet adalah 0.01 m/s dan viskositas dinamik = 4 x 10-5 kg/m.s memiliki profil kecepatan yang berbeda saat viskositas dinamiknya diubah menjadi 10-5 kg/m.s | ||
| + | |||
| + | |||
| + | Hal ini disebabkan karena pada saat kedua kondisi tersebut diberikan gaya inersia yang sama, fluida dengan viskositas dinamik yang lebih tinggi akan memberikan gaya friksi yang lebih besar, sehingga menghasilkan momentum fluida. | ||
| + | Mengakibatkan terbentuknya kondisi ''fully developed'' dengan lebih cepat. | ||
| + | |||
| + | Mengapa? Karena, aliran fluida lebih pelan dan stabil jika dibanidngkan dengan fluida yang memiliki viskositas dinamik lebih kecil (yang akan memiliki LE lebih panjang). | ||
| + | |||
| + | |||
| + | Untuk bagian B, hal serupa terjadi. Yang menjadi perhatian adalah bagaimana fluida dengan viskositas dinamik yang sama namun memiliki kecepatan inlet berbeda, akan memberikan hasil yang serupa dengan kasus A (dimana kecepatan inlet sama dan viskositas dinamik berbeda). | ||
| + | |||
| + | |||
| + | Ini dapat dijelaskan dengan menggunakan persamaan Navier-Stokes untuk aliran dua dimensi ; | ||
| + | |||
| + | |||
| + | '''Inersia = -pressure + friksi''' | ||
| + | |||
| + | |||
| + | Yang mana, gaya inersia sebanding dengan gaya friksi (dan gaya inersia sebanding dengan kecepatan). | ||
| + | |||
| + | |||
| + | Aplikasi untuk kasus ini akan berguna untuk membuat simulasi mengenai berapa ''pressure drop'' serta sejauh apa fluida baru akan stabil dalam beberapa kondisi tertentu. | ||
| + | |||
| + | |||
| + | |||
| + | '''ARTIKEL III ; Karakter Profil Kecepatan Laminer vs Turbulen''' | ||
| + | |||
| + | |||
| + | Pada kasus ini, terlihat dengan jelas perbedaan profil kecepatan laminer dan turbulen. | ||
| + | Pada aliran laminer, profil kecepatan berbentuk parabola, sedangkan untuk aliran turbulen, pada area ''fully developed'' , profil kecepatan cenderung berbentuk datar. | ||
| + | |||
| + | |||
| + | Hal ini disebabkan karena viskositas turbulen yang tinggi berdifusi ke aliran. Atau dapat juga dijelaskan bahwa akibat dari nilai Reynolds number yang tinggi, | ||
| + | distribusi pada aliran turbulen terjadi secara acak. Yang disebabkan karena adanya tegangan geser yang besar. | ||
| + | |||
| + | Tegangan geser ini menjadi parameter yang cukup penting untuk mencari distribusi kecepatan pada aliran turbulen karena, akan adanya ‘energi yang tertinggal’ di dinding. | ||
| + | Energi yang tertinggal ini akan menyebabkan persebaran kecepatan pada aliran turbulen akan cenderung datar. | ||
| + | |||
| + | |||
| + | [[File:LvsT.png|centre|600px|thumb]] | ||
| + | |||
| + | |||
| + | |||
| + | '''ARTIKEL IV ; Pengaruh Sudut Elevasi pada Pipeline untuk Aliran Laminer''' | ||
| + | |||
| + | |||
| + | Dalam perancangan suatu ''pipeline'' tentu ''pressure drop'' menjadi salah satu parameter vital yang harus dikonsiderasi untuk menentukan bentuk isometrik ''pipeline''. | ||
| + | Rugi-rugi tekanan yang terlalu besar akan menyebabkan fluida tidak dapat mengalir hingga ke tujuannya tanpa bantuan dari pompa. | ||
| + | |||
| + | |||
| + | Hal yang perlu diperhatikan dalam ''pressure drop'' adalah bahwa untuk suatu kondisi fluida yang sama, apabila sudut elevasi pipeline berubah, | ||
| + | maka ''pressure drop'' yang didapatkan tidak akan sama. | ||
| + | |||
| + | |||
| + | |||
| + | Untuk memberikan suatu bukti akan klaim ini, dimisalkan suatu fluida dengan aliran laminer yang berada pada dua kondisi. | ||
| + | |||
| + | |||
| + | Kondisi pertama adalah fluida mengalir pada ''pipeline'' yang lurus horizontal. Sedangkan kondisi kedua, fluida mengalir pada ''pipeline'' yang memiliki sudut elevasi θ. | ||
| + | |||
| + | '''Pada dua kondisi ini, fluida memiliki viskositas, massa jenis, dan flowrate yang sama.''' | ||
| + | |||
| + | |||
| + | |||
| + | Dalam hukum Poiseulle, dinyatakan bahwa untuk ''flowrate'', viskositas, dan massa jenis yang sama, ''pressure drop'' akan dikurangi oleh gamma dikali panjang dikali sinus dari sudut elevasi. | ||
| + | Sehingga, pada kondisi pipa horizontal ''pressure drop'' yang didapatkan akan lebih kecil jika dibandingkan dengan pada kondisi pipa menanjak (memiliki sudut elevasi). | ||
| + | |||
| + | |||
| + | |||
| + | Perlu diperhatikan, jika ''pipeline'' berada pada kondisi turunan, gravitasi akan membantu pergerakan fluida, | ||
| + | sehingga ''pressure drop'' yang lebih kecil akan di dapatkan (sin θ < 0) . Jika ''pipeline'' berada pada kondisi menanjak, pressure drop yang didapatkan akan lebih besar (sin θ > 0). | ||
| + | |||
| + | |||
| + | Dengan penjelasan demikian, maka terlihat bahwa untuk perancangan ''pipeline'' di lapangan sangat di pengaruhi oleh sudut elevasi. | ||
| + | Sehingga setelah dilakukan kalkulasi, akan diketahui di titik-titik mana saja akan diperlukan pompa untuk mengatasi ''pressure drop'' yang terjadi. | ||
| + | |||
| + | |||
| + | Aplikasi di lapangan untuk ini ada pada perancangan ''pipeline'' migas. | ||
| + | |||
| + | |||
| + | |||
| + | '''ARTIKEL V ; Turbulen dan Pengaruhnya pada Aliran''' | ||
| + | |||
| + | |||
| + | Terdapat dua jenis aliran. Yakni laminer dan turbulen. Pada kehidupan sehari-hari, jenis aliran turbulen akan lebih umum ditemui dibanding laminer. | ||
| + | Yang khas dari aliran turbulen adalah karakteristiknya yang cenderung acak. Hal ini terjadi baik pada kecepatan, ''pressure'', ''shear stress'', temperatur, | ||
| + | dan variabel-variabel lain yang memiliki medan. | ||
| + | |||
| + | |||
| + | '''Selain itu, aliran turbulen di sebabkan oleh ''vorticity'' 3 dimensi yang juga bergerak acak. ''Vorticity'' adalah perputaran partikel fluida. | ||
| + | ''' | ||
| + | |||
| + | |||
| + | |||
| + | Dapat di ''highlight'' pula, bahwa pada aliran turbulen, ''shear stress'' dan ''pressure drop'' akan jauh lebih tajam dibanding dengan aliran laminer. | ||
| + | Hal ini disebabkan karena sublayer viskos pada aliran turbulen sangat tipis. Kondisi ini menyebabkan ketidak sempurnaan dari dinding pipa akan masuk ke sublayer dan memengaruhi karakteristik aliran. | ||
| + | |||
| + | |||
| + | Viskos sub layer adalah lapisan tipis dekat dinding yg kontak langsung dengan dinding aliran fluida pd aliran turbulen dgn turbulensi minimal yg nantinya energi turbulen itu diubah mnjadi energi panas. | ||
| + | |||
| + | |||
| + | Aliran turbulen ''fully developed'' pada pipa juga merupakan aliran axisymmetric. Yang berarti pola aliran identik pada setiap bidang yang melewati suatu garis lurus. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''ARTIKEL VI ; Rugi-rugi Tekanan pada Laminer dan Turbulen''' | ||
| + | |||
| + | |||
| + | Sering disebutkan bahwa aliran laminer merupakan aliran fluida yang dianggap ideal. Sedangkan aliran turbulen adalah aliran non-ideal yang banyak ditemui di kehidupan sehari-hari. | ||
| + | |||
| + | Aliran laminer dianggap sebagai aliran fluida ideal, salah satu nya adalah karena pressure drop atau rugi-rugi tekanan yang terjadi pada aliran ini sangat kecil. | ||
| + | |||
| + | '''Untuk suatu kondisi yang sama, rugi-rugi tekanan pada aliran turbulen dapat meningkat tajam jika dibandingkan dengan laminer. | ||
| + | ''' | ||
| + | |||
| + | |||
| + | Hal ini disebabkan karena adanya pengaruh dari ''friction force'' yang terjadi. Pada aliran turbulen, nilai ''friction force'' ini sangat besar disebabkan oleh karakteristik aliran tersebut yang cenderung acak. | ||
| + | Semakin meningkatnya ''friction force'', maka rugi-rugi tekanan yang didapatkan akan semakin besar. | ||
| + | |||
| + | |||
| + | Dengan penjelasan tersebut, pada kehidupan sehari-hari, sudah menjadi hal yang umum untuk membuat aliran mendekati kondisi laminer (sedekat yang dimungkinkan) salah satunya adalah untuk menekan terjadinya rugi-rugi tekanan yang terlalu tinggi. | ||
Revision as of 08:20, 4 May 2020
Contents
BIODATA DIRI
Nama : Elita Kabayeva
NPM : 1906435486
Email : elita.kabayeva@ui.ac.id
Jurusan : Teknik Mesin
PERTEMUAN I MEKANIKA FLUIDA (Selasa, 03/31/2020)
Pertemuan hari ini (03/31/2020) dimulai dengan penjelasan singkat mengenai teori Aliran Fluida Viskos dalam Pipa yang disampaikan oleh bang Muhammad Hilman Gumelar (bang Edo) via aplikasi Zoom. Penjelasan tersebut berlangsung selama kurang lebih tiga puluh menit dan kemudian dilanjutkan dengan praktek menggunakan software CFDSOF.
SIMULASI CFDSOF
Dalam pertemuan kali ini bang Edo sudah memiliki perhitungan studi kasus mengenai aliran fluida viskos dalam excel yang terlebih dahulu ditampilkan dan simulai CFDSOF akan mengacu pada data-data pada studi kasus tersebut.
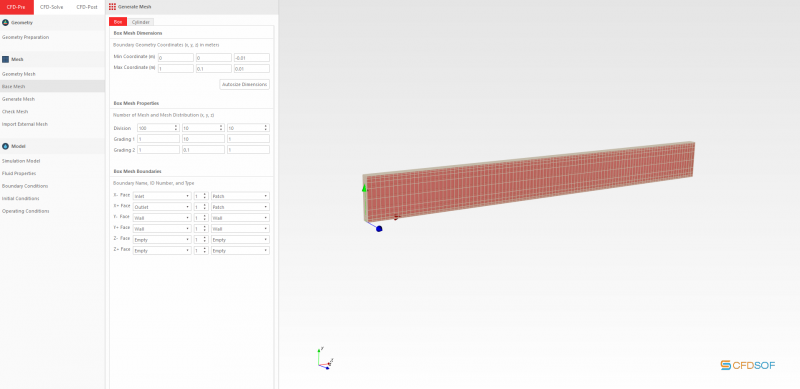
Masuk pada CFDSOF, yang pertama dilakukan adalah menentukan base mesh. Digunakan tipe mesh box, karena dalam simulasi ini, yang digunakan adalah visualisasi 2 Dimensi. Karena hal itu juga, pada saat mengisi Box Mesh Dimension, yang diisi adalah dimensi pada sumbu X dan Y saja. Sedangkan untuk sumbu Z, diisi dengan nilai sekecil mungkin (pada kesempatan ini digunakan nilai -0,01<Z<0,01. Kemudian pada pengisian Box Mesh Properties, untuk division, dicari rasio pada X dan Y yang akan menghasilkan grid simetris, sedangkan untuk sumbu Z dapat diabaikan. Setelah mengisi division, untuk grading, diisi pada sumbu Y dengan Grading 1 sebesar 10 dan Grading 2 sebesar 0.1. Hal ini dilakukan dengan paham bahwa fluida yang berkontak dengan dinding pipa akan memiliki v = 0 dan gaya geser tinggi. Grading dilakukan agar pada saat simulasi, didapatkan hasil yang lebih teliti pada bagian yang berkontak dengan pipa. Setelah itu, dilakukan pemilihan untuk properti masing-masing sumbu dengan X- Inlet, X+ Outlet, Y- & Y+ wall, serta Z- & Z+ empty.
Pada opsi Generate Mesh, dilakukan pemindahan koordinat mesh agar berada di dalam Box Mesh yang akan disimulasikan.
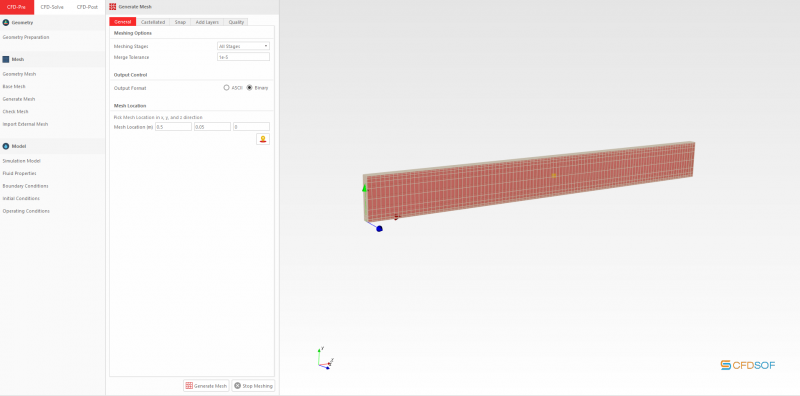
Setelah koordinat mesh dipindahkan, dilakukan Generate Mesh, sehingga box mesh akan menjadi seperti yang terlihat berikut.
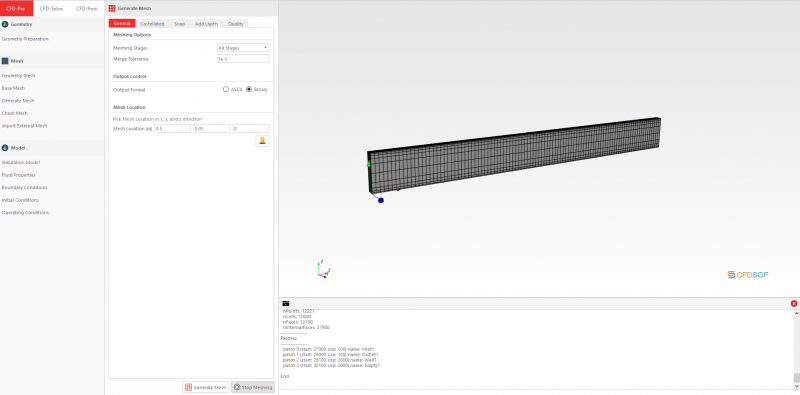
Kemudian dilakukan opsi Check Mesh.
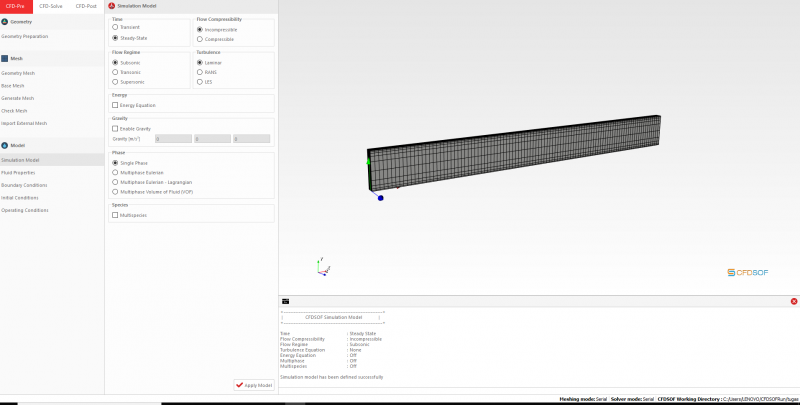
Masuk ke opsi Simulation Model, karena simulasi kali ini adalah Fluida Inkompresibel dan Steady-State (kesimpulan Steady-State di dapatkan dari hasil penghitungan Reynold Number pada studi kasus yang sebelumnya sudah diberikan), maka untuk menu-menu pada opsi Simulation Model ini tidak perlu diubah (namun jika ada perubahan, semisal fluida adalah Kompresibel, atau transien, atau ingin dilakukan penghitungan heat transfer, maka pilihan pada menu-menu tersebut dapat disesuaikan).
Pada bagian Fluid Properties, disini karena fluida yang akan ditinjau sudah sesuai (yakni Udara) maka tidak perlu dilakukan perubahan apa-apa. Namun jika ternyata fluida yang akan disimulasikan berbeda, dapat dilakukan perubahan yang sesuai.
Dalam opsi Boundary Conditions, dilakukan penyesuaian BC untuk masing-masing titiknya. Pada X- inlet, dispesifikasikan BC adalah Velocity Inlet dan menginput nilai kecepatannya serta membatasi lebih lanjut dengan tipe Surface Normal Fixed Value. Untuk X+, Y-, Y+ dilakukan penyesuaian.
Setelah itu, masuk ke opsi CFD Solve. Disini karena pada bagian Numerical Schemes tidak perlu dilakukan penyesuaian apapun, langsung masuk ke Run Solver. Pada bagian ini, perlu diperhatikan untuk megganti tipe Write Control menjadi Run Type sebanyak 1000 kali (dipilih 1000 karena menyamakan dengan jumlah iterasi pada Steady-State Simulation Time Control. Lalu, klik tombol Run Solver. Akan didapatkan hasil bahwa simulasi ini konvergen setelah 154 kali iterasi.
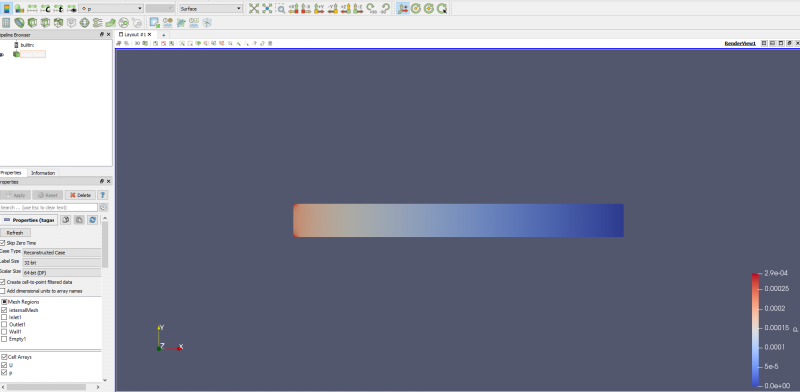
Berlanjut ke opsi CFDPost, pilih post processing with third party tools. Ini akan membawa kita ke software untuk memvisualisasi hasil simulasi, Paraview. Pada Paraview, setelah di klik apply pada file dari CFDSOF tadi, akan muncul hasil visualisasi sebaran pressure pada simulasi.
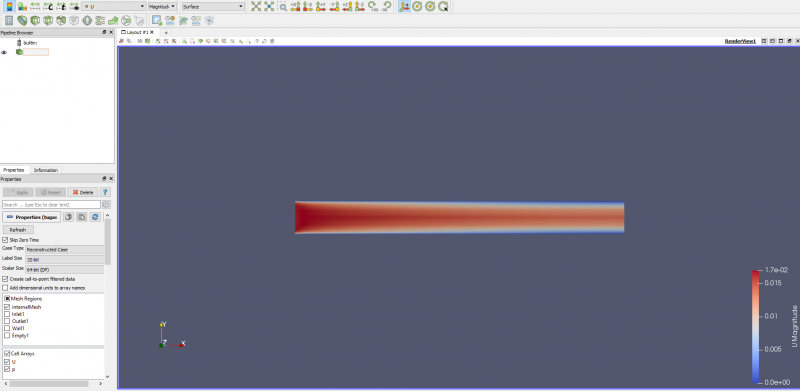
Dapat diganti menjadi hasil sebaran kecepatan fluida sebagai berikut.
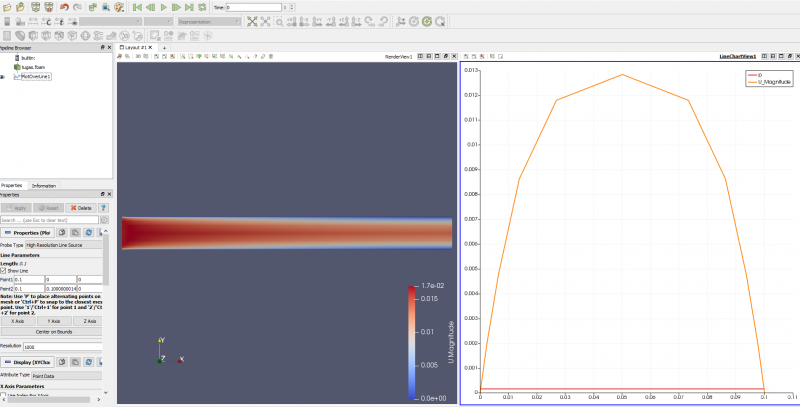
Untuk mendapatkan grafiknya, dapat dipilih opsi Outline Over Line dan kemudian memilih Y axis pada panel kiri. Untuk line parameters X point 1 dan point 2 dipilih 0.1 . Klik apply dan akan muncul grafik seperti demikian.
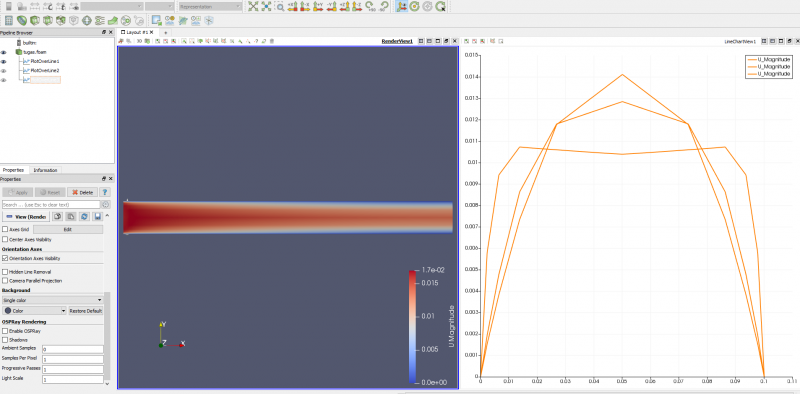
Proses Outline Over Line saya ulangi dua kali lagi dengan point 1 dan point 2 berikutnya adalah 0.5, 0,5 dan 1, 1. Hasil perbandingan grafiknya adalah sebagai berikut.
DESKRIPSI
Entrance Region
Merupakan jarak yang dilalui aliran setelah memasuki pipa sebelum aliran berkembang sepenuhnya.
Fully Developed Flow
Mengimplikasikan bahwa profil kecepatan suatu fluida tidak berubah pada arah aliran fluida, sehingga menyebabkan momentum juga tidak berubah pada arah fluida. Dalam kasus ini, tekanan pada arah ini akan sama besar (mengimbangi) gaya geser di dekat dinding.
Entrance Length
Mengacu pada panjang dari Entrace Region, suatu area yang mengikuti jalur masuk pipa dimana efek dari dinding interior berpengaruh pada aliran sebagai boundary layer yang meluas.
PERTEMUAN II MEKANIKA FLUIDA (Rabu, 04/01/2020)
Pada pertemuan hari ini (04/01/2020), pak Dai memberikan kuliah mengenai tiga hukum dasar yang digunakan pada mekanika fluida. Yakni ; konservasi energi, konservasi massa, dan konservasi momentum.
Kemudian juga dibahas tentang entrance region, fully developed flow, pressure drop dan tekanan-tekanan.
1. Entrance region; jarak fluida dari saluran masuk hingga profil aliran tidak berubah.
2. Fully developed flow ; daerah setelah aliran masuk saat kecepatannya tetap.
3. Pressure Drop ; perbedaan tekanan (dalam hal ini tekanan dinamik).
4. Tekanan ; pada dasarnya adalah energi, sedangkan energi tidak dapat hilang atau dibentuk, dalam artian pressure drop sendiri bukanlah perbedaan tekanan yang hilang, namun energi dalam bentuk tekanan tersebut berubah menjadi energi panas dikarenakan gesekan dengan dinding aliran.
Kemudian setelah pak Dai memberikan materi, bang Edo memberikan simulasi CFD terkait fungsi grid yang mana akan berpengaruh pada grafik yang ditampilkan. Semakin kecil grid maka
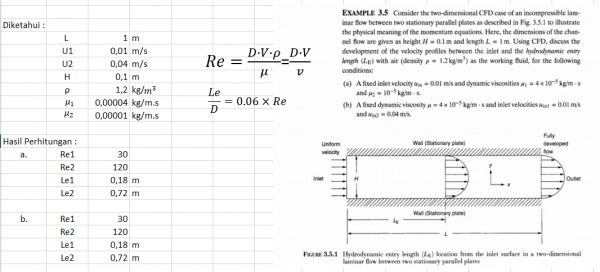
Pada pertemuan ini pak Dai memberikan PR yang dikerjakan dengan software CFDSOF untuk mencari perubahan kecepatan pada entrance region. Berikut adalah Persoalan dan data-data yang diperoleh :
Pada umumnya bentuk vektor kecepatan searah sumbu x yang terjadi pada persoalan diatas adalah sebagai berikut:
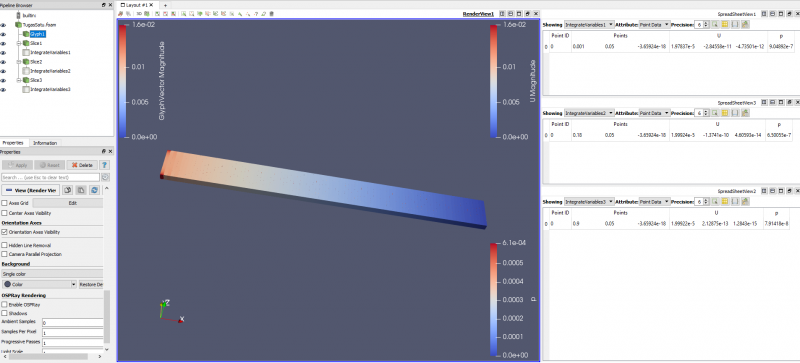
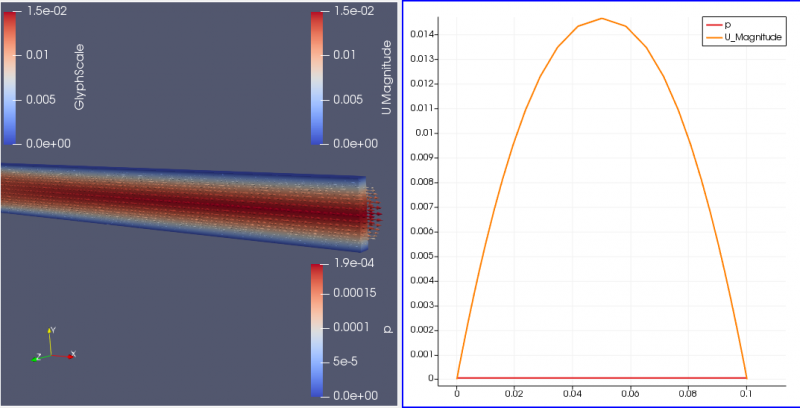
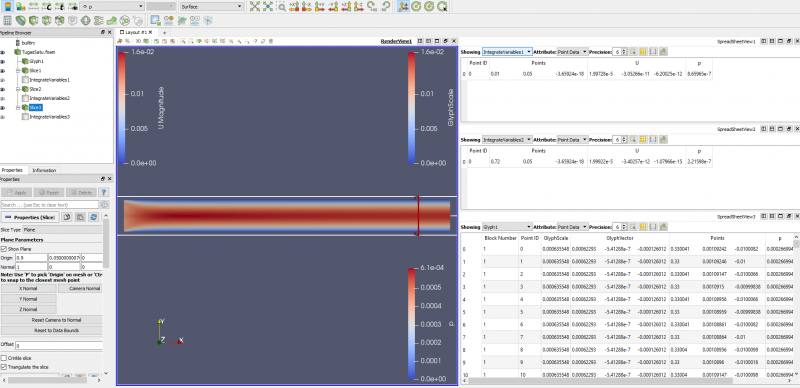
Pada point a bagian 1 berdasarkan data-data yang ada dengan inlet velocity adalah 0,01 m/s dengan viskositas dinamik 0,00004 kg/m.s diperoleh Reynold numbers sebesar 30 dan entrance length adalah 0,18 m. Berikut adalah hasil grafik kecepatan dan tekanan yang diperoleh :
Kemudian titik searah sumbu x yang digunakan untuk mengetahui perubahan kecepatan yang diperoleh adalah 0,01 m, 0,18 m(entrance length), 0,5 m dan 0,9 m adalah sebagai berikut :
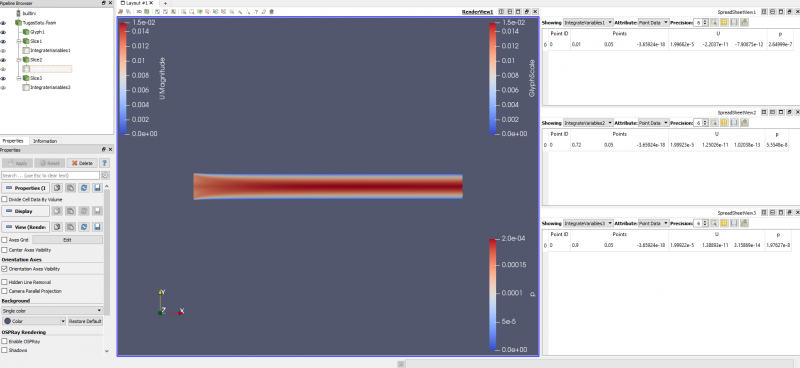
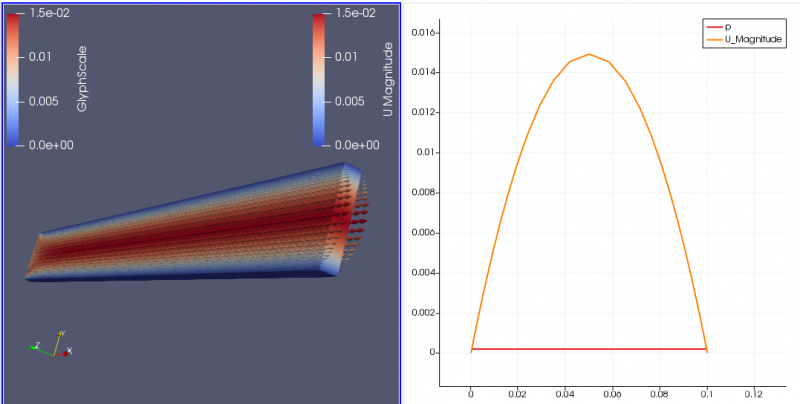
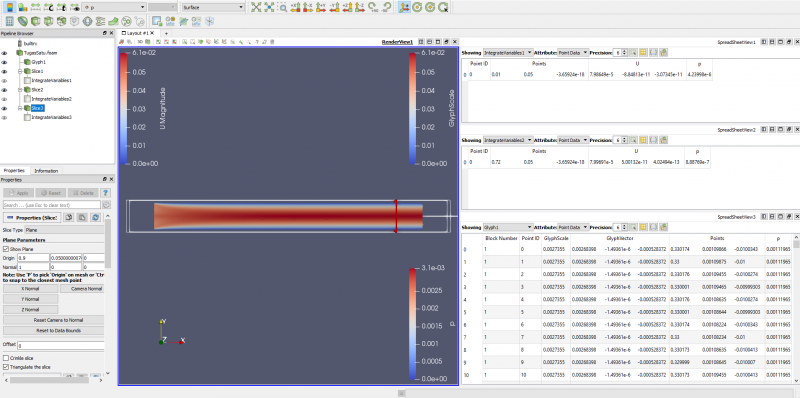
Pada poin a bagian 2 berdasarkan data-data yang ada dengan inlet velocity adalah 0,01 m/s dengan viskositas dinamik 0,00001 kg/m.s diperoleh Reynold numbers sebesar 120 dan entrance length adalah 0,72 m. Berikut adalah hasil grafik kecepatan dan tekanan yang diperoleh :
Kemudian titik searah sumbu x yang digunakan untuk mengetahui perubahan kecepatan yang diperoleh adalah 0,01 m, 0,72 m(entrance length), 0,8 m dan 0,99 m adalah sebagai berikut :
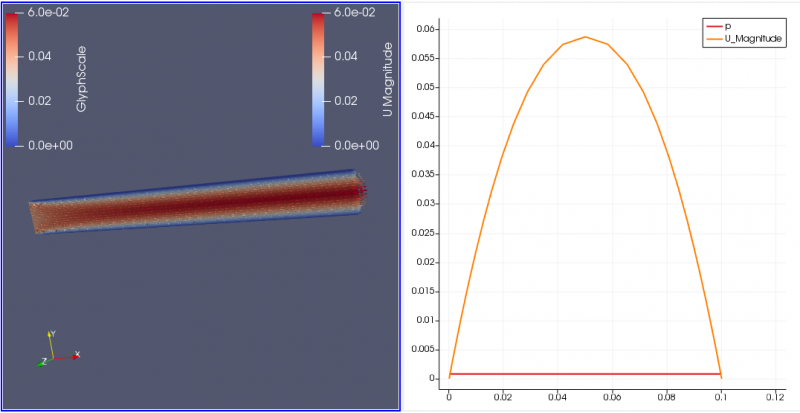
Dari hasil simulasi CFDSOF yang disupport oleh software paraview pada point a bagian 1 dan 2, perubahan kecepatan pada entrance region lebih besar jika dibandingkan dengan perubahan kecepatan setelah entrance region yang mana perubahan kecepatan jauh lebih kecil. Hal ini menguatkan teori bahwa perhitungan kecepatan pada daerah entrance region jauh lebih kompleks daripada perubahan kecepatan pada fully developed region yang mana perubahan kecepatan sangat kecil sehingga perhitungannya pun jauh lebih simpel.
Pada point b bagian 1 berdasarkan data-data yang ada dengan inlet velocity adalah 0,01 m/s dengan viskositas dinamik 0,00004 kg/m.s diperoleh Reynold numbers sebesar 30 dan entrance length adalah 0,18 m. Berikut adalah hasil grafik kecepatan dan tekanan yang diperoleh :
Kemudian titik searah sumbu x yang digunakan untuk mengetahui perubahan kecepatan yang diperoleh adalah 0,01 m, 0,18 m(entrance length), 0,5 m dan 0,9 m adalah sebagai berikut :
Pada poin b bagian 2 berdasarkan data-data yang ada dengan inlet velocity adalah 0,04 m/s dengan viskositas dinamik 0,00004 kg/m.s diperoleh Reynold numbers sebesar 120 dan entrance length adalah 0,72 m. Berikut adalah hasil grafik kecepatan dan tekanan yang diperoleh :
Kemudian titik searah sumbu x yang digunakan untuk mengetahui perubahan kecepatan yang diperoleh adalah 0,01 m, 0,72 m(entrance length) dan 0,9 m adalah sebagai berikut :
Dari hasil simulasi CFDSOF yang disupport oleh software paraview pada point b bagian 1 dan 2, perubahan kecepatan pada entrance region lebih besar jika dibandingkan dengan perubahan kecepatan setelah entrance region yang mana perubahan kecepatan jauh lebih kecil. Hal ini menguatkan teori bahwa perhitungan kecepatan pada daerah entrance region jauh lebih kompleks daripada perubahan kecepatan pada fully developed region yang mana perubahan kecepatan sangat kecil sehingga perhitungannya pun jauh lebih simpel.
Pada poin a dan b, seiring dengan perubahan kecepatan pada entrance region, parameter lain yang berubah adalah tekanan dinamik dikarenakan hubungan tekanan dinamik dan kecepatan adalah sebagai berikut :
Dengan μ dan V berturut-turut adalah viskositas dinamik dan kecepatan. Hal ini menyebabkan tekanan dinamik cenderung lebih konstan ketika berada pada fully developed region dikarenakan perubahan kecepatan pada daerah tersebut sangat kecil, namun sebaliknya tekanan dinamik cenderung mengalami perubahan yang cukup besar ketika berada pada entrance region.
PERTEMUAN III MEKANIKA FLUIDA (Selasa, 04/07/2020)
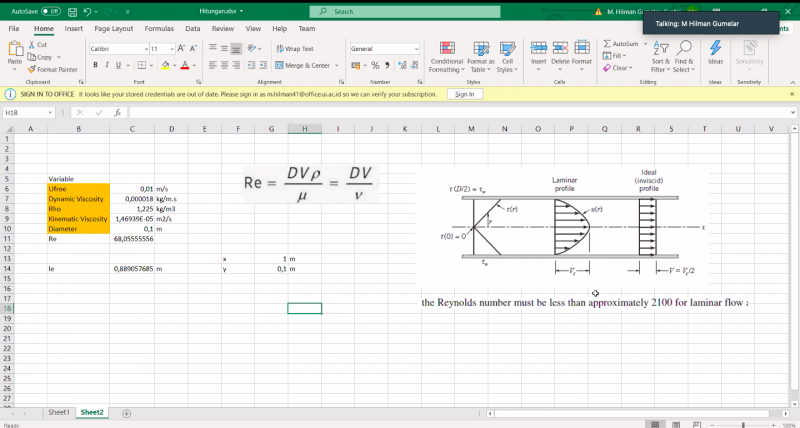
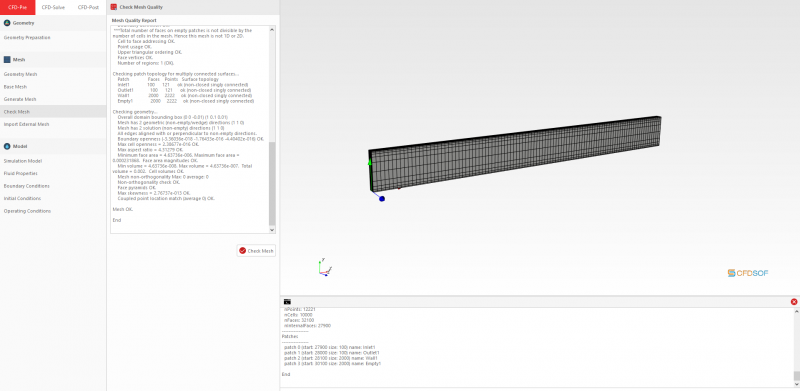
Pada pertemuan ini dijelaskan mengenai governing equation untuk aliran fluida. Sebagai medium penjelasannya, digunakanlah soal berikut ;
Dari soal tersebut, dapat dijelaskan bahwa penggunaan governing equation, pada kasus ini adalah Navier-Stokes, dapat dimodifikasi sesuai dengan kondisi pada soal. Navier-stokes dapat diterapkan pada dua dimensi (seperti pada soal) dan dalam kondisi velocity profile seperti apapun.
Selain membahas mengenai governing equation , pada pertemuan ini juga dibahas mengenai hubungan Reynolds Number dengan Gaya Inersia dan Friction Force. dijelaskan bahwa, semakin tinggi gaya inersia, akan semakin tinggi pula tendensi terjadinya perubahan jenis aliran dari laminer ke turbulen. Hal ini disebabkan karena semkain naiknya nilai inersia, akan berpengaruh kepada terjadinya Eddy pada aliran (atau bisa juga disebut sebagai olakan. Olakan-olakan ini akan mengubah aliran laminer yang teratur menjadi aliran turbulen yang bentuknya acak dan cenderung memiliki vortex.
Disebutkan pula bahwa viskositas memiliki hubungan dengan tegangan geser. Semakin tinggi viskositas, entrance length akan semakin pendek atau semakin dekat dengan hulu aliran. Hal ini disebabkan karena, semakin kental (yang berarti semakin tinggi viskositasnya) suatu fluida, alirannya akan sulit untuk memiliki olakan ataupun vortex. Karena, dengan semakin tingginya viskositas, friction force akan semakin tinggi pula yang akan meningkatkan tegangan geser antar lapisan fluidanya.
PERTEMUAN IV MEKANIKA FLUIDA (Rabu, 04/08/2020)
Pada kesempatan ini dijelaskan lebih lanjut mengenai macam-macam aliran fluida berdasarkan reynolds numbernya. Terdapat tiga jenis fluida yang bisa dibagi berdasarkan nilai Re. Yakni ;
1. Laminar Flow ; nilai Re untuk laminar flow adalah kurang lebih dibawah 1400. Aliran laminar ini memiliki karakteristik yang dikenal sebagai fluida yang ideal dan dapat dikatakan sebagai fluida yang memiliki losses paling sedikit.
2. Transition Flow ; untuk fluida yang memiliki Re antara 1400 hingga 4000, dinamakan aliran transisi. Disebut demikian karena aliran ini masih memiliki karakteristik dari laminar flow dan sudah memiliki elemen-elemen karakteristik dari turbulent flow.
3. Turbulent Flow ; Fluida dengan Re diatas 4000 dikategorikan sebagai turbulent flow. Meskipun flow ini dianggap sebagai aliran yang tidak ideal, ini adalah aliran yang sesungguhnya berada pada dunia nyata. Aliran ini bersifat unsteady, complex, dan three-dimensional sehingga untuk melakukan analisis terhadap aliran ini, diperlukan konsep dan komputasi yang lebih rumit jika dibandingkan dengan laminar flow yang bisa menggunakan asumsi untuk fluida Bernoulli.
Selain ini, dijelaskan juga bahwa terdapat bermacam-macam kecepatan pada turbulent flow serta karakteristik dari turbulent flow itu sendiri. Dibahas juga mengenai apa-apa saja yang perlu diperhatikan pada turbulent flow dan faktor apa yang memengaruhi pressure drop pada aliran turbulen.
Dilakukan pula simulasi CFD untuk aliran turbulen dan ditunjukkan perbedaan velocity profile pada aliran turbulen dan laminar sebagai berikut ;
PERTEMUAN V MEKANIKA FLUIDA (Selasa, 04/14/2020)
Pada kesempatan ini, diminta untuk membuat artikel dengan referensi yang mengacu pada Soal-jawab Mekanika Fluida untuk nomor 1 hingga 6. Artikel tersebut terlampir sebagai berikut ;
QUIZ 1
ARTIKEL I ; Penggunaan Navier-Stokes untuk Aliran Laminer 2 Dimensi
Dalam kasus dimana kecepatan vertikal (v) sama dengan nol dan komponen kecepatan horizontal (u) bergantung terhadap x, dapat dikatakan bahwa komponen u adalah fungsi dari y.
Hal ini dapat di buktikan dengan menggunakan rumus kontinuitas dari persamaan Navier-Stokes untuk aliran dua dimensi;
Du/dx + dv/dy = 0 Du/dx + 0 = 0 Du/dx = 0
Kemudian, dengan menggunakan kondisi ini pada rumus momentum x, diketahui bahwa
D2u/dy2 = 1/μ dp/dx
Dapat disimpulkan bahwa ketentuan untuk kekalan momentum pada kasus ini adalah persamaan gaya shear dan pressure.
Dengan menggunakan dua kali integral, di dapatkan kecepatan horizontal u terhadap y ;
U(y) = 1/2μ (dp/dx) y2 + C1y + C2
Dan kondisi batas untuk menentukan C1 serta C2 adalah ;
U = 0 untuk y = H/2 (no slip)
Du/dy = 0 untuk y = 0 (simetris)
Untuk kondisi simetris, didapatkan C1 = 0.
Maksud dari kondisi no slip disini adalah fluida dianggap sebagai fluida viskos. Diasumsikan bahwa pada solid boundary, fluida akan memilii kecepatan 0 terhadap dinding pipa.
Menggunakan metode subtitusi, akan di dapatkan nilai C2 = -1/2μ (dp/dx) (H/2)2.
Dengannya profil kecepatan u(y) akan menjadi ;
U (y) = 3/2 H2/12μ (-dp/dx) (1-(y2/(H/2)2)
Gradien kecepatan dp/dx disini bernilai negatif karena pressure berkurang disepanjang aliran. Hal ini disebabkan karena adanya pressure drop.
Untuk aplikasinya, soal ini dapat digunakan sebagai kasus simulasi untuk aliran air pada pipa secara dua dimensi.
ARTIKEL II ; Pengaruh Viskositas dan Kecepatan Inlet pada Entrance Length Aliran Laminer
Pada kasus ini dapat dilihat setelah dilakukan perhitungan bahwa, baik untuk kasus A dimana kecepatan inlet dipertahankan dan viskositas diubah (ada dua jenis), maupun kasus B dimana viskositas dipertahankan dan kecepatan inlet diubah (ada dua jenis),
keduanya akan memberikan dua hasil entrance length yang sama dan secara tidak langsung, memberikan Reynold’s number yang sama (maksudnya, hanya akan ada dua nilai LE berbeda untuk empat kondisi ini).
Hal ini disebabkan karena, LE sebanding dengan Re. Maka perubahan yang terjadi pada Re akan menyebabkan perubahan secara proporsional pada LE.
Kasus dengan Re dan LE ini juga berpengaruh terhadap velocity profile nya.
Pada bagian A, kasus pertama, dimana kecepatan inlet adalah 0.01 m/s dan viskositas dinamik = 4 x 10-5 kg/m.s memiliki profil kecepatan yang berbeda saat viskositas dinamiknya diubah menjadi 10-5 kg/m.s
Hal ini disebabkan karena pada saat kedua kondisi tersebut diberikan gaya inersia yang sama, fluida dengan viskositas dinamik yang lebih tinggi akan memberikan gaya friksi yang lebih besar, sehingga menghasilkan momentum fluida.
Mengakibatkan terbentuknya kondisi fully developed dengan lebih cepat.
Mengapa? Karena, aliran fluida lebih pelan dan stabil jika dibanidngkan dengan fluida yang memiliki viskositas dinamik lebih kecil (yang akan memiliki LE lebih panjang).
Untuk bagian B, hal serupa terjadi. Yang menjadi perhatian adalah bagaimana fluida dengan viskositas dinamik yang sama namun memiliki kecepatan inlet berbeda, akan memberikan hasil yang serupa dengan kasus A (dimana kecepatan inlet sama dan viskositas dinamik berbeda).
Ini dapat dijelaskan dengan menggunakan persamaan Navier-Stokes untuk aliran dua dimensi ;
Inersia = -pressure + friksi
Yang mana, gaya inersia sebanding dengan gaya friksi (dan gaya inersia sebanding dengan kecepatan).
Aplikasi untuk kasus ini akan berguna untuk membuat simulasi mengenai berapa pressure drop serta sejauh apa fluida baru akan stabil dalam beberapa kondisi tertentu.
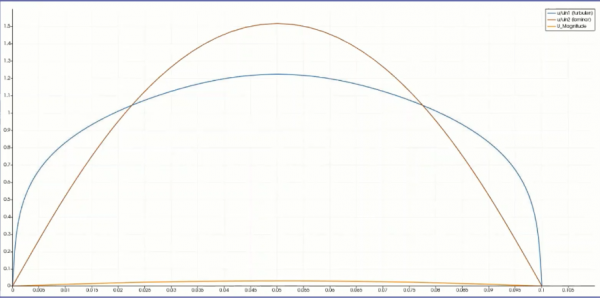
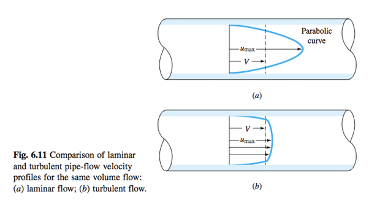
ARTIKEL III ; Karakter Profil Kecepatan Laminer vs Turbulen
Pada kasus ini, terlihat dengan jelas perbedaan profil kecepatan laminer dan turbulen.
Pada aliran laminer, profil kecepatan berbentuk parabola, sedangkan untuk aliran turbulen, pada area fully developed , profil kecepatan cenderung berbentuk datar.
Hal ini disebabkan karena viskositas turbulen yang tinggi berdifusi ke aliran. Atau dapat juga dijelaskan bahwa akibat dari nilai Reynolds number yang tinggi,
distribusi pada aliran turbulen terjadi secara acak. Yang disebabkan karena adanya tegangan geser yang besar.
Tegangan geser ini menjadi parameter yang cukup penting untuk mencari distribusi kecepatan pada aliran turbulen karena, akan adanya ‘energi yang tertinggal’ di dinding. Energi yang tertinggal ini akan menyebabkan persebaran kecepatan pada aliran turbulen akan cenderung datar.
ARTIKEL IV ; Pengaruh Sudut Elevasi pada Pipeline untuk Aliran Laminer
Dalam perancangan suatu pipeline tentu pressure drop menjadi salah satu parameter vital yang harus dikonsiderasi untuk menentukan bentuk isometrik pipeline.
Rugi-rugi tekanan yang terlalu besar akan menyebabkan fluida tidak dapat mengalir hingga ke tujuannya tanpa bantuan dari pompa.
Hal yang perlu diperhatikan dalam pressure drop adalah bahwa untuk suatu kondisi fluida yang sama, apabila sudut elevasi pipeline berubah,
maka pressure drop yang didapatkan tidak akan sama.
Untuk memberikan suatu bukti akan klaim ini, dimisalkan suatu fluida dengan aliran laminer yang berada pada dua kondisi.
Kondisi pertama adalah fluida mengalir pada pipeline yang lurus horizontal. Sedangkan kondisi kedua, fluida mengalir pada pipeline yang memiliki sudut elevasi θ.
Pada dua kondisi ini, fluida memiliki viskositas, massa jenis, dan flowrate yang sama.
Dalam hukum Poiseulle, dinyatakan bahwa untuk flowrate, viskositas, dan massa jenis yang sama, pressure drop akan dikurangi oleh gamma dikali panjang dikali sinus dari sudut elevasi. Sehingga, pada kondisi pipa horizontal pressure drop yang didapatkan akan lebih kecil jika dibandingkan dengan pada kondisi pipa menanjak (memiliki sudut elevasi).
Perlu diperhatikan, jika pipeline berada pada kondisi turunan, gravitasi akan membantu pergerakan fluida, sehingga pressure drop yang lebih kecil akan di dapatkan (sin θ < 0) . Jika pipeline berada pada kondisi menanjak, pressure drop yang didapatkan akan lebih besar (sin θ > 0).
Dengan penjelasan demikian, maka terlihat bahwa untuk perancangan pipeline di lapangan sangat di pengaruhi oleh sudut elevasi.
Sehingga setelah dilakukan kalkulasi, akan diketahui di titik-titik mana saja akan diperlukan pompa untuk mengatasi pressure drop yang terjadi.
Aplikasi di lapangan untuk ini ada pada perancangan pipeline migas.
ARTIKEL V ; Turbulen dan Pengaruhnya pada Aliran
Terdapat dua jenis aliran. Yakni laminer dan turbulen. Pada kehidupan sehari-hari, jenis aliran turbulen akan lebih umum ditemui dibanding laminer.
Yang khas dari aliran turbulen adalah karakteristiknya yang cenderung acak. Hal ini terjadi baik pada kecepatan, pressure, shear stress, temperatur,
dan variabel-variabel lain yang memiliki medan.
Selain itu, aliran turbulen di sebabkan oleh vorticity 3 dimensi yang juga bergerak acak. Vorticity adalah perputaran partikel fluida.
Dapat di highlight pula, bahwa pada aliran turbulen, shear stress dan pressure drop akan jauh lebih tajam dibanding dengan aliran laminer. Hal ini disebabkan karena sublayer viskos pada aliran turbulen sangat tipis. Kondisi ini menyebabkan ketidak sempurnaan dari dinding pipa akan masuk ke sublayer dan memengaruhi karakteristik aliran.
Viskos sub layer adalah lapisan tipis dekat dinding yg kontak langsung dengan dinding aliran fluida pd aliran turbulen dgn turbulensi minimal yg nantinya energi turbulen itu diubah mnjadi energi panas.
Aliran turbulen fully developed pada pipa juga merupakan aliran axisymmetric. Yang berarti pola aliran identik pada setiap bidang yang melewati suatu garis lurus.
ARTIKEL VI ; Rugi-rugi Tekanan pada Laminer dan Turbulen
Sering disebutkan bahwa aliran laminer merupakan aliran fluida yang dianggap ideal. Sedangkan aliran turbulen adalah aliran non-ideal yang banyak ditemui di kehidupan sehari-hari.
Aliran laminer dianggap sebagai aliran fluida ideal, salah satu nya adalah karena pressure drop atau rugi-rugi tekanan yang terjadi pada aliran ini sangat kecil.
Untuk suatu kondisi yang sama, rugi-rugi tekanan pada aliran turbulen dapat meningkat tajam jika dibandingkan dengan laminer.
Hal ini disebabkan karena adanya pengaruh dari friction force yang terjadi. Pada aliran turbulen, nilai friction force ini sangat besar disebabkan oleh karakteristik aliran tersebut yang cenderung acak.
Semakin meningkatnya friction force, maka rugi-rugi tekanan yang didapatkan akan semakin besar.
Dengan penjelasan tersebut, pada kehidupan sehari-hari, sudah menjadi hal yang umum untuk membuat aliran mendekati kondisi laminer (sedekat yang dimungkinkan) salah satunya adalah untuk menekan terjadinya rugi-rugi tekanan yang terlalu tinggi.