Sahdha Prakasa

Tugas Metode Numerik 1

Dalam menimba ilmu, tahap yang paling sempurna adalah mempelajari fundamental atau dasar dari ilmu tersebut. Untuk apa kegunaannya, bagaimana pengaplikasiannya, dan bagaimana kita bisa mempelajarinya. Dengan mempelajari hal - hal yang dimulai dari pertanyaan dasar maka kita akan benar - benar memahami ilmu tersebut bahkan akan bermanfaat bagi diri kita maupun orang lain.

Di sisi lain, bermanfaat atau tidaknya suatu ilmu lebih bergantung pada manusianya, di sini lah akal manusia bekerja sebagaimana fungsinya. Apakah ilmu yang didapat menjadikannya manfaat bagi diri dan orang lain, atau bahkan digunakan untuk kejahatan yang bersifat menguntungkan diri sendiri namum merugikan orang lain ?

Manusia berakal adalah syarat untuk mengikuti mata kuliah Metode Numerik ini, begitulah pesan yang dikutip Dr. Ahmad Indra atau dipanggil Aki DAI, pengajar perkuliahan Metode Numerik. Beliau berpesan kita sebagai manusia harus mengenal siapa dirinya sendiri, hal ini hanya dapat dilakukan sebagai makhluk yang berakal, dengan memahami dan mengenal diri sendiri kita tahu kelebihan, potensi, dan kekurangan dalam diri kira sehingga kita terus berlajar untuk memperbaiki kekurangan diri dan menjadi manusia yang lebih baik serta berguna bagi sesama.

Adapun bentuk aplikasi dari mata kuliah Metode Numerik ini, diantaranya proses pemrograman dasar seperti algoritma, flowchart, metode iterative. Penyelesaian persamaan matematik seperti persamaan aljabar simultan, diferensial dan integral dapat diselesaikan, hingga penyelesaian proses optimasi ( suatu proses untuk mencapai hasil yang ideal ).Tidak hanya untuk menyelesaikan suatu persamaan, bahkan ilmu Metode Numerik ini bisa digunakan untuk menghitung distribusi pembebanan pada suatu benda dengan metode Finite Element serta menghitung tegangan / stress pada pembebanan. Sedangkan untuk referensinya,yang dijadikan referensi utama adalah buku Advanced Engineering Mathematics ( Edwin Kryzig ).

Pertemuan Metode Numerik ke 2

ax + by = c px + qy = r

Buat : 1. Algoritma

      2. Flowchart 
      
      3. Solving dengan program Python

a,b,c,p,q,r = Konstanta

x,y = variabel

- Tulis persamaan

                 ax + by = c
                 px + qy = r

- Input nilai pada a,b,c,p,q,r

- Hitung dengan menggunakan numpy method

- cari penyelesaian dengan z = np.linalg.solve(x,y)

Flow chart :

1. Print ax +by = c dan px +qy=r

2. Print masukan nilai a,b,c dan p,q,r

3. Input nilai a,b,c dan p,q,r

4. Input nilai a,b dan p,q ke dalam satu matrix

5. Input nilai c dan r ke dalam matrix yang lain

6. Lakukan perhitungan dengan menggunakan numpy linear algebra = np.linalg.solve(x,y)

7. Print hasil x dan y

import numpy as np

print("linear algebra solution :)")

print("ax + by = c")

print("px + qy = r")

print("Please input the value")

a = int(input("input value of a :"))

b = int(input("input value of b :"))

c = int(input("input value of c :"))

p = int(input("input value of p :"))

q = int(input("input value of q :"))

r = int(input("input value of r :"))

Pertemuan Metode Numerik ke 3

Dalam mengerjakan persamaan bervariabel, untuk mencari variabel tersebut ( x, y ) kita dapat menyusun konsep dan pola terlebih dahulu dengan menggunakan metode matrix

Contoh :

ax + by = c px + qy = r

[(a,b),(p,q)] [ x,y ] = [ c.r ]

contoh bahasa pemograman python

for k in range(0,n-1): for i in range(k+1,n):

if a[i,k] != 0.0: lam = a[i,k]/a[k,k] a[i,k+1:n] = a[i,k+1:n] - lam*a[k,k+1:n] b[i] = b[i] - lam*b[k]

Tugas 3

Menjelaskan setiap tahap dari pemograman pada penyelesaian persamaan di Python

Inti dari metode ini adalah membawa persamaan kedalam bentuk matriks dan menyederhanakan matriks menjadi bentuk segitiga atas. Setelah mendapat bentuk matriks tersebut dilakukan subtitusi balik untuk mendapat nilai dari akar persamaan. Namun modern ini penyelesaian dapat diakuakan dengan cepat melalui aplikasi python dengan menggunakan rumus

keterangan:

n = jumlah baris atau kolom

i = baris ke

j = kolom

k = pivot

Langkah pengerjaan:

1. Masukkan Metode numpy dengan cara "import numpy as np".

2. Masukkan def gaussElimin(a,b): dimana def itu merupakan suatu fungsi, dan fungsi tersebut adalah eliminasi gauss dengan parameter a dan b. Baris berikutnya merupakan definisi dari n, di mana n tersebut adalah len(b) yang merupakan fungsi untuk mengembalikan angka atau objek berikut masuk ke fase eliminasi. hal yang pertama dimasukkan adalah fungsi range. Fungsi range ini berfungsi untuk menampilkan suatu list data, seperti yang dilihat untuk k range nya adalah (0,n-1)

3. Masukkan fungsi range untuk i dimana fungsi tersebut parameternya adalah (k+1,n) dimana dapat ditranslate sesudah kita mengetahui nilai k yang ingin dimasukkan. Dilanjutkan dengan memasukkan fungsi if dimana, if yaitu bila suatu kondisi tertentu tercapai maka apa yang harus dilakukan. Dengan fungsi ini kita bisa menjalankan suatu perintah dalam kondisi tertentu. Dimana perintah tersebut disini adalah a[i,k ]  !=0.0: . setelah itu dilanjutkan dengan perhitungan lam dan perhitungan lainnya

4. Dilakukan fase substitusi balik, sehingga mendapatkan hasil sebagai

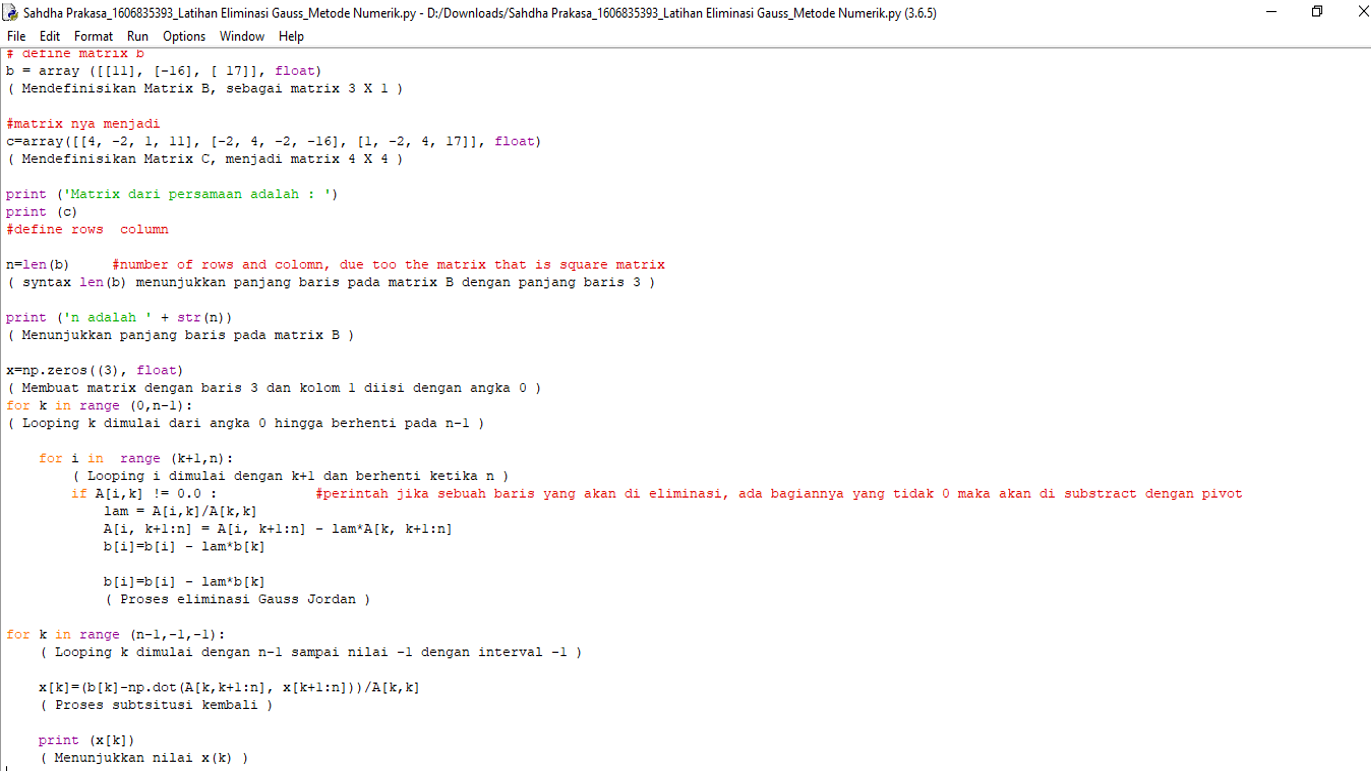
Contoh pada Latihan Eliminasi Gauss