Difference between revisions of "Cornelius"
| Line 72: | Line 72: | ||
== Elimination Gauss == | == Elimination Gauss == | ||
Ini adalah metode lain dalam penyelesaian pertidaksamaan linear. Berikut adalah hasil coding untuk penyelesaian menggunakan elimination gauss: | Ini adalah metode lain dalam penyelesaian pertidaksamaan linear. Berikut adalah hasil coding untuk penyelesaian menggunakan elimination gauss: | ||
| − | import numpy as np | + | line 1 :import numpy as np |
| − | from numpy import array | + | line 2 :from numpy import array |
| − | # define the matrix [A] | + | line 3 : # define the matrix [A] |
| − | A=array([[ | + | line 4 : A=array([[5, -4, 5], [-3, 3, -5], [6, -7, 1]], float) |
| − | # define matrix b | + | line 5 : # define matrix b |
| − | b = array ([[ | + | line 6 : b = array ([[9], [-1], [ 13]], float) |
| − | # matrix nya menjadi | + | line 7 : #matrix nya menjadi |
| − | c=array([[ | + | line 8 : c=array([[5, -4, 5, 9], [-3, 3, -5, -1], [6, -7, 1, 13]], float) |
| − | print ('Matrix dari persamaan adalah : ') | + | line 9 : print ('Matrix dari persamaan adalah : ') |
| − | print (c) | + | line 10 : print (c) |
| − | #define rows column | + | line 11 : #define rows column |
| − | n=len(b) #number of rows and colomn, due too the matrix that is square matrix | + | line 12 : n=len(b) #number of rows and colomn, due too the matrix that is square matrix |
| − | print ('n adalah ' + str(n)) | + | line 13 : print ('n adalah ' + str(n)) |
| − | x=np.zeros((3), float) | + | line 14 : x=np.zeros((3), float) |
| − | for k in range (0,n-1): | + | line 15 : for k in range (0,n-1): |
| − | + | line 16 : for i in range (k+1,n): | |
| − | + | line 17 : if A[i,k] != 0.0 : #perintah jika sebuah baris yang akan di eliminasi, ada bagiannya yang tidak 0, maka akan di substract dengan pivot | |
| − | + | line 18 : lam = A[i,k]/A[k,k] | |
| − | + | line 19 : A[i, k+1:n] = A[i, k+1:n] - lam*A[k, k+1:n] | |
| − | + | line 20 : b[i]=b[i] - lam*b[k] | |
| − | for k in range (n-1,-1,-1): | + | line 21 : for k in range (n-1,-1,-1): |
| − | + | line 22 : x[k]=(b[k]-np.dot(A[k,k+1:n], x[k+1:n]))/A[k,k] | |
| − | + | line 23 : print (x[k]) | |
Ini adalah hasil dari Modul tersebut: | Ini adalah hasil dari Modul tersebut: | ||
| + | |||
| + | [[File:Eliminationn.jpg]] | ||
| + | |||
| + | Ini adalah model dari metode elimination Gauss. Sekarang saya akan mencoba menjabarkan arti beberapa line dari metode ini. Line 1 dan 2 adalah perintah untuk menerapkan numpy dalam coding ini agar mempermudah berbagai bentuk matematik digunakan dalam coding ini. Array berguna untuk membuat data yang dinginkan dituliskan dalam format matrix. Semua kalimat yang diawali dengan tanda # hanya merupakan angka yang tidak ada hubungan dengan coding secara keseluruhan. Bagian itu bisa dihiraukan dalam coding ini. Line 4 sama line 10 adalah perintah untuk memunculkan matrix. Namun, dari coding tersebut, matrix a, b, dan c tidak berhubungan. Matrix yang muncul hanya lah matrix c dari line 8 karena perintah print hanya ditujukan pada c, sedangkan nilai c tidak dipengaruhi oleh a maupun b. Line 11 hanya perintah menuliskan apa yang ada di dalamnya. Line 12 berguna untuk mengetahui jumlah data dari b. Dalam kasus ini, nilai tersebut adalah 3 karena b memiliki 3 jenis data yang berbeda. Float dalam b tidak termasuk jenis data lain karena itu berguna untuk mendefinisikan nilai angka di dalamnya memiliki nilai 0 tambahan di belakangnya. Line 11 untuk memunculkan kalimat dan string dari n. String adalah Bahasa lain dari kalimat di dalam python. Line 14 adalah perintah untuk memunculkan zero matrix. Dengan nilai 3, berarti yang muncul adalah matrix 3 x 3. Ini digunakan untuk mendefinisikan bentuk matrix yang akan dibaca oleh perintah selanjutnya dalam line 15 sampai line 23. Line 15 sampai line 23 adalah proses eliminasi bagian dari baris yang harusnya 0. Karena kita memerlukan matrix segitiga atas untuk menyelesaikan dengan metode elimination gauss. For digunakan untuk menjalankan perintah hanya ketika argumen yang ada bersifat true. Proses yang berjalan adalah pengecekan setiap angka pada segitiga bawah dalam matrix tersebut agar nilainya menjadi 0. Line 21 juga menggunakan perintah for yang berarti hanya berjalan kalua argumennya bersifat true. Range disini memiliki 3 argumen. Argumen yang ketiga adalah interval dari setiap data yang ada dalam range tersebut. Line 22 juga merupakan pembagian nilai di koordinat data yang diberikan, tetapi ada penggunaan np.dot disana. Perintah np.dot sama seperti dot product dalam aljabar linear. Kemudian diakhiri pada line 23 dengan print (x[k]). | ||
Revision as of 09:54, 27 February 2019
Contents
Metode Numerik
METODE NUMERIK adalah teknik yang digunakan untuk memformulasikan persoalan matematik sehingga dapat dipecahkan dengan operasi perhitungan/aritmetika biasa (tambah, kurang, kali, dan bagi). Itulah pengertian yang tentunya saya dapatkan dari google. Sebuah pengertian yang singkat, jelas, dan padat. Saya pun cukup tertarik mendengar apa yang akan saya pelajari pada mata kuliah kali ini. Saya tahu bawah logika saya akan terus diuji dan dipicu selama pelajaran ini, tetapi bagaimana prosesnya tentu masih belum jelas. Bagaimana prosesnya akan dimulai bergantung pada dosen saya pada mata kuliah kali ini, yaitu Dr. Ahmad Indra atau yang kerap ingin disapa Aki Dai. Sebuah introduksi yang unik dilontarkan oleh Aki Dai waktu itu. Sebuah perkenalan yang mungkin kurang berbau "metode numerik, tetapi seperti sebuah peta untuk melihat arah dari ilmu yang akan diberikan oleh Aki Dai.
Akal
Kata yang kerap ditekankan oleh Aki Dai dalam diskusi hari itu. Apa yang membedakan manusia dari semua mahkluk hidup lainnya? Akal budi. Jawaban yang sudah sering dilontarkan ini menjadi topik bahasan kali ini. Topik ini pun bukan sekadar sebuah intermezzo untuk introduksi hari itu saja. Ini dibuktikan dari tujuan perkuliahan yang ingin dicapai oleh Aki Dai. Berikut adalah Kalimat dari tujuan perkuliahan metode numerik ini :
1. Memahami konsep/prinsip dan mampu menerapkannya
2. Menjadi orang yang lebih mengenal siapa dirinya
Tujuan kedua merupakan poin yang menarik. Kenapa harus mengenal diri? Apa yang membuat kita menjadi lebih mengenal diri? Bagaimana Metode Numerik dapat memberikan kita sebuah pandangan mengenai diri kita? Menurut saya, hal yang dimaksud oleh Aki Dai adalah cara kita berpikir. Dalam diskusi hari itu, Aki Dai juga menyebutkan tujuan dan kegunaan dari kita belajar matematika dari kecil. Matematika membantu kita berpikir lebih logis dan sistematis. Pola pikir itu lah yang sebenarnya ingin ditanamkan sejak kecil. Belajar metode numerik tidak jauh berbeda tujuannya dengan matematika. Kita diharapkan bias lebih baik lagi sebagai manusia yang berakal.
Masalah Teknik
Kita kerap mencari solusi dari masalah-masalah yang ada di sekitar kita. Kita menggunakan berbagai metode untuk bisa menerapkan solusi yang paling efektif dan efisien agar masalah yang ada dapat diselesaikan secepatnya. Dari berbagai metode yang ada, beberapa orang mulai mencari cara yang universal yang dapat merepresentasikan metode penyelesaian masalah yang tepat guna. Salah satu metode yang dikembangkan adalah metode numerik.
Ini merupakan contoh dari metode penyelesaian masalah dengan menggunakan bantuan komputasi. Kita bisa membuat model matematis dari masalah yang ada. Model ini seperti bayangan yang merepresentasikan masalah yang benar-benar terjadi. Contohnya, kita bisa menghitung efisiensi dari pemakaian energi kapal dalam satu kali perjalanan. Kita sudah tidak perlu melakukan uji coba berulang-ulang untuk menemukan data yang diperlukan agar dapat mengetahui efisiensinya. Kita bisa menggunakan bantuan komputasi dengan membuat model dari permasalahn tersebut. Dengan data-data yang tepat, keakuratan model ini bisa menjamin solusi yang tepat atas masalah tersebut.
Nonlinear Equation in Python
Tugas kali ini adalah mencoba membahasakan pertidaksamaan linear dengan menggunakan Bahasa python. Pertidaksamaan yang ingin diselesaikan adalah sebagai berikut:
ax + by = c
px + qy = r
Nilai a, b, p, q adalah konstanta dengan nilai tertentu. x dan y adalah variabel yang merupakan solusi dari pertidaksamaan tersebut. Dengan menggunakan python kita harus bisa menyelesaikan masalah itu. Berikut adalah program untuk menyelesaikan pertidaksamaan linear dengan menggunakan python:
import numpy as np
print("Please input the value")
a = int(input("input value of a :"))
b = int(input("input value of b :"))
c = int(input("input value of c :"))
p = int(input("input value of p :"))
q = int(input("input value of q :"))
r = int(input("input value of r :"))
x = np.array([[a,b],[p,q]])
y = np.array([c,r])
z = np.linalg.solve(x,y)
xval = int(z[0])
yval = int(z[1])
print("x = ",xval)
print("y = ",yval)
Program python ini menggunakan numpy untuk membantu dalam membahasakan apa itu x dan y sebagai variable. Modul numpy yang digunakan adalah array untuk matriks, linalg untuk menyelesaikan permasalahan aljabar linear ini. Dengan memasukkan berbagai nilai untuk konstanta, dengan catatan nilainya adalah angka, kita akan mendapatkan nilai x dan y dari program ini.
Python
Dari contoh sebelumnya, kita dapat melihat penyelesaian masalah dengan menggunakan python. Metode-metode ini merupakan penyelesaian dari aljabar linear. Kita hanya menerjemahkannya dengan menggunakan bahasa python. Python hanya bisa mengerti tambah, kurang, kali, dan bagi. Kita harus bisa menemukan pola dalam metode penyelesaian pertidaksamaan linear. Tentu saja python tidak hanya bisa menyelesaikan permasalahan pertidaksamaan linear. Python bisa menyelesaikan berbagai permasalahan matematik, dengan catatan kita bisa menuliskannya dalam bahasa yang dimengerti oleh python. Pertidaksamaan yang sebelumnya pun bisa diselesaikan dengan berbagai metode. Metode lainnya untuk menyelesaikannya adalah dengan menggunakan elimination gauss. Contoh lainnya dalam penyelesaian masalah matematik dengan menggunakan python adalah limit. Dua contoh ini bisa dilihat dalam penjelasan selanjutnya.
Elimination Gauss
Ini adalah metode lain dalam penyelesaian pertidaksamaan linear. Berikut adalah hasil coding untuk penyelesaian menggunakan elimination gauss:
line 1 :import numpy as np line 2 :from numpy import array
line 3 : # define the matrix [A] line 4 : A=array([[5, -4, 5], [-3, 3, -5], [6, -7, 1]], float)
line 5 : # define matrix b line 6 : b = array ([[9], [-1], [ 13]], float)
line 7 : #matrix nya menjadi line 8 : c=array([[5, -4, 5, 9], [-3, 3, -5, -1], [6, -7, 1, 13]], float)
line 9 : print ('Matrix dari persamaan adalah : ')
line 10 : print (c)
line 11 : #define rows column
line 12 : n=len(b) #number of rows and colomn, due too the matrix that is square matrix
line 13 : print ('n adalah ' + str(n))
line 14 : x=np.zeros((3), float)
line 15 : for k in range (0,n-1):
line 16 : for i in range (k+1,n):
line 17 : if A[i,k] != 0.0 : #perintah jika sebuah baris yang akan di eliminasi, ada bagiannya yang tidak 0, maka akan di substract dengan pivot
line 18 : lam = A[i,k]/A[k,k]
line 19 : A[i, k+1:n] = A[i, k+1:n] - lam*A[k, k+1:n]
line 20 : b[i]=b[i] - lam*b[k]
line 21 : for k in range (n-1,-1,-1): line 22 : x[k]=(b[k]-np.dot(A[k,k+1:n], x[k+1:n]))/A[k,k] line 23 : print (x[k])
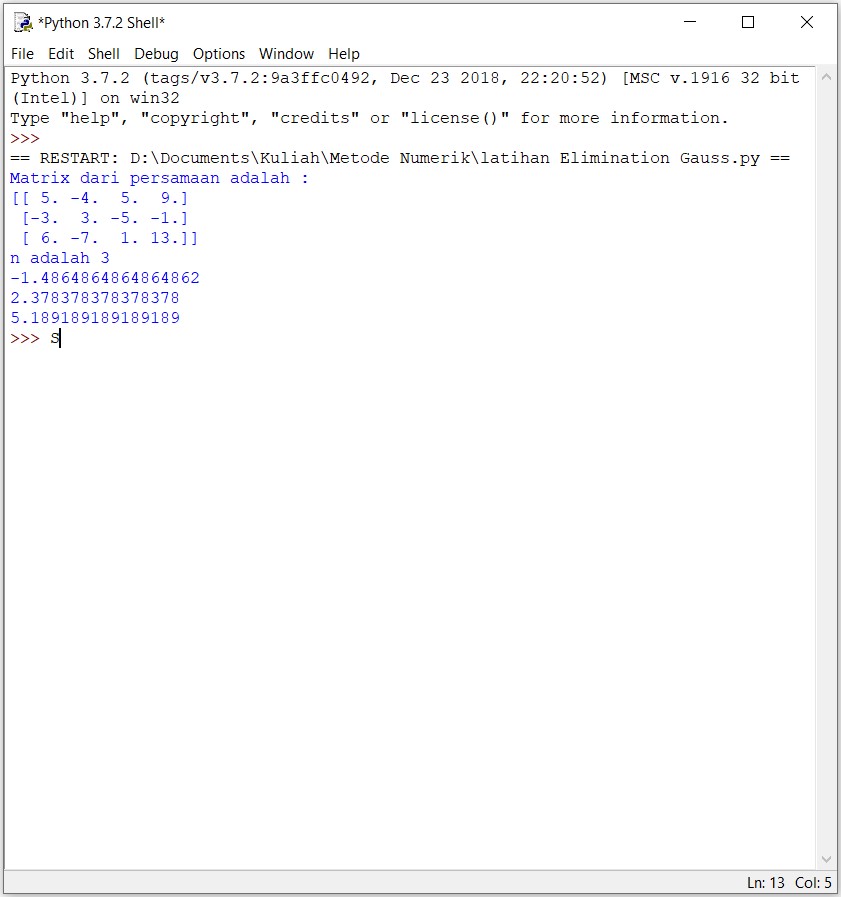
Ini adalah hasil dari Modul tersebut:
Ini adalah model dari metode elimination Gauss. Sekarang saya akan mencoba menjabarkan arti beberapa line dari metode ini. Line 1 dan 2 adalah perintah untuk menerapkan numpy dalam coding ini agar mempermudah berbagai bentuk matematik digunakan dalam coding ini. Array berguna untuk membuat data yang dinginkan dituliskan dalam format matrix. Semua kalimat yang diawali dengan tanda # hanya merupakan angka yang tidak ada hubungan dengan coding secara keseluruhan. Bagian itu bisa dihiraukan dalam coding ini. Line 4 sama line 10 adalah perintah untuk memunculkan matrix. Namun, dari coding tersebut, matrix a, b, dan c tidak berhubungan. Matrix yang muncul hanya lah matrix c dari line 8 karena perintah print hanya ditujukan pada c, sedangkan nilai c tidak dipengaruhi oleh a maupun b. Line 11 hanya perintah menuliskan apa yang ada di dalamnya. Line 12 berguna untuk mengetahui jumlah data dari b. Dalam kasus ini, nilai tersebut adalah 3 karena b memiliki 3 jenis data yang berbeda. Float dalam b tidak termasuk jenis data lain karena itu berguna untuk mendefinisikan nilai angka di dalamnya memiliki nilai 0 tambahan di belakangnya. Line 11 untuk memunculkan kalimat dan string dari n. String adalah Bahasa lain dari kalimat di dalam python. Line 14 adalah perintah untuk memunculkan zero matrix. Dengan nilai 3, berarti yang muncul adalah matrix 3 x 3. Ini digunakan untuk mendefinisikan bentuk matrix yang akan dibaca oleh perintah selanjutnya dalam line 15 sampai line 23. Line 15 sampai line 23 adalah proses eliminasi bagian dari baris yang harusnya 0. Karena kita memerlukan matrix segitiga atas untuk menyelesaikan dengan metode elimination gauss. For digunakan untuk menjalankan perintah hanya ketika argumen yang ada bersifat true. Proses yang berjalan adalah pengecekan setiap angka pada segitiga bawah dalam matrix tersebut agar nilainya menjadi 0. Line 21 juga menggunakan perintah for yang berarti hanya berjalan kalua argumennya bersifat true. Range disini memiliki 3 argumen. Argumen yang ketiga adalah interval dari setiap data yang ada dalam range tersebut. Line 22 juga merupakan pembagian nilai di koordinat data yang diberikan, tetapi ada penggunaan np.dot disana. Perintah np.dot sama seperti dot product dalam aljabar linear. Kemudian diakhiri pada line 23 dengan print (x[k]).