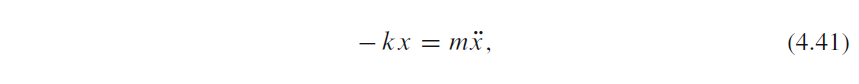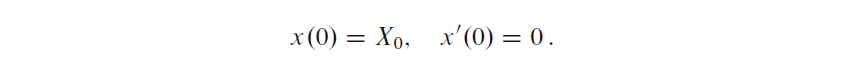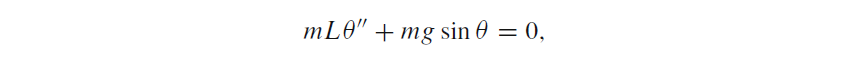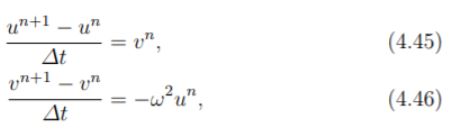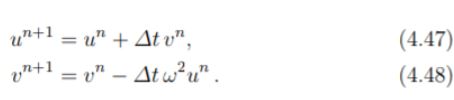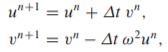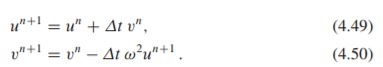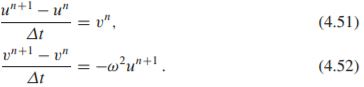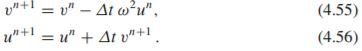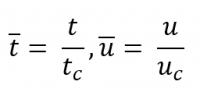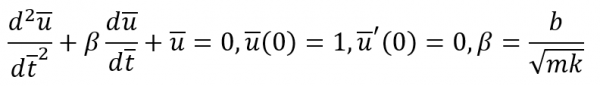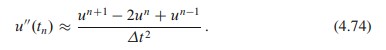Difference between revisions of "Oscillating one-dimensional systems"
Danielmeino (talk | contribs) |
|||
| Line 455: | Line 455: | ||
[[File:Kania_439-4.png|600px]] | [[File:Kania_439-4.png|600px]] | ||
| + | |||
| + | Faktnya adalah hanya ada satu parameter fisik di kasus ini: angka β. Menyelesaikan masalah ini begitu juga terkait dengan masalah utama dengan parameter yaitu m = k = Uo = 1 dan b = β. Tetapi untuk menyelsaikan masalah dengan satuan lebih umum: jika kita memdapatkan solusi ¯u(¯t;β), kita dapat menemukan solusi fisik pada kasus ini, dikarenakan : | ||
| + | |||
| + | [[File:439rumus.png|200px]] | ||
| + | |||
| + | Selama β didapat, kita dapat menemukan u untuk Uo , k, dan m dengan rumus diatas, dengan begitu pengerjaan simulasi dapat dipersingkat waktu. Ini menunjukkan pengerjaan dengan skala atau masalah satuan. | ||
| + | |||
==== 4.3.10. Ilustrasi Redaman Linier Dengan Eksitasi Sinusoidal ==== | ==== 4.3.10. Ilustrasi Redaman Linier Dengan Eksitasi Sinusoidal ==== | ||
Revision as of 21:14, 10 April 2020
Contents
- 1 Studi kasus dan Terjemahan
- 1.1 Terjemahan
- 1.1.1 4.3.1 Penurunan Model yang Sederhana
- 1.1.2 4.3.2 Solusi Numerik
- 1.1.3 4.3.3 Memprogram Metode Numerik; Kasus Khusus
- 1.1.4 4.3.4 Sebuah Penyelesaian dari Metode Numerik
- 1.1.5 4.3.6 Perangkat Lunak untuk Menyelesaikan ODEs
- 1.1.6 4.3.7 Metode Runge-Kutta Orde 4
- 1.1.7 4.3.9 ilustrasi redaman linier
- 1.1.8 4.3.10. Ilustrasi Redaman Linier Dengan Eksitasi Sinusoidal
- 1.1.9 4.3.12 Metode finite diference; Undamped, Linear Case
- 1.1.10 4.3.13 Metode finite diference; damping linier
- 1.1 Terjemahan
- 2 Artikel 1 Hasil diskusi : judul ..
- 3 Artikel 2 Hasil diskusi : judul ..=
- 4 Artikel .... Hasil diskusi : judul ...
Studi kasus dan Terjemahan
Ref. Linge S, Langtangen HP, Programming for Computations - A Gentle Introduction to Numerical Simulations with Python
Terjemahan
4.3.1 Penurunan Model yang Sederhana
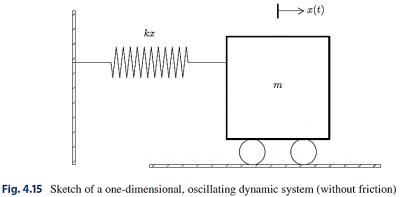
Banyak sistem keteknikan (engineering) berkaitan dengan osilasi, dan persamaan diferensial merupakan kunci utama untuk memahami, memprediksi, dan mengontrol osilasi. Kita mulai dengan model paling sederhana yang berkaitan dengan dinamika penting dari sistem osilasi. suatu benda dengan massa m melekat/dikaitkan pada pegas dan bergerak sepanjang garis tanpa gesekan, lihat Gambar 4.15 di samping untuk sketsa (rolling wheels menunjukkan “tidak ada gesekan”). Ketika pegas diregangkan (atau dikompresi), gaya pegas menarik (atau mendorong) bodi (penampang m) kembali dan bekerja "melawan" gerakan. Lebih tepatnya, misalkan x (t) adalah posisi bodi pada sumbu x, dimana bodi bergerak. Pegas tidak direntangkan ketika x= 0, sehingga gaya adalah nol, dan x= 0 karenanya posisi keseimbangan bodi. Gaya pegas adalah -kx, dimana k adalah konstanta yang diukur. Kami berasumsi bahwa tidak ada gaya lain (mis., Tidak ada gesekan). Hukum Newton ke-2 F=ma kemudian memiliki F=-kx dan a=x ̈ ,yang dapat ditulis ulang sebagai:
dengan memperkenalkan ω=√(k/m) (yang sangat umum).
Persamaan (4.42) adalah persamaan diferensial orde kedua, dan oleh karena itu kita memerlukan dua kondisi awal, satu pada posisi x(0) dan satu pada kecepatan x’(0). Di sini kita memilih bodi untuk berhenti, tetapi menjauh dari posisi setimbang:
Solusi tepat untuk Pers. (4.42) dengan kondisi awal ini adalah x(t)=X0 cosωT. Ini dapat dengan mudah diverifikasi dengan mensubsitusikan ke Pers. (4.42) dan memeriksa kondisi awal. Solusinya mengatakan bahwa sistem massa pegas berosilasi bolak-balik seperti yang dijelaskan oleh kurva kosinus.
Persamaan diferensial (4.42) muncul dalam banyak konteks lainnya. Contoh klasik adalah pendulum sederhana yang berosilasi bolak-balik. Buku-buku fisika berasal, dari hukum gerak kedua Newton, itu diperoleh:
dimana m adalah massa bodi di ujung pendulum dengan panjang L, g adalah percepatan gravitasi, dan ϴ merupakan sudut yang dibuat pendulum dengan vertikal. Mempertimbangkan sudut kecil ϴ, sin ϴ ≈ ϴ, dan kita dapatkan Pers. (4.42) dengan x = ϴ, ω=√(g/L) , x(0)=Θ, dan x’(0)=0, jika Θ merupakan sudut awal dan pendulum diam di t=0.
4.3.2 Solusi Numerik
Kita telah melihat metode numerik untuk mengendalikan turunan orde kedua, dan beberapa pilihan lainnya merupakan tambahan, akan tetapi kita mengetahu cara menyelesaikan persamaan turunan orde pertama dan bahkan sistem-sistem pada persamaan orde pertama. Dengan hanya sedikit, tetapi cukup umum, cara yang dapat kita tuliskan pada persamaan 4.42 sebagai sebuah sistem orde pertama dari 2 persamaan turunan. Kita memperkenalkan u=x dan v=x^'=u' sebagai 2 fungsi baru yang tidak diketahui. Dua persamaan yang sesuai muncul dari definisi v=u' dan persamaan asal (4.42):
(memperlihatkan bahwa kita dapat menggunakan u"=v') untuk menghilangkan turunan orde kedua dari hokum kedua newton). Selanjutnya kita dapat menerapkan metode forward euler untuk persamaan 4.43 dan 4.44, seperti yang sudah dilakukan pada section 4.2.2:
Sehingga menghasilkan skema komputasi sebagai berikut,
4.3.3 Memprogram Metode Numerik; Kasus Khusus
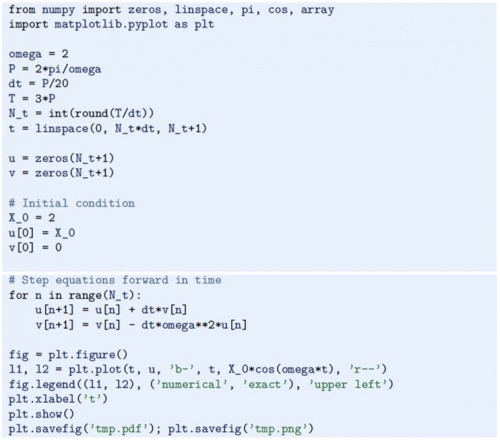
Program sederhana untuk (4.47) - ( 4.48) mengikuti ide yang sama seperti di bagian 4.2.3:
(Lihat file osc_FE.py.)
Karena kita sudah tahu solusi yang tepat sebagai u(t) = Xo cos ωt , kami beralasan sebagai berikut untuk menemukan interval simulasi yang sesuai [0,T] dan juga berapa poin kita harus memilih. Solusinya memiliki periode P = 2π/ω. (Periode P adalah waktunya perbedaan antara dua puncak u(t) ~ cos ωt curve). Simulasi untuk tiga periode fungsi cosinus, T = 3P, dan memilih Δt sehingga ada 20 Interval per periode menghasilkan Δt = P/20 dan total Nt = T/ Δt = t interval. Sisanya dari program ini adalah pengodean langsung dari skema Forward Euler.
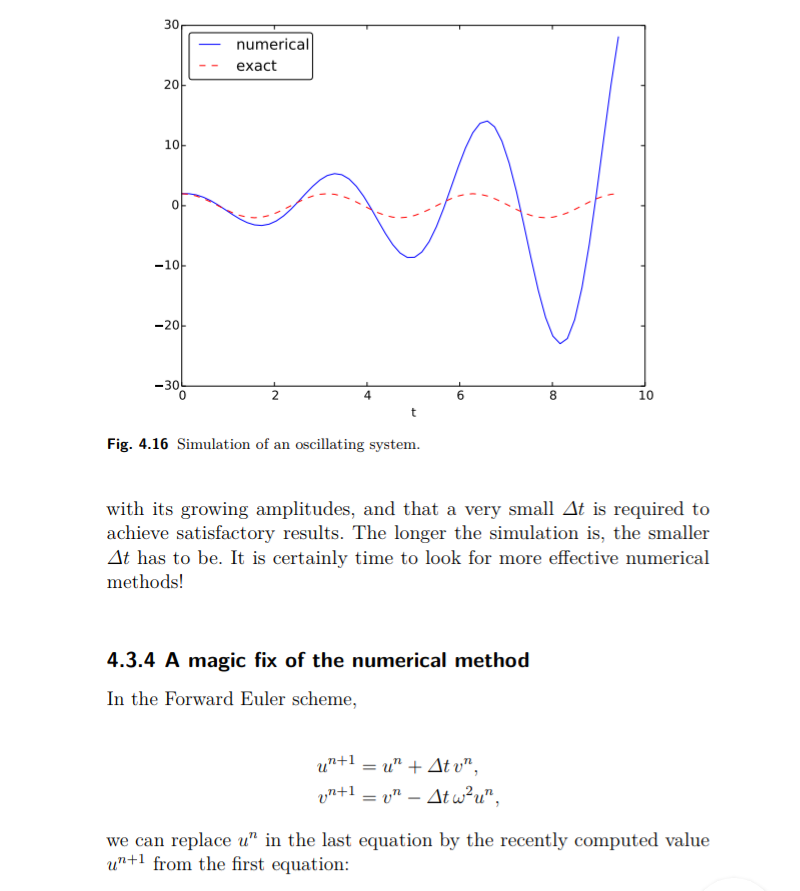
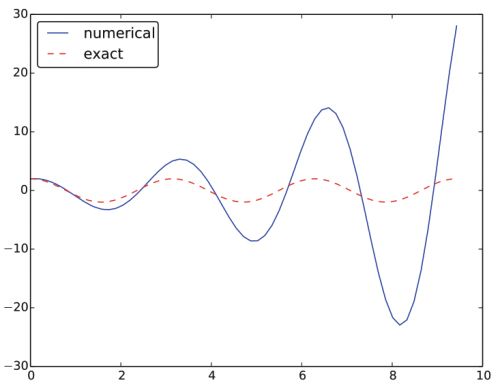
Gambar 4.16 menunjukkan perbandingan antara solusi numerik dan tepat solusi persamaan diferensial. Yang mengejutkan kami, solusi numeriknya terlihat salah. Apakah perbedaan ini disebabkan oleh kesalahan pemrograman atau masalah dengan metode Forward Euler?
Pertama-tama, bahkan sebelum mencoba menjalankan program, Anda harus menghitung dua langkah dalam putaran waktu dengan kalkulator sehingga Anda memiliki beberapa hasil antara untuk dibandingkan. Menggunakan X0 = 2. Dt = 0: 157079632679, dan ω = 2, kita mendapatkan u1 = 2, v = -1,25663706, u2 = 1,80260791, dan v2 = 2,51327412. Perhitungan semacam itu menunjukkan bahwa program itu tampaknya benar. (Kemudian, kita dapat menggunakan nilai-nilai tersebut untuk membangun tes unit dan fungsi tes yang sesuai.)
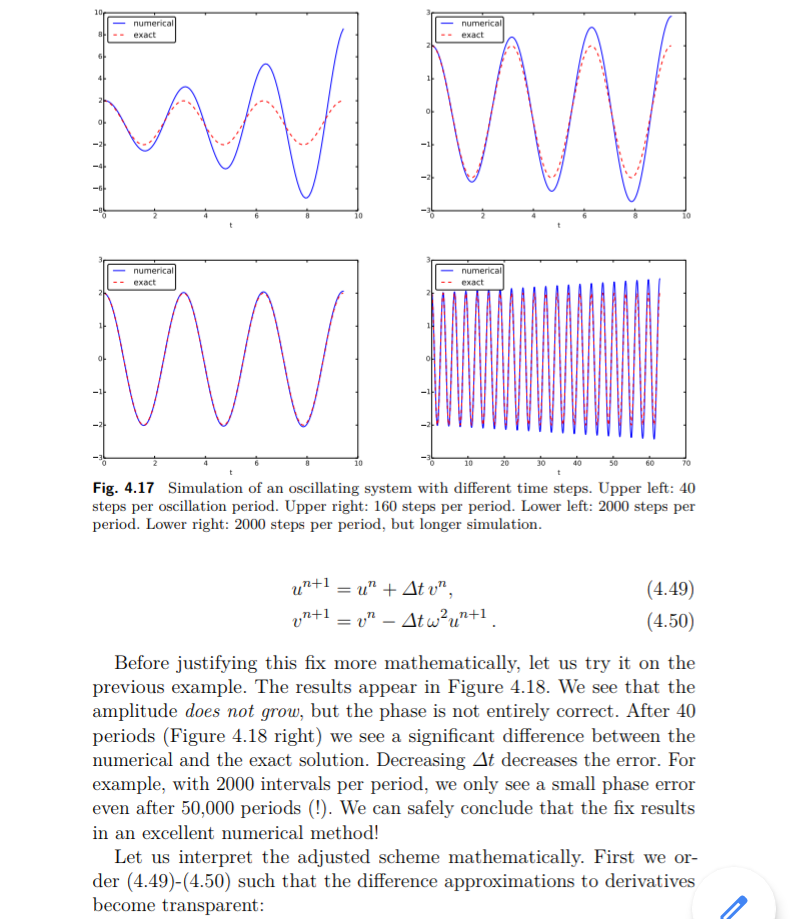
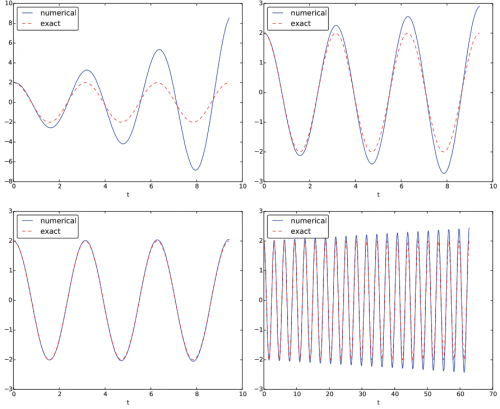
Langkah selanjutnya adalah mengurangi delta t parameter diskritisasi dan melihat apakah hasilnya menjadi lebih akurat. Gambar 4.17 menunjukkan solusi numerik dan tepat untuk kasus delta t = P / 40; P / 160; P / 2000. Hasilnya jelas menjadi lebih baik, dan resolusi terakhir memberikan grafik yang tidak dapat dibedakan secara visual. Namun demikian, resolusi terakhir melibatkan 6000 interval komputasi secara total, yang dianggap cukup banyak. Namun, ini bukan masalah pada laptop modern, karena perhitungan hanya membutuhkan sepersekian detik.
Meskipun 2000 interval per periode osilasi tampaknya cukup untuk solusi numerik yang akurat, grafik kanan bawah pada Gambar 4.17 menunjukkan bahwa jika kita meningkatkan waktu simulasi, di sini hingga 20 periode, ada sedikit pertumbuhan amplitudo, yang menjadi signifikan dari waktu ke waktu. . Kesimpulannya adalah bahwa metode Forward Euler memiliki masalah mendasar dengan amplitudo yang tumbuh, dan bahwa diperlukan delta yang sangat kecil untuk mencapai hasil yang memuaskan. Semakin lama simulasi, semakin kecil Delta t. Sudah pasti saatnya untuk mencari metode numerik yang lebih efektif!
4.3.4 Sebuah Penyelesaian dari Metode Numerik
Dalam skema Forward Euler,
kita dapat mengganti u^n pada persamaan terakhir dengan nilai u^n+1 yang baru dihitung dari persamaan pertama:
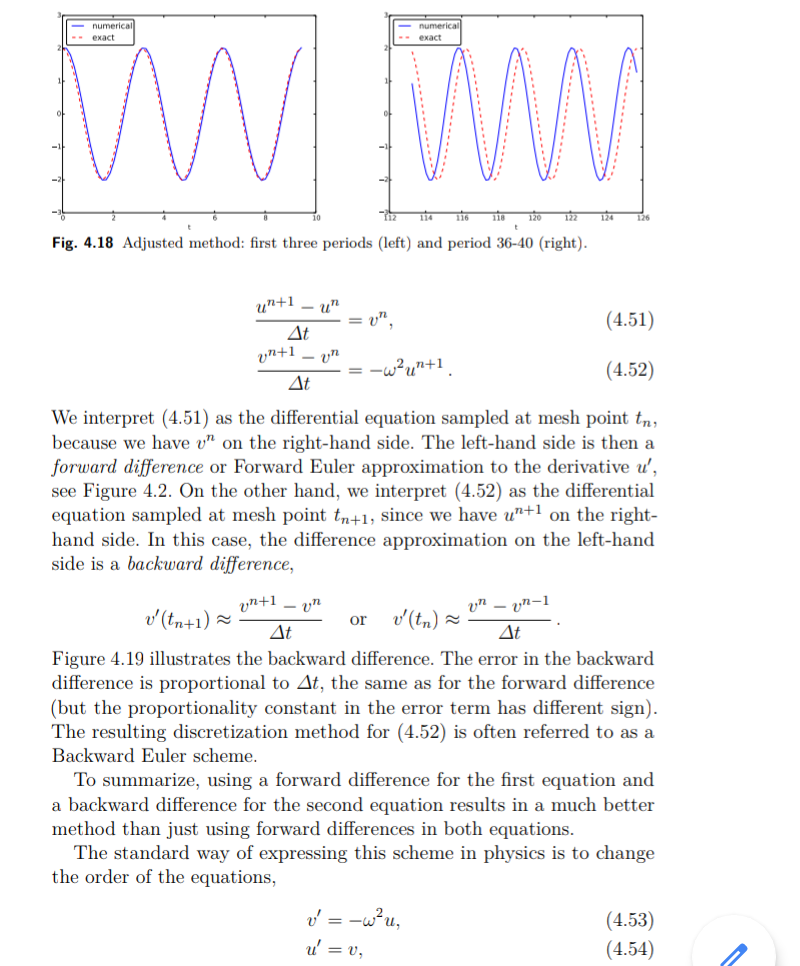
Sebelum membenarkan perbaikan ini secara matematis, mari kita coba pada contoh sebelumnya. Hasilnya muncul pada Gambar 4.18. Kita melihat bahwa amplitudo tidak tumbuh, tetapi fase tidak sepenuhnya benar. Setelah 40 periode (Gbr. 4.18 kanan) kita melihat signifikan perbedaan antara solusi numerik dan tepat. Penurunan t menurun kesalahan. Misalnya, dengan 2000 interval per periode, kami hanya melihat fase kecil kesalahan bahkan setelah 50.000 periode (!). Kita dapat menyimpulkan bahwa perbaikan tersebut menghasilkan metode numerik yang sangat baik! Mari kita tafsirkan skema yang disesuaikan secara matematis. Pertama kami memesan (4,49) - (4,50) sedemikian rupa sehingga perbedaan pendekatan terhadap derivatif menjadi transparan:
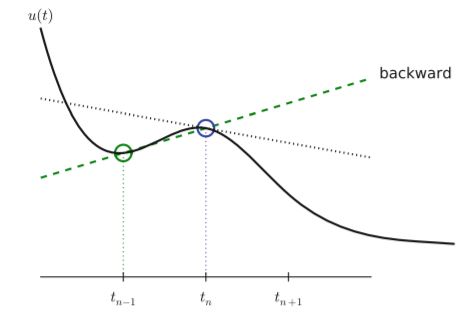
Kami menafsirkan (4,51) sebagai persamaan diferensial sampel pada titik mesh tn, karena kami memiliki vn di sisi kanan. Sisi kiri kemudian perbedaan maju atau Meneruskan perkiraan Euler ke turunan u0 , lihat Gambar 4.2. Di samping itu, kami menginterpretasikan (4,52) sebagai persamaan diferensial sampel pada titik mesh tnC1, karena kami miliki di sisi kanan.
Dalam hal ini, perbedaan aproksimasi pada sisi kiri adalah perbedaan ke belakang,
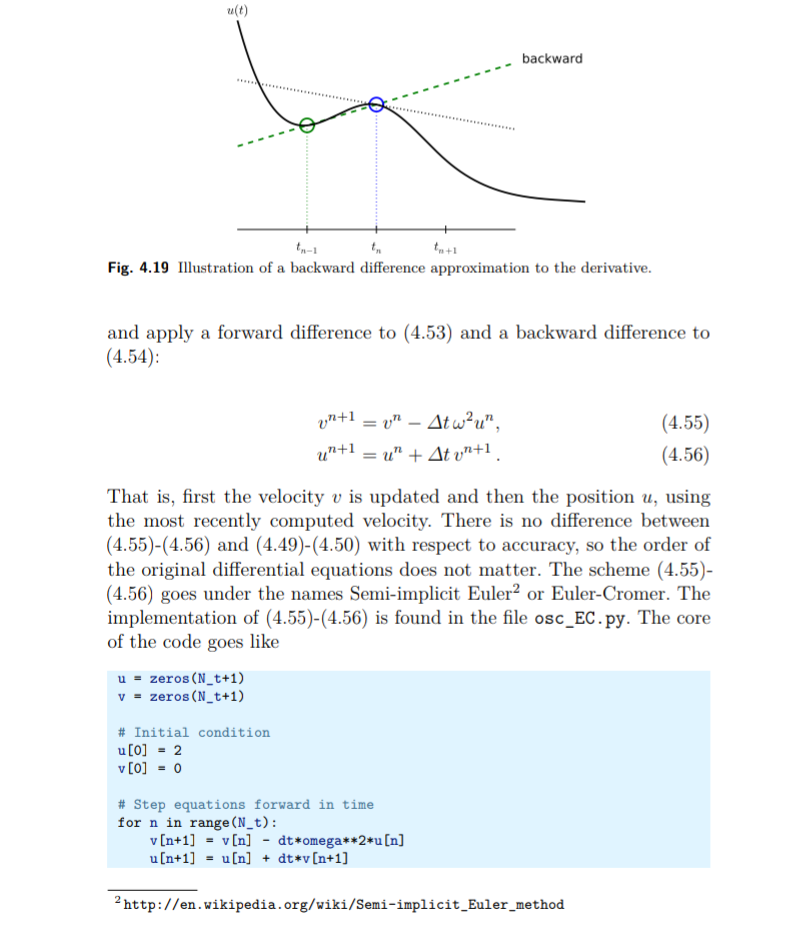
Gambar 4.19 mengilustrasikan perbedaan mundur. Kesalahan dalam perbedaan mundur sebanding dengan t, sama seperti untuk perbedaan maju (tetapi konstanta proporsionalitas dalam istilah kesalahan memiliki tanda yang berbeda). Diskretisasi yang dihasilkan metode untuk (4,52) sering disebut sebagai skema Backward Euler.
Untuk meringkas, gunakan perbedaan maju untuk persamaan pertama dan mundur Perbedaan untuk hasil persamaan kedua dalam metode yang jauh lebih baik daripada hanya menggunakan maju perbedaan dalam kedua persamaan.
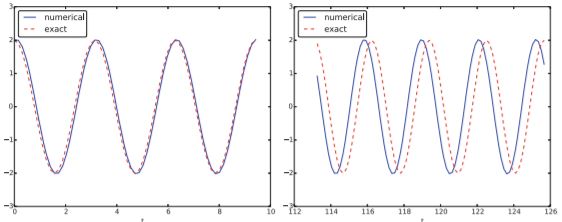
Cara standar untuk mengekspresikan skema ini dalam fisika adalah dengan mengubah urutan persamaan,
dan terapkan perbedaan maju ke (4,53) dan perbedaan mundur ke (4,54):
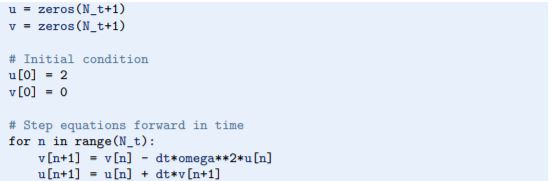
Artinya, pertama kecepatan v diperbarui dan kemudian posisi u, menggunakan kecepatan yang paling baru dihitung. Tidak ada perbedaan antara (4,55) - (4,56) dan (4,49) - (4,50) sehubungan dengan akurasi, jadi urutan persamaan diferensial asli tidak apa-apa. Skema (4.55) - (4.56) berada di bawah nama Semi-implisit Euler4 atau Euler-Cromer. Implementasi (4.55) - (4.56) ditemukan dalam file osc_EC.py. Inti dari kode itu seperti
4.3.6 Perangkat Lunak untuk Menyelesaikan ODEs
Terdapat banyak metode yang dapat digunakan untuk menyelesaikan ODEs, dan alangkah baiknya kita memilih akses yang mudah untuk mengimplementasikannya ke berbagai metode, terutama metode adaptif yang canggih dan kompleks yang dapat menyesuaikan nilai Δt secara otomatis untuk mendapatkan nilai akurasi yang ditentukan. Phyton Odespy3 merupakan salah satu perangkat yang dapat memberikan akses yang mudah ke berbagai metode numerik untuk menyelesaikan ODEs.
Salah satu contoh termudah dalam penggunaan Odespy adalah untuk menyelesaikan masalah u’ = u, u(0) = 2, untuk 100 time steps sampai t = 4:
import odespy
def f(u, t):
return u
method = odespy.Heun #or, e.g., odespy.ForwardEuler solver = method(f) solver.set_initial _condition(2) time_points = np.linspace(0, 4, 101) u. t = solver.solve (time_points)
Dengan kata lain, kalian mendefinisikan sebuah fungsi f(u, t), menginisialisasi sebuah objek penyelesaian Odespy, mengatur kondisi awal, menghitung titik waktu pengumpulan dimana anda menginginkan solusinya, dan bertanya mengenai solusinya. Variabel arrays u dan t dapat dibuat menjadi sebuah grafik secara langsung, yaitu: plot(t,u).
Fitur menarik yang dimiliki oleh Odespy ialah parameter permasalahan dapat menjadi sebuah argumen pada fungsi f(u, t) penggunanya. Sebagai contoh, apabila permasalahan ODE kita adalah u’ = -au + b, dengan 2 parameter yaitu a dan b, kita dapat menuliskan fungsi f kita menjadi
def f(u, t, a, b):
return -a*u + b
Sebagai tambahan, permasalahan yang bergantung pada argumen a dan b dapat ditransfer ke fungsi ini bila kita mengumpulkan nilainya dalam sebuah daftar atau tuple ketika membuat sebuah pemecahan Odespy dan menggunakan argumen f_args:
a = 2 b = 1 solver = method(f, f_args=[a, b])
Hal ini merupakan sebuah fitur yang baik karena parameter permasalahan haruslah selain sebagai sebuah variabel global – sekarang dapat menjadi sebuah argument dalam fungsi kita secara alami.
Menggunakan Odespy untuk menyelesaikan osilasi ODEs seperti u” + ω2u = 0, diformulasikan sebagai sebuah sistem u’ = v dan v’ = -ω2u, dilakukan sebagai berikut. Kita tentukan sebuah nilai time steps per periode dan hitung time steps yang diasosiasikan serta waktu akhir simulasi (T), cantumkan sebuah nilai periode untuk disimulasikan:
Import odespy
- Define the ODE system
- u’ = v
- v’ = -omega**2*u
def f(sol, t, omega=2):
u, v = sol
return [v, -omega**2*u]
- Set and compute problem dependent parameters
omega = 2 X_0 = 1 number_of_periods = 40 time_intervals_per_period = 20 from numpy import pi, linspace, cos P = 2*pi/omega #length of one period # length of one period dt = P/time_intervals_per_period # time step T = number_of_periods*P # final simulation time
- Create Odespy solver object
odespy_method = odespy.RK2 solver = odespy_method(f, f_args=[omega])
- The initial condition for the system is collected in a list
Solver.set_initial_condition([X_0, 0])
- Compute the desired time points where we want the solution
N_t = int(round(T/dt)) # no of time intervals Time_points = linspace(0, T, N_t+1)
- Solve the ODE problem
sol, t = solver.solve(time_points)
- Note: sol contains both displacement and velocity
- extract original variables
u = sol[:,0] v = sol[:,1]
Dua pernyataan terakhir menjadi penting karena dua fungsi u dan v di dalam sistem ODE tersebut tergabung bersama dalam sebuah array di dalam pemecahan Odespy. Solusi pada sistem ODE ditunjukan sebagai array 2 dimesi dimana kolom pertama (sol[:,0]) disimpan sebagai u dan kolom kedua (sol[:,1]) disimpan sebagai v. Mengeplot u dan v merupakan sebuah masalah dalam menjalankan plot(t, u, t, v).
Catatan
Di dalam fungsi tersebut kita menuliskan f(sol, t, omega) dibandingkan menulis f (u, t, omega) untuk mengindikasikan bahwa solusi pada f adalah solusi pada waktu t dimana nilai u dan t tergabung bersama: sol = [u,v]. Kita dapat juga menggunakan u sebagai argumen:
def f(u, t, omega=2):
u, v = u
return [v, -omega**2*u]
Ini hanya berarti kita mendefinisikan ulang nama u pada fungsi tersebut untuk merata-ratakan solusi pada waktu t untuk komponen pertama pada sistem ODE tersebut.
Untuk beralih ke metode numerik lain, tinggal substitusikan RK2 dengan nama yang sesuai dari metode yang diinginkan. Mengetik pydoc odespy pada terminal window memunculkan daftar dari metode yang dijalankan. Cara yang sangat sederhana dalam memilih metode ini menyarankan penambahan yang jelas dari kode diatas: kita dapat menentukan daftar metode, menjalankan semua metode, dan membandingkan setiap kurva u pada sebuah plot. Sebagaimana odespy juga mengandung skema Euler-Cromer, kita menulis kembali sistem ini dengan v’ = -w2u sebagai ODE pertama dan u’ = v sebagai ODE kedua, karena ini adalah pilihan standar ketika menggunakan metode Euler-Cromer (juga pada odespy):
def f(u, t, omega=2): v, u = u return [-omega**2*u, v]
Perubahan persamaan ini juga mempengaruhi kondisi awal: komponen pertama adalah nol dan yang kedua adalah X_0 maka kita perlu melewati daftar [0, X_0] untuk solver.set_ initial_condition.
Kode osc_odespy.py mengandung detail:
def compare(odespy_methods, omega, X_0, number_of_periods, time_intervals_per_period=20): from numpy import pi, linspace, cos P = 2*pi/omega # length of one period dt = P/time_intervals_per_period T = number_of_periods*P # If odespy_methods is not a list, but just the name of # a single Odespy solver, we wrap that name in a list # so we always have odespy_methods as a list if type(odespy_methods) != type([]): odespy_methods = [odespy_methods] # Make a list of solver objects solvers = [method(f, f_args=[omega]) for method in odespy_methods] for solver in solvers: solver.set_initial_condition([0, X_0]) # Compute the time points where we want the solution dt = float(dt) # avoid integer division N_t = int(round(T/dt)) time_points = linspace(0, N_t*dt, N_t+1) legends = [] for solver in solvers: sol, t = solver.solve(time_points) v = sol[:,0] u = sol[:,1] # Plot only the last p periods p = 6 m = p*time_intervals_per_period # no time steps to plot plot(t[-m:], u[-m:]) hold(’on’) legends.append(solver.name()) xlabel(’t’) # Plot exact solution too plot(t[-m:], X_0*cos(omega*t)[-m:], ’k--’) legends.append(’exact’) legend(legends, loc=’lower left’) axis([t[-m], t[-1], -2*X_0, 2*X_0]) title(’Simulation of %d periods with %d intervals per period’ % (number_of_periods, time_intervals_per_period)) savefig(’tmp.pdf’); savefig(’tmp.png’) show()
Fitur baru pada kode ini adalah kemampuan untuk mem-plot hanya periode p terakhir, yang memperbolehkan kita untuk menjalankan long time simulations dan melihat hasil akhir tanpa plot yang berantakan dengan terlalu banyak periode. Syntax t[-m:] mem-plot elemen m terakhir dalam t (indeks negatif dalam hitungan susunan/daftar Pyhton dari akhir).
Kita bisa membandingkan metode Heun (atau setara metode RK2) dengan skema Euler-Crome:
compare(odespy_methods=[odespy.Heun, odespy.EulerCromer], omega=2, X_0=2, number_of_periods=20, time_intervals_per_period=20)
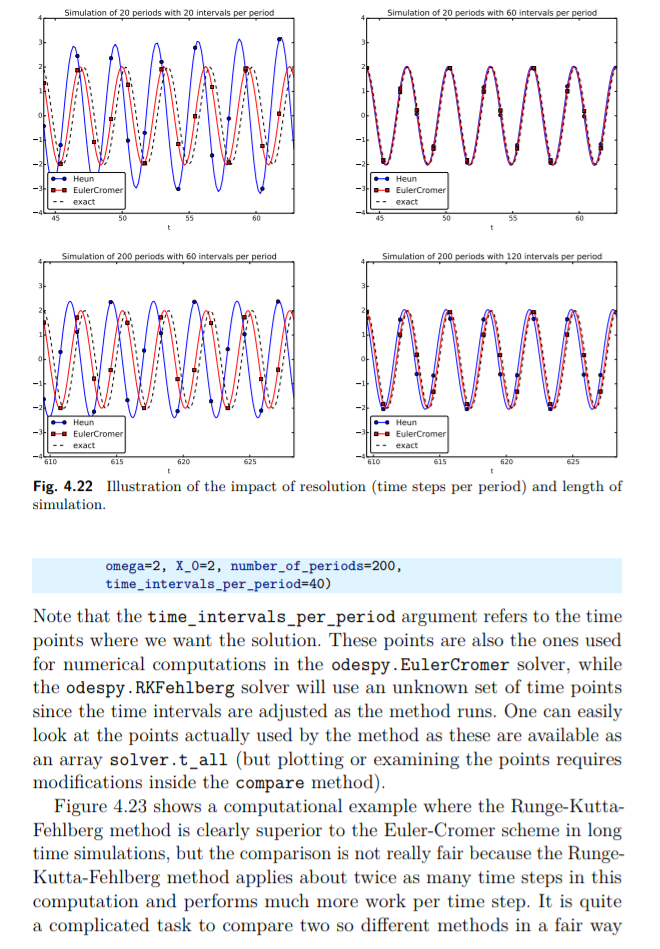
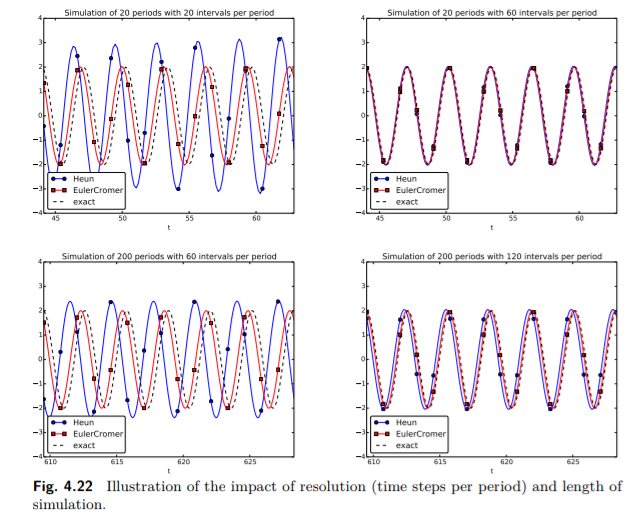
Gambar 4.22 menunjukkan bagaimana metode Heun (garis biru dengan piringan kecil) memiliki error yang cukup besar pada amplitude dan fase sesudah setelah periode 14-20 (kiri atas), namun menggunakan sebanyak tiga kali langkah waktu membuat kurvanya hampir sama (kanan atas). Akan tetapi setelah periode 194-200 error tersebut telah berkembang (kiri bawah), tetapi dapat cukup dikurangi dengan mengurangi separuh langkah waktu (kanan bawah).
Dengan semua metode di Odespy, sekarang menjadi mudah untuk mulai menjelajahi metode-metode lain, seperti perbedaan mundur (backward differences) bukannya perbedaan maju (forward differences) yang digunakan dalam skema Forward Euler. Latihan 4.17 mengatasi permasalahan tersebut.
Odespy berisi metode adaptif yang cukup canggih di mana pengguna "dijamin" untuk mendapatkan solusi dengan akurasi yang ditentukan. Tidak ada jaminan matematis, tetapi error untuk sebagian besar kasus tidak akan menyimpang secara signifikan dari toleransi pengguna yang mencerminkan keakuratan. Metode yang sangat populer dari jenis ini adalah metode Runge-Kutta-Fehlberg, yang menjalankan metode Runge-Kutta orde 4 dan menggunakan metode Runge-Kutta orde 5 untuk memperkirakan error sehingga dapat disesuaikan untuk menjaga error di bawah toleransi. Metode ini juga dikenal luas sebagai ode45, karena itulah nama fungsi yang mengimplementasikan metode ini di Matlab. Kita dapat dengan mudah menguji metode Runge-Kutta-Fehlberg segera setelah kita tahu nama Odespy yang sesuai, yaitu RKFehlberg:
compare(odespy_methods=[odespy.EulerCromer, odespy.RKFehlberg], omega=2, X_0=2, number_of_periods=200, time_intervals_per_period=40)
Perhatikan bahwa argumen time_intervals_per_period mengacu pada titik waktu di mana kami ingin solusinya. Poin-poin ini juga yang digunakan untuk perhitungan numerik dalam pemecah odespy.EulerCromer, sedangkan pemecah odespy.RKFehlberg akan menggunakan satu set titik waktu yang tidak diketahui karena interval waktu disesuaikan ketika metode berjalan. Orang dapat dengan mudah melihat titik-titik yang sebenarnya digunakan oleh metode karena ini tersedia sebagai himpunan solver.t_all (tetapi merencanakan atau memeriksa titik-titik membutuhkan modifikasi di dalam metode perbandingan).
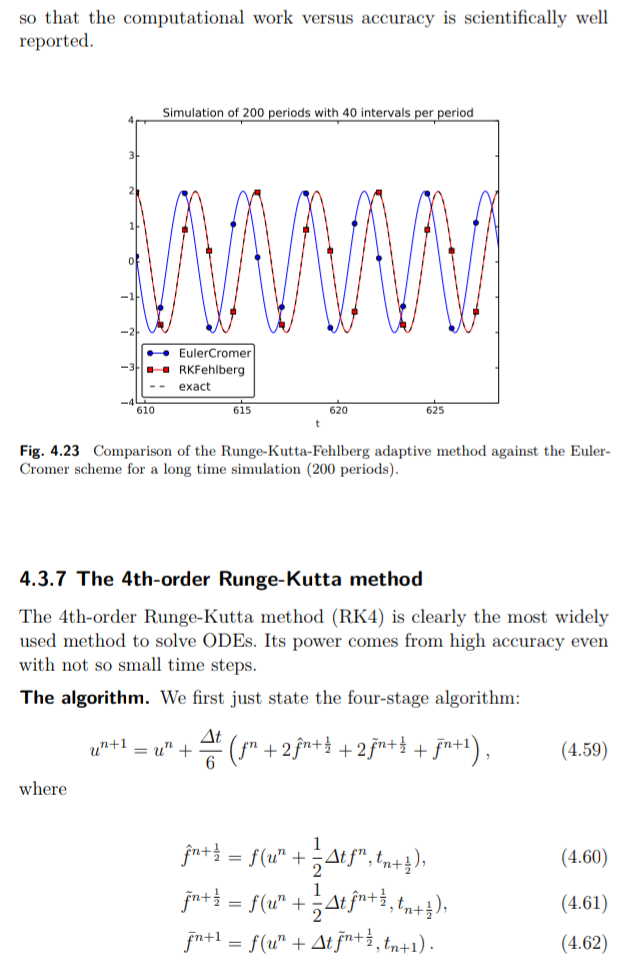
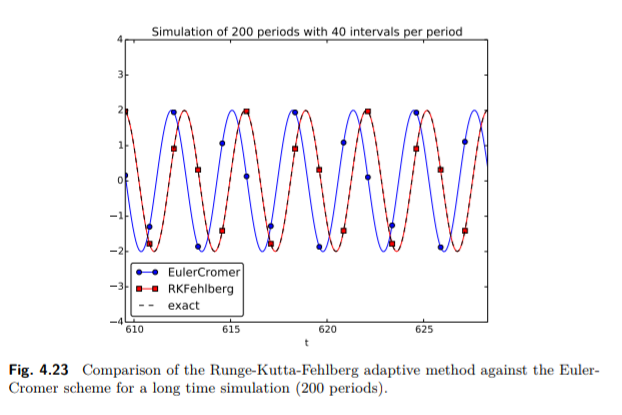
Gambar 4.23 menunjukkan contoh komputasi di mana metode Runge-Kutta-Fehlberg jelas lebih unggul daripada skema Euler-Cromer dalam simulasi yang lama, tetapi perbandingannya tidak terlalu adil karena metode Runge-Kutta_Fehlberg berlaku sekitar dua kali lebih banyak langkah waktu dalam hal perhitungan ini dan melakukan lebih banyak pekerjaan per langkah waktu. Ini adalah tugas yang cukup rumit untuk membandingkan dua metode yang sangat berbeda dalam cara yang wajar sehingga pekerjaan komputasi versus akurasi dilaporkan secara ilmiah dengan baik.
4.3.7 Metode Runge-Kutta Orde 4
Metode Runge-Kutta Orde 4 adalah metode yang sering digunakan secara luas untuk menyelesaikan ODEs, karena menghasilkan data dengan tingkat akurasi yang tinggi bahkan dalam time step yang tidak terlalu kecil.
Algoritma; Pertama-tama kita nyatakan algoritma 4-stage
Dimana
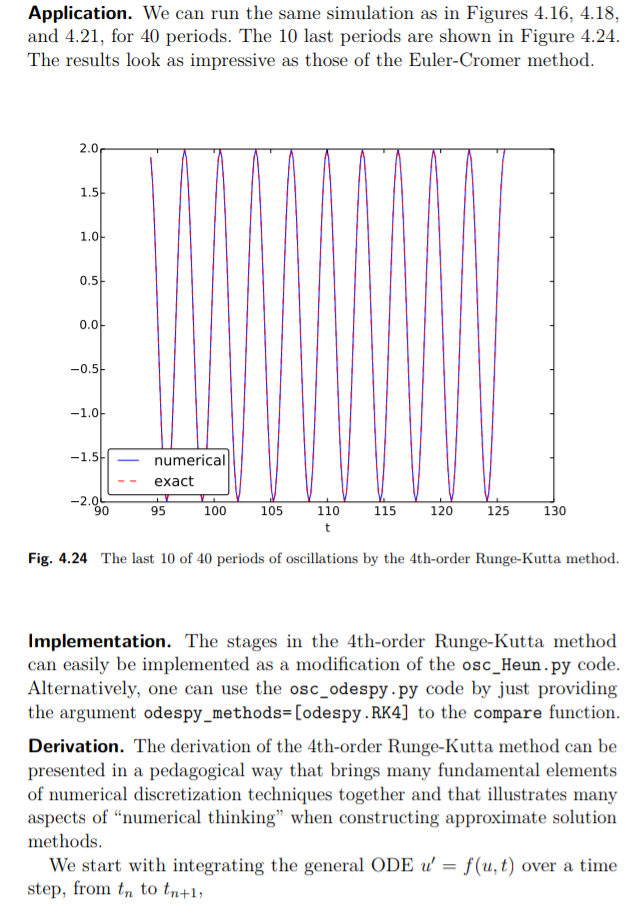
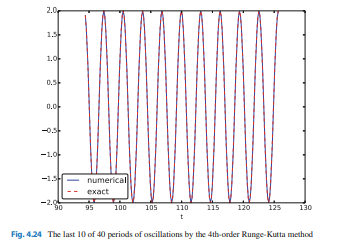
Aplikasi; Kita bisa menjalankan simulasi seperti pada Figs. 4.16, 4.18, dan 4.21, untuk 40 periode. 10 periode terakhir ditunjukan melalui Fig. 2.24. Hasil yang ditunjukan terlihat impresif sebagaimana penggunaan metode Euler-Cromer.
Implementasi; Tingkatan dalam metode Runge-Kutta orde-4 bisa dengan mudah diimplementasikan sebagai modifikasi dari osc_Heun.py code. Sebagai alternatif, salah satu dapat menggunakan osc_odespy.py code dengan menyediakan argumen odespy_methods-[odespy.RK4] untuk membandingkan fungsi.
Derivasi; Derivasi dari metode Runge-Kutta orde-4 dapat disajikan dengan cara pedagogis yang menyatukan banyak elemen fundamental dari teknik diskritisasi numerik dan bisa menggambarkan banyak aspek “numerical thinking ”ketika membangun perkiraan metode solusi.
Kita mulai dengan mengintegrasikan general ODE dari waktu ke waktu, mulai dari tn sampai t(n_1),
Tujuan dari komputasi , ketika
pada saat ini lebih dikenal dengan nilai u. Tantangan mengintegralkan muncul ketika integrand mengandung u yang tidak diketahuai antara tn sampai t(n+1).
Integral tersebut dapat diperkirakan dengan menggunakan Simpson’s rule yang telah terkenal
Permasalahan dengan persamaan ini adalah kita tidak mengetahui nilai dari dan
karena hanya u^n yang tersedia dan hanya f^n yang dapat dihitung.
Untuk melanjutkan, idenya dalah menggunakan berbagai perkiraan untuk dan
berdasarkan penggunaan skema yang telah diketahui untuk ODE dalam interval
dan
. Mari kita bagi persamaan integral menjadi empat suku.
Dimana ,
, dan
adalah pendekatan untuk
dan
yang dapat digunakan pada perhitungan. Untuk
dapat menggunakan pendekatan untuk
berdasarkan tahap Forward Euler pada size
Persamaan ini mempermudah prediksi , sehingga untuk
kita dapat mencoba metode Backward Euler untuk memperkirakan
Dengan sebagai pendekatan untuk
, pada akhirnya bentuk akhir dari
dapat menggunakan metode midpoint (atau central difference, juga disebut metode Crank-Nicholson) untuk memperkirakan
.
Kita telah menggunakan metode Forward dan Backward Euler, juga centered difference approximation pada konteks Simpsons rule. Diharapkan kombinasi dari metode ini dapat menghasilkan overall time stepping dari ke
yang lebih akurat dibandingkan individual steps (yang memiliki error proportional dengan
dan
). Hal ini benar bahwa: error numerik yang terjadi seperti
Untuk konstanta C, artinya error lebih cepat mendekati nol ketika time step size dikurangi, dibandingkan dengan metode Forward Euler
, metode Euler-Cromer
,atau Runge Kutta orde 2, atau metode Heuns
.
Perhatikan bahwa Metode Runge-Kutta Orde 4 sepenuhnya eksplisit jadi tidak diperlukan untuk menyelesaikannya dengan persamaan aljabar baik secara linier maupun non linier, terlepas dari apa yang terlihat pada f. Namun nilai kesetabilannya kondisional dan bergantung pada nilai f tersebut. Ada sebuah bagian besar dari metode implisit Runge-Kutta yang nilai kesetabilannya tidak kondisional. namun diperlukan solusi dari persamaan aljabar yang melibatkan nilai f pada setiap "time step". Odespy dapat dimanfaatkan untuk mendukung penyelesaian dari banyak metode Runge-Katta yang eksplisit. Tetapi belum bisa digunakan untuk metode Runge-Katta yang implisit.
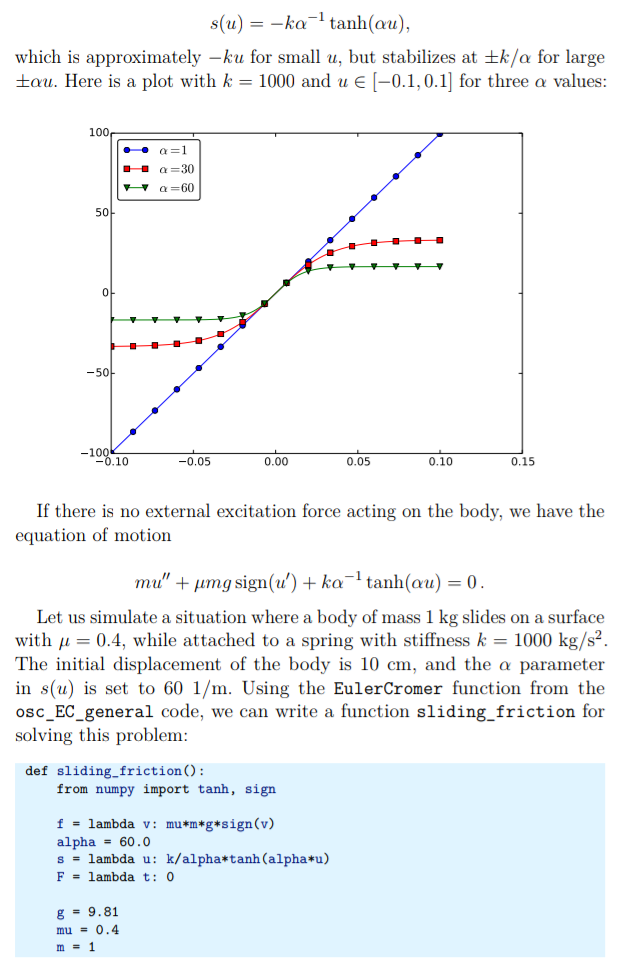
4.3.9 ilustrasi redaman linier
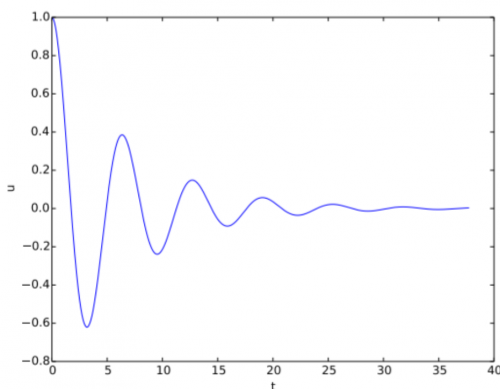
Kami menganggap sistem rekayasa dengan pegas linier, s(u) = kx, dan peredam kental, di mana gaya peredaman adalah porpotional terhadap u', f(u') = bu', untuk beberapa konstanta b > 0. Pilihan ini dapat memodelkan sistem pegas vertikal di dalam mobil (tetapi insinyur sering suka menggambarkan sistem tersebut dengan massa bergerak horizontal seperti yang digambarkan pada Gambar 4.25). kita dapat memilih nilai-nilai sederhana untuk konstanta untuk mengilustrasikan efek dasar redaman (dan kegembiraan selanjutnya). Memilih osilasi sebagai fungsi u(t) = cos t sederhana dalam kasus tak teredam, kita dapat menetapkan m = 1, k = 1, b = 0,3, Uo = 1, Vo = 0. Fungsi berikut mengimplementasikan kasus ini:
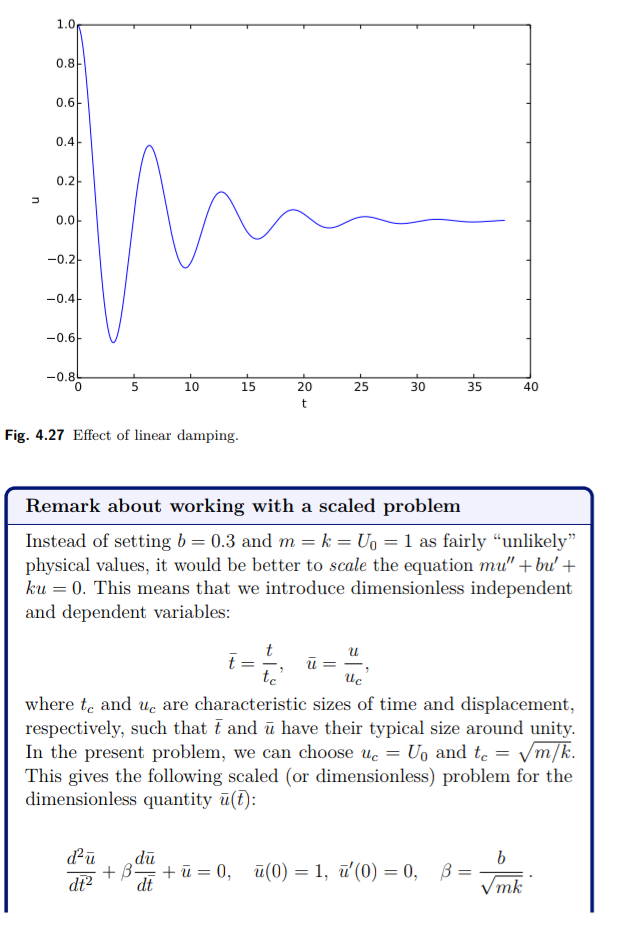
Fungsi plot_u adalah kumpulan plot untuk merencanakan u(t), atau bagian darinya. Gambar 4.27 menunjukkan efek dari bu': kita memiliki osilasi dengan (perkiraan) periode 2π, seperti yang diharapkan, tetapi amplitudo teredam secara efisien.
Komentar mengenai pekerjaan dengan masalah berskala
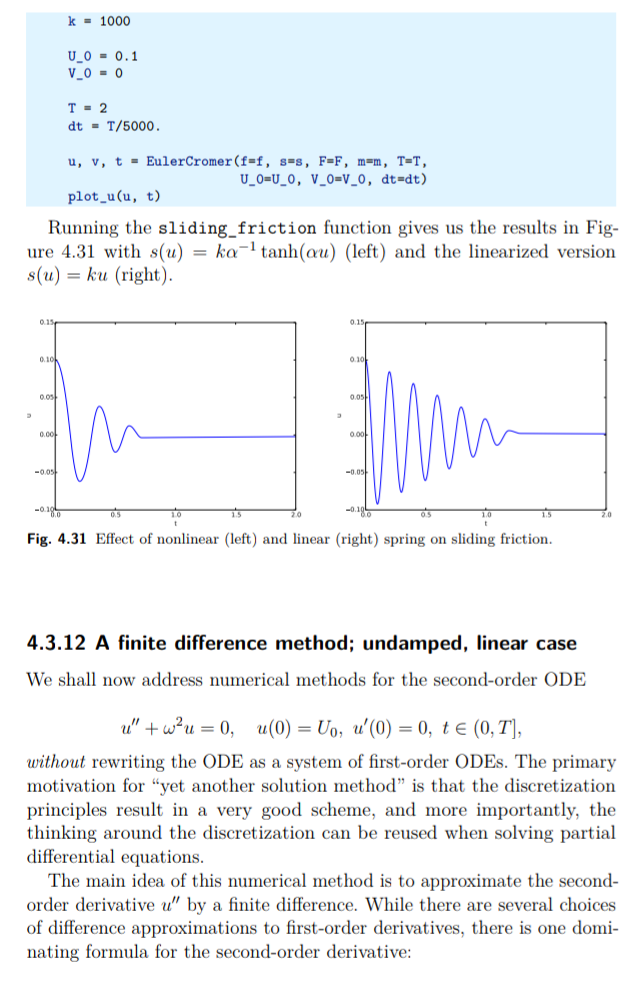
Alih-alih menetapkan b = 0,3 dan m = k = Uo = 1 sebagai nilai fisik yang “tidak mungkin”, akan lebih baik untuk skala persamaan mu" + bu' + ku = 0. Ini mengartikan bahwa kita memasukan variabel independen dan dependen yang tak berdimensi :
Di mana tc dan uc adalah ukuran karakteristik waktu dan perpindahan, sehingga ![]() dan
dan ![]() memiliki ukuran tipikal mereka didekat kesatuan. Dalam masalah ini, kita dapat memilih
memiliki ukuran tipikal mereka didekat kesatuan. Dalam masalah ini, kita dapat memilih ![]() dan
dan ![]() . Ini memberikan masalah yang berskala (atau tanpa dimensi) berikut untuk kuantitas tak berdimensi
. Ini memberikan masalah yang berskala (atau tanpa dimensi) berikut untuk kuantitas tak berdimensi ![]() :
:
Faktnya adalah hanya ada satu parameter fisik di kasus ini: angka β. Menyelesaikan masalah ini begitu juga terkait dengan masalah utama dengan parameter yaitu m = k = Uo = 1 dan b = β. Tetapi untuk menyelsaikan masalah dengan satuan lebih umum: jika kita memdapatkan solusi ¯u(¯t;β), kita dapat menemukan solusi fisik pada kasus ini, dikarenakan :
Selama β didapat, kita dapat menemukan u untuk Uo , k, dan m dengan rumus diatas, dengan begitu pengerjaan simulasi dapat dipersingkat waktu. Ini menunjukkan pengerjaan dengan skala atau masalah satuan.
4.3.10. Ilustrasi Redaman Linier Dengan Eksitasi Sinusoidal
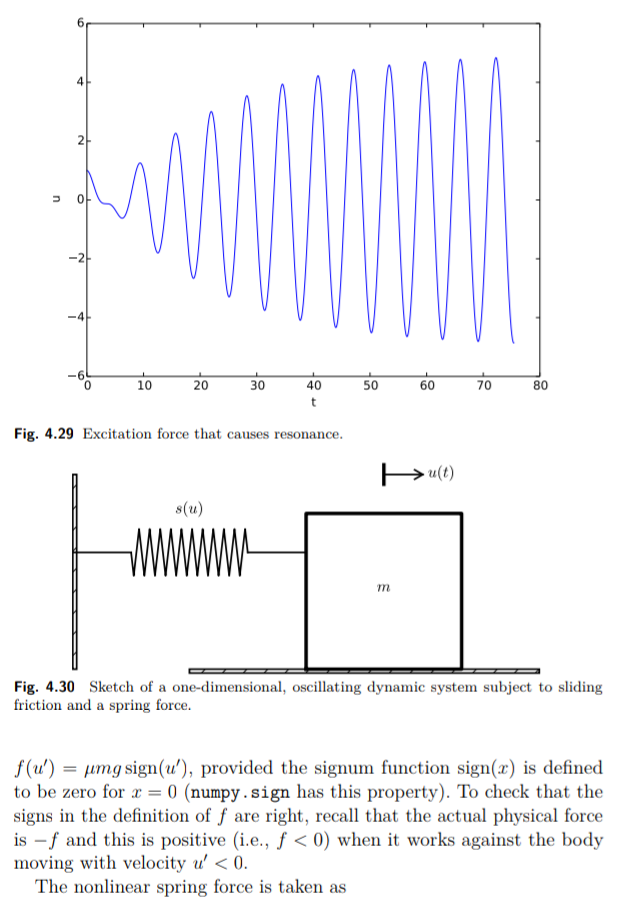
Sekarang kita akan memperluas contoh sebelumnya untuk menambah beberapa gaya osilasi eksternal pada sistem: F (t) = Asin (wt). Mengendarai mobil di jalan dengan lonjakan sinusoidal mungkin memberikan eksitasi eksternal pada sistem pegas di mobil (w terkait dengan kecepatan mobil).
from math import pi,sin
w = 3
A = 0.5
F = lambda t: A*sin(w*t)
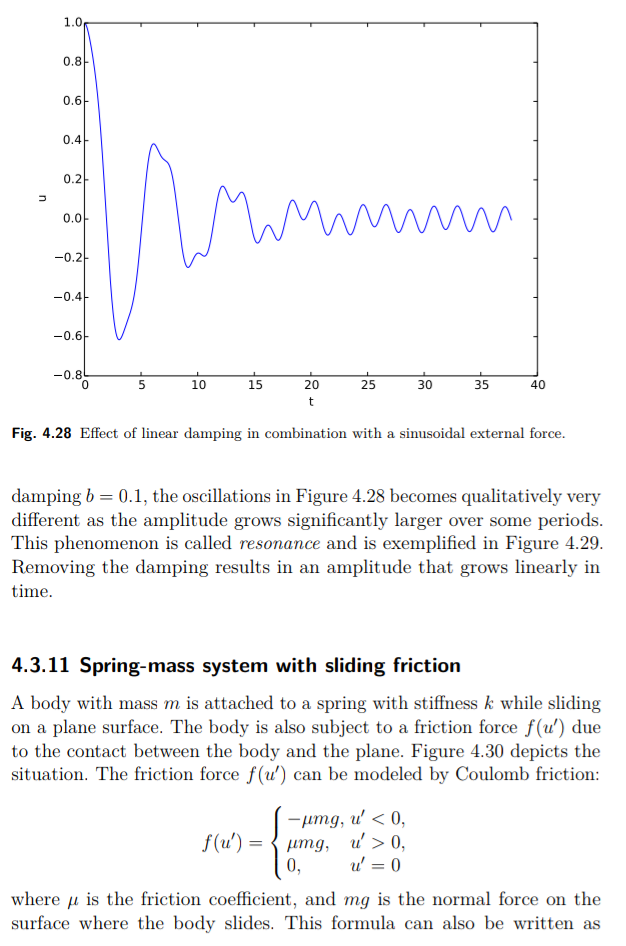
kita dapatkan grafik pada gambar 4.28 .Perbedaan yang mencolok dari Gambar 4.27 adalah bahwa osilasi dimulai sebagai sinyal cos t teredam tanpa banyak pengaruh gaya eksternal, tetapi kemudian osilasi bebas dari sistem yang tidak teredam (cos t) u’’ + u = 0 mati dan gaya eksternal 0: 5 sin.(3t) menimbulkan osilasi dengan periode yang lebih pendek 2phi/3. Dianjurkan untuk menggunakan beberapa nilai A yang lebih besar dan beralih dari sinus ke acosinus dalam F dan mengamati efeknya. Jika mencarinya di dalam buku fisika, Anda dapat menemukan solusi analitik yang tepat untuk masalah persamaan diferensial dalam kasus ini.
4.3.12 Metode finite diference; Undamped, Linear Case
Selanjutnya kita akan membahas metode numerik untuk ODE orde kedua
u^+ω^2 u=0, u(0)=U_0,u^' (0)=0,t∈(0,T]
tanpa menulis ulang ODE sebagai sistem ODE orde pertama. Motivasi utama untuk "metode solusi lain" adalah bahwa prinsip-prinsip diskritisasi menghasilkan skema yang sangat baik, dan yang lebih penting, pemikiran seputar diskritisasi bisa digunakan kembali ketika memecahkan persamaan diferensial parsial. Gagasan utama dari metode numerik ini adalah untuk memperkirakan urutan kedua turunan u dengan selisih terbatas. Sementara ada beberapa pilihan perbedaan perkiraan untuk derivatif orde pertama, ada satu rumus yang mendominasi untuk turunan orde kedua:
Error dalam perkiraan tersebut proporsional terhadap ∆t^2. Biarkan ODE valid di beberapa titik waktu yang berubah ubah t_n,
u^ (t_n )+ ω^2 u (t_n )=0
Selanjutnya memasukkan rumus perkiraan (4.74) diatas, sehingga di dapatkan
Sekarang diasumsikan bahwa u^(n-1) dan u^n sudah dihitung, dan u^(n+1) adalah yang baru tidak diketahui. Memecahkan sehubungan dengan u^(n+1)
Masalah besar muncul ketika kita ingin memulai skema. Kita tahu bahwa u^0 = U_0, tetapi menerapkan (4,76) untuk n=0 untuk menghitung u^1
4.3.13 Metode finite diference; damping linier
Sebuah isu kunci adalah bagaimana untuk mengkonferensi skema dari daerah 4.3.12 ke persamaan diferensial dengan lebih banyak istilah. Kita mulai dengan kasus linear penempatan f (u') = bu', kemungkinan gaya per nonlinear s(u), dan sebuah gaya excitation F(t):
Kita harus cari perkiraan perbedaan yang tepat untuk u' di dalam bu'. Sebuah pilihan yang baik adalah perbedaan berpusat
Sampling persamaan pada titik tn,
dan memasukkan perkiraan perbedaan terhingga pada u" dan u' hasil dalam
dimana F" adalah notasi pendek untuk F(t). Persamaan (4.81) adalah linear dalam
u^(n+1) tak diketahui kita dapat dengan mudah memecahkan untuk kuantitas ini: