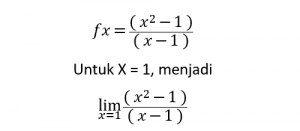Difference between revisions of "Miftah Dhia Falah"
Miftah.dhia (talk | contribs) (→Tugas 4) |
Miftah.dhia (talk | contribs) (→Tugas 4) |
||
| Line 196: | Line 196: | ||
''5 Maret 2020'' | ''5 Maret 2020'' | ||
| − | Pada asistensi tanggal 3 Maret 2020, kami telah diajarakan menggunakan CFD dan perhitungan regresi linier untuk mengetahui nilai persamaan kudarat maupun persamaan biasa dari suatu persoalan berdasarkan beberapa data yang didapat. | + | Pada asistensi tanggal 3 Maret 2020, kami telah diajarakan menggunakan CFD dan perhitungan regresi linier |
| + | untuk mengetahui nilai persamaan kudarat maupun persamaan biasa dari suatu persoalan berdasarkan beberapa data yang didapat. | ||
| − | Kemudian menggunakan CFD kita menghitung hambatan uss berdasarakan pengaturan yang telah dilakukan sebelumnya, kemudian execute semua data tersebut. Dan menghasilkan, beberapa data yang ada dibawah ini. | + | Kemudian menggunakan CFD kita menghitung hambatan uss berdasarakan pengaturan yang telah dilakukan sebelumnya, |
| + | kemudian execute semua data tersebut. Dan menghasilkan, beberapa data yang ada dibawah ini. | ||
[[File:Cfd4miftah.jpg|500px|left]][[File:Cfd7miftah.jpg|500px|right]] | [[File:Cfd4miftah.jpg|500px|left]][[File:Cfd7miftah.jpg|500px|right]] | ||
| − | Dari gambar kedua diatas didapatkan nilai hambatan drag kapal sebesar 304,46 | + | Dari gambar kedua diatas didapatkan nilai hambatan drag kapal sebesar 304,46 untuk contoh dari 5 m/s sedangkan rata - rata kecepatan kapal |
| + | yang akan ada berkisar antara 11 m/s - 20 m/s. Kemudian metode tersebut diulang dari awal dengan mengubah kecepatan kapal tersebut | ||
| + | dari 11 m/s - 20 m/s. Dan pada akhirnya didapatkan data kapal sebagai berikut. | ||
| + | |||
| + | [[File:Data kecepatan cfd.jpg|500px|left]] | ||
| + | |||
| + | Setelah didapatkan kemudian sepuluh data tersebut dimasukkan kedalam perhitungan menggunakan python dan didapatkan, | ||
| + | |||
| + | [[File:Cfdpiton1.jpg|20px|left]] | ||
| + | |||
| + | Dari gambar diatas didapatkan output berupa persamaan yang dicari dalam bentuk 3 angka yang akan dimasukkan kedalam persamaan kuadrat. | ||
| + | Dan bentuk grafik dari data tersebut. Sehingga persamaan drag terhadap kecepatan yang dicari sebagai berikut, | ||
| + | |||
| + | <b>Y= 5.05963636X² - 0.49635152x + 2.23081212</b> | ||
== Progress Belajar - Week 3 == | == Progress Belajar - Week 3 == | ||
Revision as of 22:01, 5 March 2020
بِسْمِ اللهِ الرَّحْمنِ الرَّحِيمِ
Contents
Personal Information
Name : Miftah Dhia Falah
NPM : 1806149684
Jurusan : Teknik Perkapalan
Date of Birth : 14 december 2000
Biography at Glance
Inspired by Atta S Gibran
Pengalaman mengenai perkomputeran dan pemrograman
- MS Word
- MS Excell
- MS Power Point
- Autocad
- Inventor
- Maxsurf
- Thinkercad
- Basic HTML
- Basic C
Daftar tiap pertemuan
Pertemuan 2
14 February 2020
Dari buku ( aan Kiusalaas, Numerical Methods in Engineering with Python 3, cambridge university press )
saya menemukan soal yang menarik pada bab 3 section 3.2 ,
soal ini sangat menarik bagi saya karena salah satu bentuk dari implementasi matematika dalam pengambilan rata2 dalam data percobaan.
metode ini juga sangat dibutuhkan dalam pengolahan data percobaan khususnya bagi mahasiswa yang akan menjalani
skripsi, disertasi, maupun thesis. materi ini sendiri masuk kepada bidang ilmu statistika dan problabilitas dari suatu himpunan data.
Pertemuan 3
21 February 2020
Pemodelan suatu kejadian, namun perlu diketahui bahwa pemodelan suatu fenomena tidak akan menyamai fenomena aktual yang terjadi
karena persamaan yang dimodelkan ini hanyalah suatu bentuk pendekatan dari sebenarnya. yang dimana setelah ditemukan model matematika dari persamaamn tesebut
kemudian dilakukan kalkulasi oleh perhitungan secara numerik digital. Contoh penerapan dari pemodelan ini adalah gerak osilasi pada pegas
yang dimana dapat diformulasikan menjadi rumus pemodelan matematika yaitu F = k dX.
Seperti yang dijelaskan sebelumnya bahwa semua rumus dapat dimodelkan serta memiliki asal mula yang sama atau merujuk pada konservasi energi,
prinsip ini sendiri biasanya sangat memainkan peran penting dalam suatu bentuk kerja dari daya yang dihasilkan maupun kalor yang bekerja.
Tugas 1
Soal Tugas 1
Jawaban Manual
Diberikan fungsi seperti pada gambar di soal sebelumnya, dan dicari niali dari fungsi tersebut jika mendekati nilai 1.
Saat fungsi tersebut dimasukkan nilai x = 1 secara langsung maka menghasilkan 0/0,
hal ini mengharuskan kita untuk memecah persamaan tersebut menjadi lebih sederhana dan melakukan metoda eliminasi.
dari hasil perhitungan diatas, diketahui bahwa nilai fungsi tersebut tidak 0/0 setelah dilakukan eliminasi,
dan fungsi akhir setelah dilakukannya eliminasi menjadi f(x) = ( x + 1 ), dengan memasukkan nilai x sebesar 1
f(1) = ( 1 + 1 ) = 2
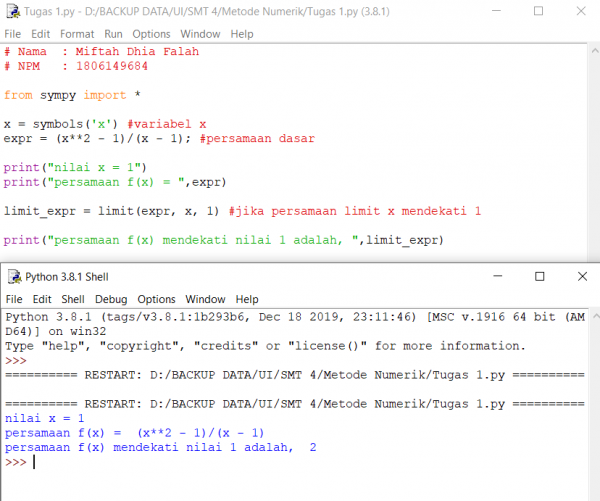
Jawaban Menggunakan Python
Komputasi telah saya lakukan menggunakan Python ver 3.8.1
Tugas 2
Soal Tugas 2.1
Soal ini diambil dari buku ( aan Kiusalaas, Numerical Methods in Engineering with Python 3, cambridge university press )
pada bab 3 section 3.2 , no 2.
Jawaban Manual
pada perhitungan manual data dikelompokkan dan diolah berdasarkan perhitungan dibawah ini,
Rumu perhitungan dan pengolahan data manual didapat dari buku Prinsip-prinsip Statistik untuk Teknik dan Sains
oleh : Prof. Dr. Ir. Harinaldi, M.Eng.
sehingga didapatkan persamaan regresi linear-nya yaitu, y = -0.02 + x
Jawaban Menggunakan Python
Komputasi telah saya lakukan menggunakan Python ver 3.8.1
dengan meng-import function numphy
serta function matplotlib untuk menampilkan plotting garis
dari perhitungan menggunakan python diatas, diketahui bahwa persamaan garis regresi linear tersebut adalah
y = -0.02 + x yang dimana hasil ini selaras dengan perhitungan manual data tersebut. Dengan bentuk garis seperti diatas
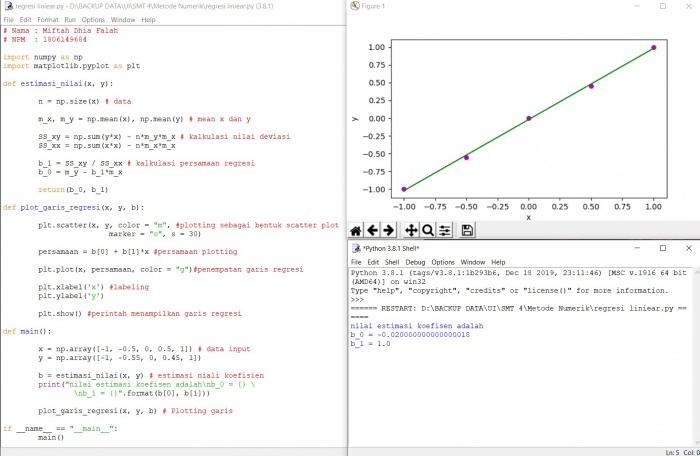
Soal Tugas 2.2
Suatu bola dengan berat 25 kg jatuh dari ketinggian 300 meter dalam keadaan diam. Bola ini memiliki hambatan jatuh bernilai 100 N.
Pada detik ke 5, berapakah jarak yang telah ditempug bola tersebut?
Jawaban Manual
Dengan menggunakan rumus dasar F = m . a yang dimana merupakan hukum Newton kedua. Jika gerakan kebawah dianggap merupakan gerakan positif. Pada awalnya harus mencari percepatan total karena adanya hambatan gesek Udara. Kemudian mencari rumus dasar jarak berdasarkan penurunan rumus sebelumnya.
Jawaban Menggunakan Python
Jawaban saya menggunakan python 3.7. Input fungsi yang saya masukkan berupa h =V0t + (at^2)/2 yang menjadi input fungsi python h = V0*t + (a*t**2)/2. dengan bentuk secara spesifik setelah dieksekusi sebagai berikut,
Dari perhitungan python diatas didapatkan bahwa nilai jarak sebesar 75 meter, dengan ini perhitungan manual sama dengan perhitungan python
Tugas 3
27 Februari 2020
Soal Tugas 3
Soal ini diambil dari buku ( aan Kiusalaas, Numerical Methods in Engineering with Python 3, cambridge university press )
Jawaban Menggunakan Python
Sebuah benda dipasangkan dengan sebuah pegas bernilai k. Benda tersebut diberikan gaya sebesar P(t), namun P(t) memiliki suatu kondisi.
Diberikan persamaan diferensial sebagai geraknya benda tersebut terhadap pegas. Jika diketahui massa benda adalah 2,5 kg dan k adalah 75 N/m serta tidak ada gaya gesek.
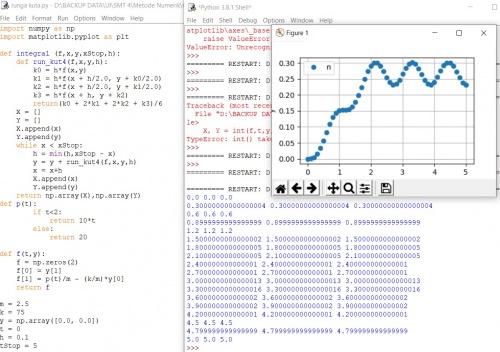
Menggunakan metode Runge-Kutta 4 orde untuk mencari perpindahannya.
Dengan metode ini, kita mendefinisikan Runge-Kutta 4 dengan k0, k1, k2, k3 dan dihitung nilai rata-rata K.
Kemudian menguraikan persamaan P(t) sesuai dengan soal. Selanjutnya penguraian persamaan diferensial benda,
sebagai persamaan turunan. kemudian untuk plotting grafik langsung oleh fungsi matplotlib.pyplot.
Sehingga hasil perhitungan tersebut adalah bentuk plot titik untuk melihat perilaku pegas terhadap benda m dengan nilai tertinggi berkisar
antara x = 2,4 detik, dengan nilai y = 0,273
Tugas 4
5 Maret 2020
Pada asistensi tanggal 3 Maret 2020, kami telah diajarakan menggunakan CFD dan perhitungan regresi linier untuk mengetahui nilai persamaan kudarat maupun persamaan biasa dari suatu persoalan berdasarkan beberapa data yang didapat.
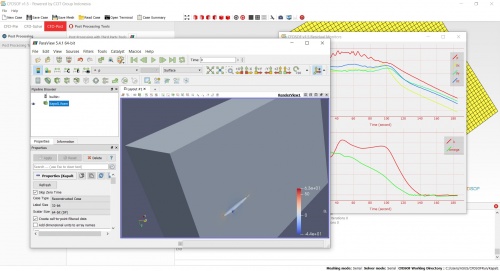
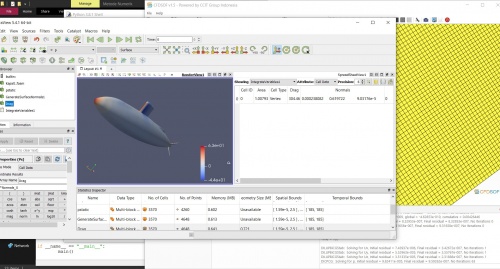
Kemudian menggunakan CFD kita menghitung hambatan uss berdasarakan pengaturan yang telah dilakukan sebelumnya, kemudian execute semua data tersebut. Dan menghasilkan, beberapa data yang ada dibawah ini.
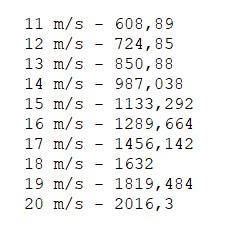
Dari gambar kedua diatas didapatkan nilai hambatan drag kapal sebesar 304,46 untuk contoh dari 5 m/s sedangkan rata - rata kecepatan kapal yang akan ada berkisar antara 11 m/s - 20 m/s. Kemudian metode tersebut diulang dari awal dengan mengubah kecepatan kapal tersebut dari 11 m/s - 20 m/s. Dan pada akhirnya didapatkan data kapal sebagai berikut.
Setelah didapatkan kemudian sepuluh data tersebut dimasukkan kedalam perhitungan menggunakan python dan didapatkan,
Dari gambar diatas didapatkan output berupa persamaan yang dicari dalam bentuk 3 angka yang akan dimasukkan kedalam persamaan kuadrat. Dan bentuk grafik dari data tersebut. Sehingga persamaan drag terhadap kecepatan yang dicari sebagai berikut,
Y= 5.05963636X² - 0.49635152x + 2.23081212
Progress Belajar - Week 3
Progress Belajar - Week 4
Asistensi Selasa, 25 Februari 2020
untuk update tugas 3 per tanggal 27 Februari 2020 23:46 di link berikut,
http://air.eng.ui.ac.id/index.php?title=Miftah_Dhia_Falah#Tugas_3
Progress Belajar - Week 5
Asistensi Selasa, 3 Maret 2020