Aisyah Aulia

Assalamu'alaikum!

Data Pribadi

Nama  : Aisyah Aulia

NPM  : 1806202260

TTL  : Jakarta, 10 Oktober 1999

Jurusan  : Teknik Perkapalan

Angkatan : 2018

email  : aisyah99auval@gmail.com

Perkenalan Singkat

Saya merupakan anak pertama dari empat bersaudara. Sejak kecil sampai sekarang, saya dan keluarga saya memiliki tempat tinggal yang berpindah-pindah. Mulai dari tinggal di beberapa pulau kecil hingga tinggal di kota-kota besar yang salah satunya adalah tempat saya melanjutkan pendidikan di perguruan tinggi impian saya ini. Oleh karena itu, hobi saya adalah jalan-jalan dan belajar mengenai banyak hal baru yang dapat memperluas pola pikir, sudut pandang, serta pengetahuan saya. Saya lebih suka belajar dari pengamatan dan pengalaman langsung dibanding membaca buku, hehe. Tidak salah jika saya dijuluki si kinestetik.

Pengalaman Pemrograman

Saya belum pernah mempelajari hal-hal yang berbau pemrograman di SMA. Mungkin ada beberapa mata kuliah yang berkaitan dan dapat diterapkan dalam pemrograman seperti kalkulus, aljabar linear, matematika teknik, dan beberapa mata kuliah cabang fisika. Alhamdulillah selama berada di bangku kuliah saya mulai mengembangkan soft skill pada penggunaan beberapa software seperti AutoCAD, Maxsurf, dan Adobe Photoshop. Saya cukup tertarik untuk mempelajari ilmu dan kemampuan pemrograman untuk mempermudah kehidupan saya bahkan orang lain kedepannya.

Garis Besar Pembelajaran

BAB 1 (Introduction to Python)

Pada bab ini diperkenalkan bahasa yang belum familiar untuk pemula pemrograman. Python merupakan orientasi bahasa yang digunakan untuk pemrograman. Python tidak seperti bahasa yang biasa digunakan dalam lingkup keteknikan, tetapi dapat dimanipulasi untuk menyelesaikan masalah keteknikan. Python memiliki beberapa kelebihan dibanding bahasa yang lain seperti :

. Terbuka, dapat digunakan untuk membuat berbagai macam program seperti CLI, aplikasi mobail, Web, IoT, Game, dan sebagainya.

. Mudah dipelajari dan mudah dipahami

. Sederhana dibanding bahasa yang lainnya

INTI PYTHON

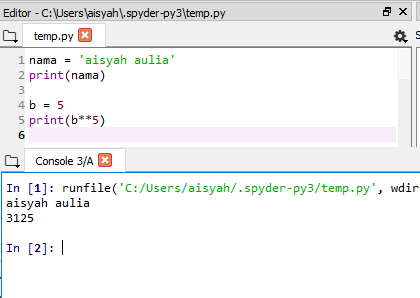
1. Variabel

alt text

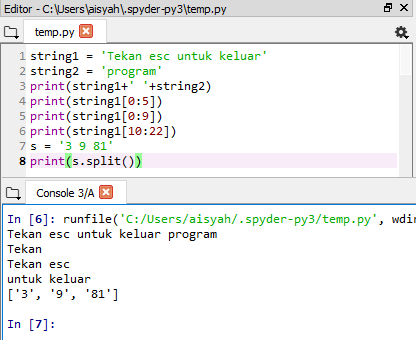
2. String

alt text

BAB 2 (System of Linear Algebraic Equations)

BAB 3 (Interpolation and Curve Fitting)

BAB 4 (Roots of Equation)

BAB 5 (Numerical Differentiation)

BAB 6 (Numerical Integration)

BAB 7 (Initial Value Problem)

BAB 8 (Two Point Boundary Value Problem)

BAB 9 (Symmetric Matrix Eigenvalue Problems)

BAB 10 (Introduction to Optimization)

Pertemuan Pertama

Pertemuan pertama pada hari Jumat, 7 Februari 2020 diperkenalkan dosen pengampu mata kuliah metode numerik Teknik Perkapalan 2019/2020 yaitu Dr. Ir. Ahmad Indra Siswantara yang biasa dipanggil Pak Dai dan Prof. Dr. Ir. Harinaldi M.Eng. Kelas pertama diisi oleh Pak Dai diawali dengan perkenalan pemrograman dengan langsung praktek membuat halaman di wiki dan bagaimana mengupload file untuk kontennya. Selain menanamkan ilmu pemrograman, Pak Dai juga memberikan nasihat agar tidak selalu bergantung pada dunia karena pengatur di muka bumi ini adalah Pencipta kita

Tugas 1 -> Menentukan nilai f(x)= x^2-1/x-1 , dengan x=1

• Tugas 1_Aisyah Aulia_1806202260

Pertemuan Kedua

Kenapa kita harus menggunakan numerik? Kenapa saat 1 dibagi 1 hasilnya 1, 2 dibagi 2 hasilnya 1, 3 dibagi 3 hasilnya 1, sedangkan 0 dibagi dengan 0 hasilnya tidak terdefinisi? Metode numerik dapat memecahkan persoalan-persoalan matematis yang rumit menjadi mudah untuk diselesaikan. Persoalan-persoalan fisika dalam berbagai bidang dapat di jadikan algoritma kalkulus.

Analisis Soal

Soal dalam buku panduan Numerical Methods in Engineering with Python yang cukup menarik buat saya adalah di soal no 20 BAB 2.

alt text

Referensi gambar : Kiusalaas, Jaan. (2013).Numerical Methods in Engineering with Python 3.Cambridge University

Di soal tersebut terdapat enam buah pegas yang disambungkan secara seri disisipi dengan lima buah balok secara selang-seling. Kedua ujung rangkaian itu juga memiliki ujung tetap yang tidak ikut berisolasi dengan pegasnya. Pada setiap pegas diketahui masing-masing konstantanya. Nah, yang menarik bagi saya disini adalah, soal tersebut biasa saya dapati dalam mata kuliah fisika mekanika dan biasa diselesaikan secara manual dengan menerapkan rumus-rumus tertentu. Pada soal ini dapat diselesaikan dengan rumus F = k . Δ x. Namun ternyata, aljabar linear dapat menjadi tools untuk menyelesaikan soal ini dengan cepat yang dikombinasikan dengan teknik pemrograman. Data-data yang kita dapat dari soal dapat dijadikan persamaan dari balok dan pegas yang bekerja pada sistem. Contoh persamaan pertama 3(x2-x1) - 2x1 = -80

   F12 = k2.x2 - k12.x1 - k1.x1         ; dengan asumsi arah gaya ke kanan
   -80 = 3x2 - 3x1 - 2x1

Persamaan-persamaaan ini kemudian dapat diselesaikan dengan membentuk matriksnya dan dilanjutkan dengan metoda numerik

Tugas 2 -> Pembahasan analisis soal

Solusi manual

Pada penyelesaian secara manual, saya menggunakan metode crammer untuk mencari nilai x nya. Langkah- langkah pengerjaannya adalah dengan membuat SPL terlebih dahulu, kemudian SPL-SPL tersebut dijadikan matrix sehingga mempermudah pengerjaan. Lalu dari matrix yang didapat kita dapat mengganti setiap kolom pada matrix A dengan kolom matrix B yang kemudian didapat setiap nilai x sesuai pada setiap kolom yang diganti, misal untuk mencari nilai x1, kolom 1 diganti dengan kolom matix B, dan seterusnya seperti pada gambar :

alt text

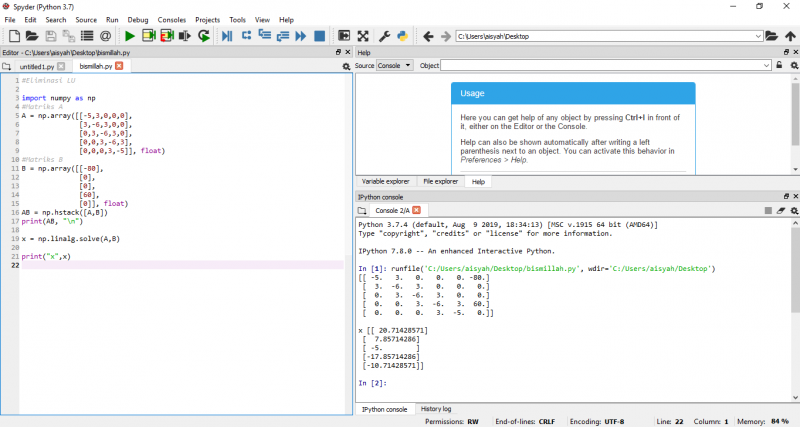
Solusi menggunakan aplikasi Spyder(Python 3.7)

Pada penyelesaian menggunakan aplikasi coding, saya menggunakan matrix yang telah disusun tadi dengan numpy yang merupakan komputasi produk array. Dengan matrix 5x5 yang diselesaikan cukup lama dengan manual, menggunakan aplikasi coding mempermudah penyelesaiannya dalam waktu singkat dengan resiko kesalahan hitung yang kecil. Berikut penyelesaiannya dengan aplikasi :

alt text

Tugas 2 -> Initial Value Problem

Solusi Manual

Pada solusi manual, saya menggunakan rumus pokok F = m.a yang merupakan hukum kedua newton dengan mempertimbangkan gaya yang bekerja pada penerjun adalah gaya beratnya yang membawanya turun kebawah dan gaya hambat udara yang merupakan pengaruh gerak angin terhadap parasut. Asumsi penyelesaian adalah positif untuk semua arah yang mengarah ke bawah(sesuai dengan gerak jatuh penerjun). Kemudian setelah didapat percepatan yang dialami oleh penerjun, saya menghitung ketinggian yang ditanya terhadap waktu yang telah ditentukan untuk mencapai tanah. Rumus ketinggian h = V0t + at²/2 merupakan bagian dari fungsi jarak terhadap waktu xt = x0 + V0t + at²/2 yang merupakan turunan dari fungsi kecepatan v = dx/dt. Maka saya menyimpulkan soal ini merupakan tipe soal initial value problem. Berikut penyelesaian secara manualnya :

alt text

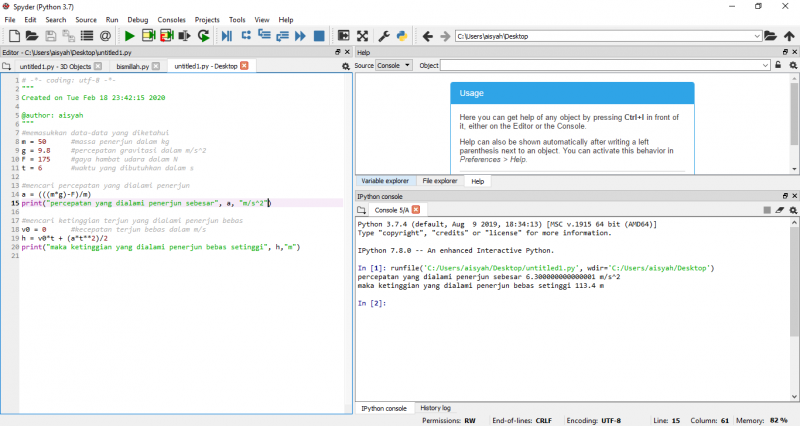
Solusi Menggunakan Aplikasi

Pada solusi dengan aplikasi Spyder(Python3.7) saya menginput data-data yang diketahui di soal, kemudian membuat rumusnya, dan mendapatkan percepatan yang dicari. Setelah percepatan didapat, saya menghitung ketinggian yang dicari dengan menginput rumus juga h = V0t + at²/2 dengan kode h = v0*t + (a*t**2)/2 dan kemudian memasukkan kode print("maka ketinggian yang dialami penerjun bebas setinggi", h,"m"). Lalu didapat ketinggian penerjun hingga sampai ke tanah. Berikut penyelesaiannya :

alt text

Pada aplikasi ini saya sebatas mencari nilai-nilai yang diinginkan, belum secara spesifik mendapat nilai di titik-titik sesaat.

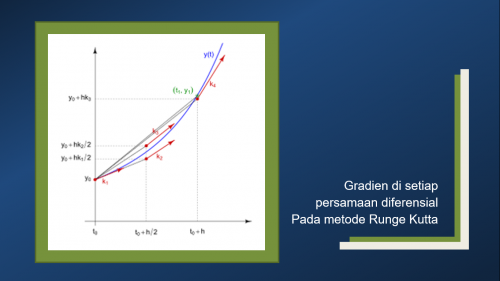
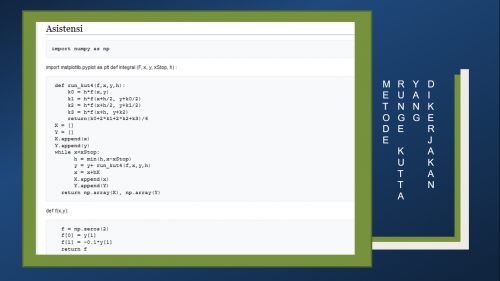
PPT Progres Belajar Metoda Numerik

alt text

Metoda numerik merupakan mata kuliah yang berhubungan erat dengan pemrograman. Metoda numerik memanipulasi data dan memanfaatkan bahasa program untuk menyelesaikan suatu permasalahan matematis.

alt text

alt text

Pertemuan Ketiga

Setiap manusia punya frekuensinya sendiri. Contohnya suara. Suara ditimbulkan oleh getaran pita suara. Pita suara membuat udara memiliki fluktuasi tekanan yang bergerak osilasi sehingga menghasilkan beberapa periode yang berulang. Ada sebuah pegas yang kita tarik sepanjang ∆x sehingga kembali naik ke atas karena mempunyai kelembaman dan kembali ke bawah karena mempunyai berat. Hal ini dapat disusun model matematika nya secara metode numerik. Kedepannya dapat mensimulasikan hidrodinamika kapal dan memodelkan dinamika geraknya. Dengan menggunakan simulasi software Computational Fluid Dynamics (CFD). Kita akan melihat terjadinya hambatan yang merupakan fungsi dari kecepatan dengan metode regresi dan bisa melakukan optimasi bentuk. Pada pertemuan kali ini juga dibahas sedikit tentang kesetimbangan energi. Dimana massa dalam suatu sistem adalah tetap artinya tidak bisa diciptakan dan dimusnahkan. Ini membutuhkan ilmu kalkulus. Dengan merujuk persamaan dM/dt = 0 yang merupakan prinsip konservasi massa.

Ada tiga prinsip dasar ilmu teknik :

1. Prinsip konservasi massa. v x A = Q= konstan , tetapi rumus ini terbatas. aliran inkompresibel adalah aliran yang massa jenisnya tidak berubah.

2. Prinsip konservasi momentum. Sering disebut kesetimbangan gaya. F=m.a -> F=M.(dv/dt)

3. Prinsip konservasi energi. dE/dt = W + Q atau laju perubahan energi. Dalam suatu sistem ada resultan gaya maka sistem itu memiliki percepatan

Asistensi dan Tugas

- Kode Pertama yang saya kerjakan
import numpy as np
import matplotlib.pyplot as plt
def integral (F, x, y, xStop, h) :
  def run_kut4(f,x,y,h):
      k0 = h*f(x,y)
      k1 = h*f(x+h/2, y+k0/2)
      k2 = h*f(x+h/2, y+k1/2)
      k3 = h*f(x+h, y+k2)
      return(k0+2*k1+2*k2+k3)/6
  X = []
  Y = []
  X.append(x)
  Y.append(y)
  while x<xStop:
        h = min(h,x-xStop)
        y = y+ run_kut4(f,x,y,h)
        x = x+hX
        X.append(x)
        Y.append(Y)
    return np.array(X), np.array(Y)
def f(x,y):
    f = np.zeros(2)
    f[0] = y[1]
    f[1] = -0.1*y[1]
    return f
h= 0.2
x= 0
y= [0,1]
xStop=1
X,Y = integral(f,x,y, xStop,h)
plt.plot(X,Y[;,1],' ',c=pink')
plt.show()

• pada kode ini saya belum mendapatkan hasil karena aplikasi yang saya gunakan tidak memiliki modul runge kutta

- Kode Kedua
x0 = 0
y = 0
h = 0
x = float(input("masukkan nilai t: "))
if 0<= x < 2:
  def dydx(x,y):
    return (4*x- 30*y)
    def rungekutta(x0, y0, x, h):
      n= (int)((x-x0)/h)
      y= y0
      for i in range(1, n+1)
          k1 = h*dydx(x0,y)
          k2 = h*dydx(x0+0.5*h, y+0.5*k1)
          k3 = h*dydx(x0+0.5*h,y+0.5*k2)
          k4 = h*dydx(x0+h, y+k3)
          y = y+(1/6)*(k1+2k2+2k3+k4)
          x0 = xO+h
      return y
    print("Nilai y pada t=", x, "yaitu", rungekutta(x0,y,x,h))
elif x >=2:
  def dydx(x,y):
    return(8-30*y)
  def rungekutta(x0,y0,x,h):
    n = (int)((x-x0)/h)
    y = y0
    for i in range(1, n+1)
         k1 = h*dydx(x0,y)
         k2 = h*dydx(x0+0.5*h, y+0.5*k1)
         k3 = h*dydx(x0+0.5*h,y+0.5*k2)
         k4 = h*dydx(x0+h, y+k3)
         y = y+(1/6)*(k1+2k2+2k3+k4)
         x0 = xO+h
    return y
  print("y saat t=",x, "yaitu", rungekutta(x0,y,x,h))

hasil :
nilai y pada t= 2 yaitu 0.26666666666665745
nilai y pada t= 3 yaitu 0.26666666666665745
nilai y pada t= 4 yaitu 0.26666666666665745
nilai y pada t= 5 yaitu 0.06222223581783385
nilai y pada t= 6 yaitu 0.07554222229010824
nilai y pada t= 7 yaitu 0.0888755555892813

Hasil Asistensi

alt text

alt text

alt text

alt text

alt text

alt text