Difference between revisions of "Tugas 1 Alpha Roissul"
| Line 7: | Line 7: | ||
[[File:Metode_Manual.jpeg|300px|thumb|center|Metode Manual]] | [[File:Metode_Manual.jpeg|300px|thumb|center|Metode Manual]] | ||
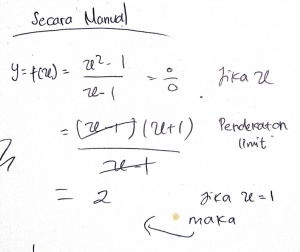
| − | Penyelesaian dengan menggunakan metode menghitung langsung cukup membingungkan karena jika dihitung dengan metode biasa akan menghasilkan 0/0 (tidak terdefinisi) jika x= 1. Maka dari itu dicari dengan cara lain yaitu | + | Penyelesaian dengan menggunakan metode menghitung langsung cukup membingungkan karena jika dihitung dengan metode biasa akan menghasilkan 0/0 (tidak terdefinisi) jika x= 1. Maka dari itu dicari dengan cara lain menggunakan metode limit namun sebelum menggunakan metode ini saya pribadi coba menggunakan cara penurunan namun kemungkinan besar saya salah melakukan kalkulasi dan mendapatkan hasil yang sama yaitu 0/0. Oleh karena itu saya memutuskan untuk lanjut menggunakan metode limit dan memperoleh hasil sebesar 2 |
== Metode Software == | == Metode Software == | ||
| Line 14: | Line 14: | ||
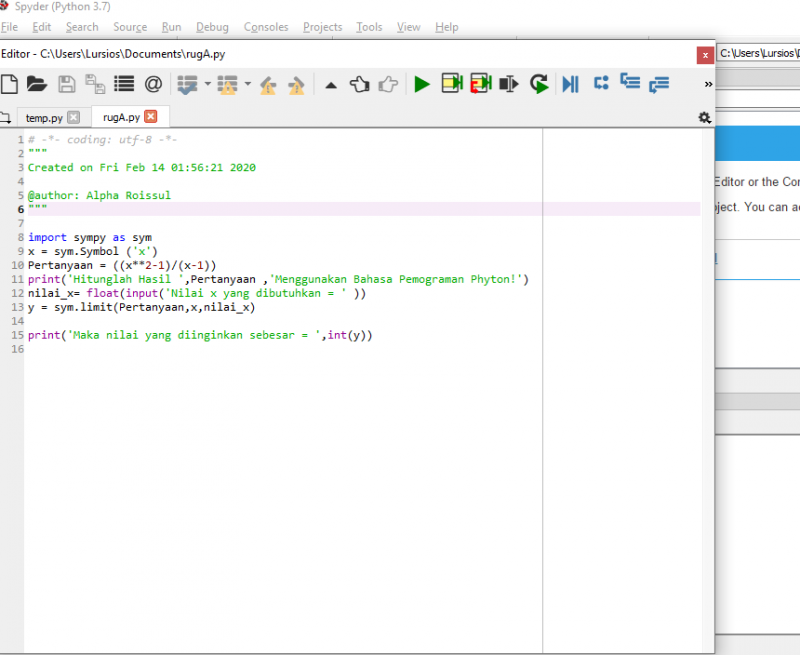
Pada software ini saya menggunakan sympy (Symbolic Pyhton) untuk menyelesaikan limit yang terdapat pada soal. Terdapat langkah langkah yang harus dilakukan seperti mendefinisikan nilai x, memasukan f(x) ke dalam softwarenya, memasukan nilai x, memasukan jawaban dari limit kedalam soal, dan menentukan output dari soalnya sehingga ada jawaban. | Pada software ini saya menggunakan sympy (Symbolic Pyhton) untuk menyelesaikan limit yang terdapat pada soal. Terdapat langkah langkah yang harus dilakukan seperti mendefinisikan nilai x, memasukan f(x) ke dalam softwarenya, memasukan nilai x, memasukan jawaban dari limit kedalam soal, dan menentukan output dari soalnya sehingga ada jawaban. | ||
| + | |||
| + | Butuh waktu yang cukup lama untuk mengerjakan tugas ini tanpa bimbingan karena di phyton idle secara sendirinya tidak dapat melakukan kalkulasi yang di inginkan dan tanpa mengimport symp kemungkinan besar tugas ini tidak akan terselesaikan hahahaha. | ||
[[File:Gece 2.png|800px|thumb|center|Metode Software]] | [[File:Gece 2.png|800px|thumb|center|Metode Software]] | ||
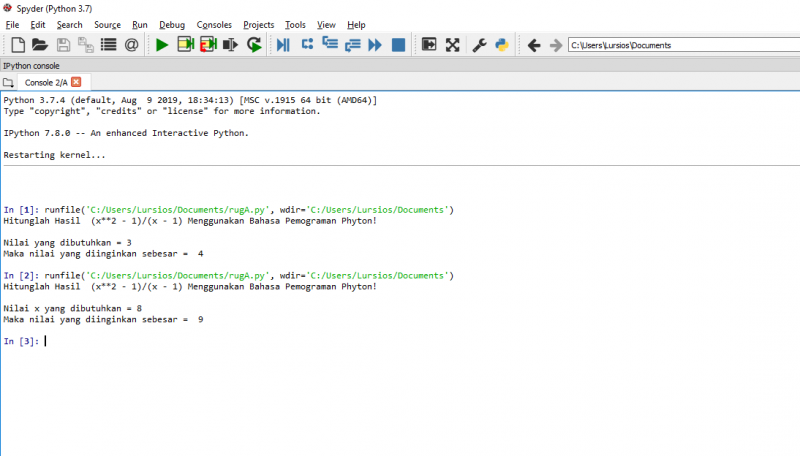
| − | + | setelah dilakukan permodelan maka akan didapatkan hasil dari perhitungan yang sudah dilakukan dengan menekan F5 dan didapatkan hasilnya adalah 2, sama dengan perhitungan manual. Bisa juga mendapatkan value x yang variatif dengan persamaan yang sama dengan penginputan saja. | |
== Analisis dan Komentar == | == Analisis dan Komentar == | ||
| − | Perhitungan matematika sering kali membuat kita harus berpkir lebih bagaimana cara menyelesaikannya. | + | Perhitungan matematika sering kali membuat kita harus berpkir lebih bagaimana cara menyelesaikannya. Dengan menggunakan metode software terbukti kalau awal permodelan dan pemrograman akan memakan waktu yang cukup lama jika tidak mengerti dasaran dari programming namun ketika sudah mulai mengerti dan paham bisa dikatakan bahwa hal ini diciptakan cocok untuk orang orang malas seperti saya. |
Latest revision as of 03:24, 14 February 2020
Tugas 1 (Pertama)
Tentukan F(x)=(x^2-1/(x-1) dari F(1)menggunakan metode manual dan menggunakan software pada komputer kemudian dianalisa dan diberikan komentar
Metode Manual
Penyelesaian dengan menggunakan metode menghitung langsung cukup membingungkan karena jika dihitung dengan metode biasa akan menghasilkan 0/0 (tidak terdefinisi) jika x= 1. Maka dari itu dicari dengan cara lain menggunakan metode limit namun sebelum menggunakan metode ini saya pribadi coba menggunakan cara penurunan namun kemungkinan besar saya salah melakukan kalkulasi dan mendapatkan hasil yang sama yaitu 0/0. Oleh karena itu saya memutuskan untuk lanjut menggunakan metode limit dan memperoleh hasil sebesar 2
Metode Software
Pada software ini saya menggunakan sympy (Symbolic Pyhton) untuk menyelesaikan limit yang terdapat pada soal. Terdapat langkah langkah yang harus dilakukan seperti mendefinisikan nilai x, memasukan f(x) ke dalam softwarenya, memasukan nilai x, memasukan jawaban dari limit kedalam soal, dan menentukan output dari soalnya sehingga ada jawaban.
Butuh waktu yang cukup lama untuk mengerjakan tugas ini tanpa bimbingan karena di phyton idle secara sendirinya tidak dapat melakukan kalkulasi yang di inginkan dan tanpa mengimport symp kemungkinan besar tugas ini tidak akan terselesaikan hahahaha.
setelah dilakukan permodelan maka akan didapatkan hasil dari perhitungan yang sudah dilakukan dengan menekan F5 dan didapatkan hasilnya adalah 2, sama dengan perhitungan manual. Bisa juga mendapatkan value x yang variatif dengan persamaan yang sama dengan penginputan saja.
Analisis dan Komentar
Perhitungan matematika sering kali membuat kita harus berpkir lebih bagaimana cara menyelesaikannya. Dengan menggunakan metode software terbukti kalau awal permodelan dan pemrograman akan memakan waktu yang cukup lama jika tidak mengerti dasaran dari programming namun ketika sudah mulai mengerti dan paham bisa dikatakan bahwa hal ini diciptakan cocok untuk orang orang malas seperti saya.