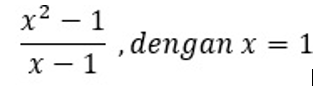Difference between revisions of "Tugas 1 Fadillah Nurrani"
| Line 2: | Line 2: | ||
== Tugas Mencari limit dari nilai yang ditentukan == | == Tugas Mencari limit dari nilai yang ditentukan == | ||
| − | Pada hari Jumat, 7 Februari 2020, Pak Dai mengajar pada kelas Metode Numerik, dan menugaskan mahasiswa kelas untuk mengerjakan soal yang diberikan, secara manual dan juga menggunakan | + | Pada hari Jumat, 7 Februari 2020, Pak Dai mengajar pada kelas Metode Numerik, dan menugaskan mahasiswa kelas untuk mengerjakan soal yang diberikan, secara manual dan juga menggunakan pendekatan metode numerik. Saya memilih untuk menggunakan aplikasi '''''python ‘spyder’''''' menggunakan bantuan '''sympy''' untuk memudahkan pengerjaan dengan limit. |
Soal yang diberikan Pak Dai adalah: | Soal yang diberikan Pak Dai adalah: | ||
| Line 17: | Line 17: | ||
Saat saya mengerjakan soal diatas menggunakan metode manual, didapatkan hasil yaitu f(x) = 2, dengan menggunakan cara limit. | Saat saya mengerjakan soal diatas menggunakan metode manual, didapatkan hasil yaitu f(x) = 2, dengan menggunakan cara limit. | ||
| − | Untuk mengoreksi hasil yang telah saya dapatkan, saya mencoba menghitung soal diatas menggunakan | + | Untuk mengoreksi hasil yang telah saya dapatkan, saya mencoba menghitung soal diatas menggunakan pendekatan metode numerik. Aplikasi yang saya gunakan adalah '''''python ‘spyder’''''' dengan bantuan '''sympy'''. |
| Line 46: | Line 46: | ||
[[File:Nugasyok.PNG]] | [[File:Nugasyok.PNG]] | ||
| + | |||
| + | Jika dilihat pada persamaan diatas, saya mendefinisikan soal diatas menjadi f(x) = f(x)/g(x) dimana f(X) = (x^2-1) dan g(x) = (x-1). Setelah itu barulah nilai x dimasukan ke persamaan. Dikarenakan mengatasi masalah jika terjadi pembagian 0/infinity (tidak terdefinisi), maka dari itu digunakan limit dengan bantuan '''sympy''', sehingga hanya tinggal ditambahkan nilai x yang diinginkannya. Didapatkan hasil yaitu 2, sesuai berikut: | ||
[[File:Metnumyok.PNG]] | [[File:Metnumyok.PNG]] | ||
| − | == | + | Pada soal diatas nilai x yang diinginkan adalah 1, namun untuk memastikan bahwa algoritma yang dimasukan benar, maka dari saya mencoba memasukan nilai lain yaitu x = 3, didapatkan hasil: |
| + | |||
| + | [[File:Metnum3.PNG]] | ||
| + | |||
| + | Didapatkan hasil bahwa apabila x = 3, maka jawabannya adalah 4, sehingga algoritma nya benar. | ||
| + | |||
| + | [[File:Metnumnih.PNG]] | ||
| + | |||
| + | == Kesimpulan == | ||
| + | Menurut saya pribadi, menggunakan aplikasi coding sangat membantu apabila diinginkan nilai nilai yang berjumlah besar dan sulit, namun untuk penyelesaian yang mudah, lebih enak memakai metode manual. Saya senang bisa belajar hal baru seperti coding ini, awalnya saya sempat ragu untuk menyelesaikan tugsa ini, namun akhirnya setelah belajar melalui internet dan diajarkan oleh teman, saya jadi menyukai aplikasi coding. | ||
| + | |||
| + | Terimakasih. | ||
Latest revision as of 00:07, 14 February 2020
Contents
Tugas Mencari limit dari nilai yang ditentukan
Pada hari Jumat, 7 Februari 2020, Pak Dai mengajar pada kelas Metode Numerik, dan menugaskan mahasiswa kelas untuk mengerjakan soal yang diberikan, secara manual dan juga menggunakan pendekatan metode numerik. Saya memilih untuk menggunakan aplikasi python ‘spyder’ menggunakan bantuan sympy untuk memudahkan pengerjaan dengan limit.
Soal yang diberikan Pak Dai adalah:
Pertanyaan: Berapakah f(x) apabila x=1?
Menggunakan Metode Manual
Saat saya mengerjakan soal diatas menggunakan metode manual, didapatkan hasil yaitu f(x) = 2, dengan menggunakan cara limit.
Untuk mengoreksi hasil yang telah saya dapatkan, saya mencoba menghitung soal diatas menggunakan pendekatan metode numerik. Aplikasi yang saya gunakan adalah python ‘spyder’ dengan bantuan sympy.
Menggunakan Metode Numerik
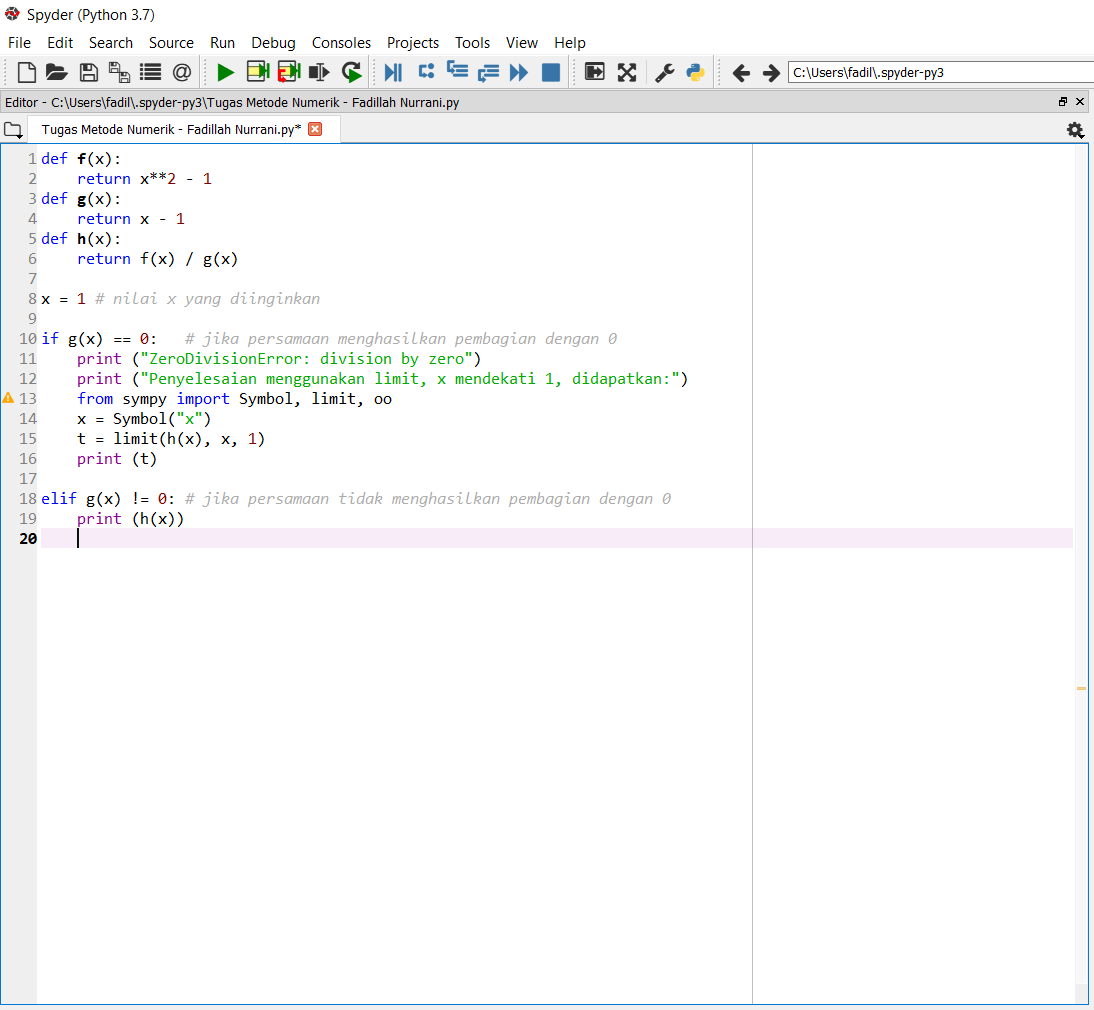
Menggunakan aplikasi python ‘spyder’, saya memasukan algoritma yang dibutuhkan untuk menghasilkan fungsi diatas. Algoritma yang saya pakai adalah:
def f(x):
return x**2 - 1
def g(x):
return x - 1
def h(x):
return f(x) / g(x)
x = 1 # nilai x yang diinginkan
if g(x) == 0: # jika persamaan menghasilkan pembagian dengan 0
print ("ZeroDivisionError: division by zero")
print ("Penyelesaian menggunakan limit, x mendekati 1, didapatkan:")
from sympy import Symbol, limit, oo
x = Symbol("x")
t = limit(h(x), x, 1)
print (t)
elif g(x) != 0: # jika persamaan tidak menghasilkan pembagian dengan 0
print (h(x))
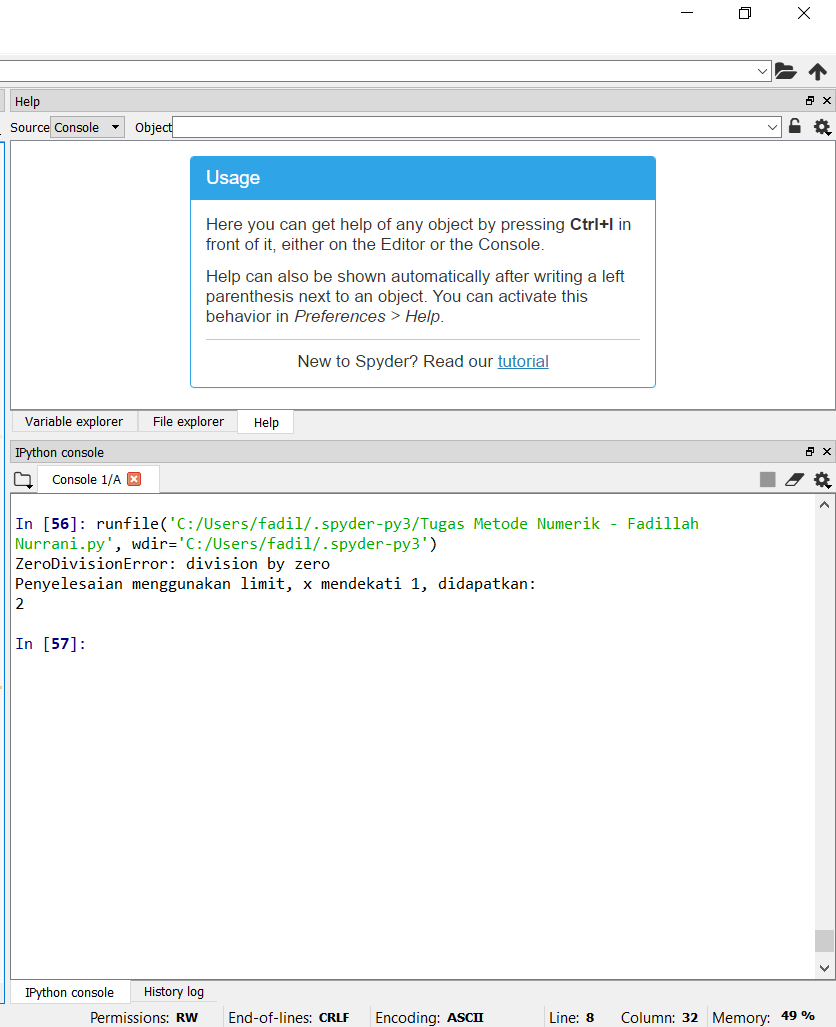
Jika diaplikasikan pada python ‘spyder’, didapatkan:
Jika dilihat pada persamaan diatas, saya mendefinisikan soal diatas menjadi f(x) = f(x)/g(x) dimana f(X) = (x^2-1) dan g(x) = (x-1). Setelah itu barulah nilai x dimasukan ke persamaan. Dikarenakan mengatasi masalah jika terjadi pembagian 0/infinity (tidak terdefinisi), maka dari itu digunakan limit dengan bantuan sympy, sehingga hanya tinggal ditambahkan nilai x yang diinginkannya. Didapatkan hasil yaitu 2, sesuai berikut:
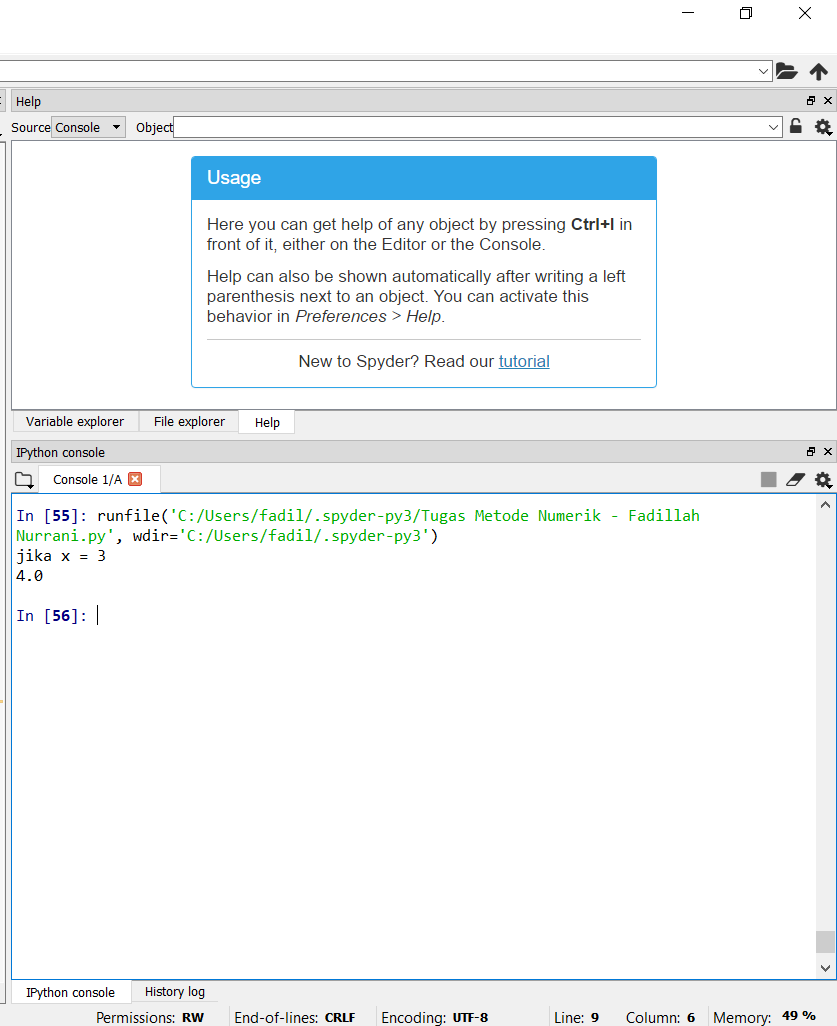
Pada soal diatas nilai x yang diinginkan adalah 1, namun untuk memastikan bahwa algoritma yang dimasukan benar, maka dari saya mencoba memasukan nilai lain yaitu x = 3, didapatkan hasil:
Didapatkan hasil bahwa apabila x = 3, maka jawabannya adalah 4, sehingga algoritma nya benar.
Kesimpulan
Menurut saya pribadi, menggunakan aplikasi coding sangat membantu apabila diinginkan nilai nilai yang berjumlah besar dan sulit, namun untuk penyelesaian yang mudah, lebih enak memakai metode manual. Saya senang bisa belajar hal baru seperti coding ini, awalnya saya sempat ragu untuk menyelesaikan tugsa ini, namun akhirnya setelah belajar melalui internet dan diajarkan oleh teman, saya jadi menyukai aplikasi coding.
Terimakasih.