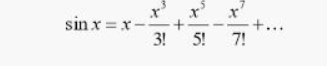Difference between revisions of "Hario Gibran"
Hario.gibran (talk | contribs) |
Hario.gibran (talk | contribs) |
||
| Line 25: | Line 25: | ||
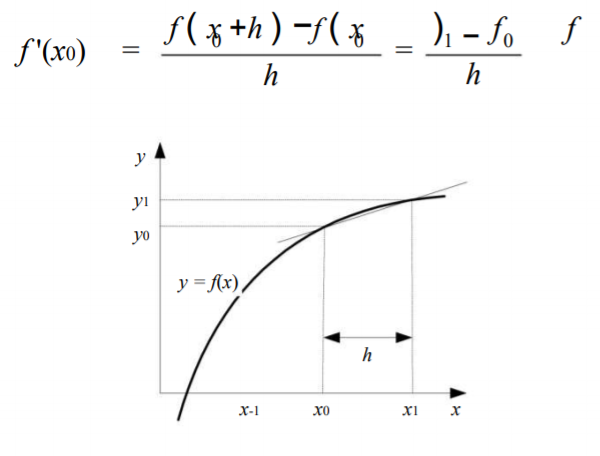
1. Turunan maju, | 1. Turunan maju, | ||
| − | + | [[File:Turunan maju 1706036362.PNG]] | |
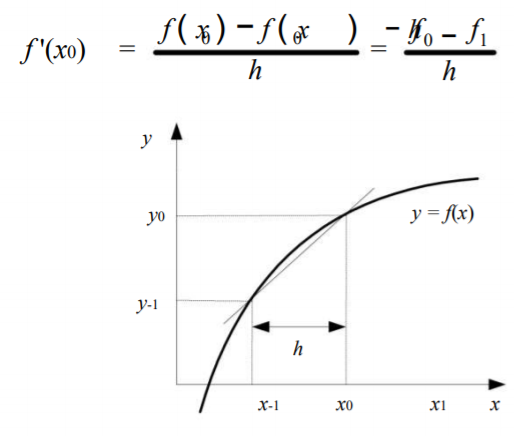
2. Turunan mundur, | 2. Turunan mundur, | ||
| − | + | [[File:Turunan mundur 1706036362.PNG]] | |
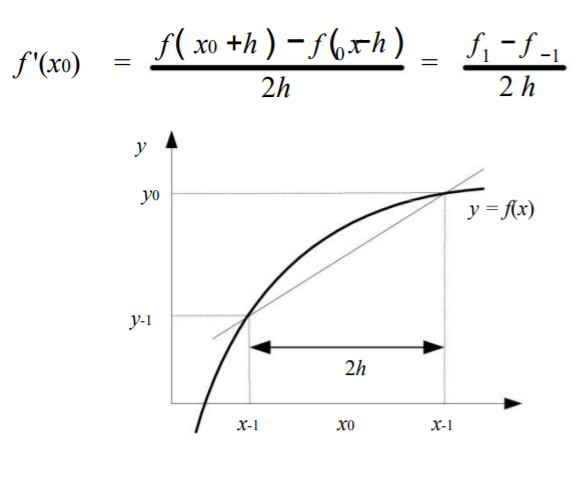
3. Turunan pusat | 3. Turunan pusat | ||
| + | [[File:Turunan pusat 1706036362.PNG]] | ||
Revision as of 11:53, 17 December 2019
Contents
[hide]Profil
- Nama : Hario Gibran
- NPM : 1706036362
Pertemuan ke-1, 3 September 2019
Oleh : Dr. Ahmad Indra Siswantara dan Dr. Engkos Achmad Kosasih Pada pertemuan pertama mata kuliah metode numerik, kami dijelaskan bahwa banyak penyelesaian matematik dapat diselesaikan dengan menggunakan teknik metode numerik. Karena tidak semua permasalahan matematik dapat diselesaikan menggunakan kalkulator yang sederhana, maka digunakan metode numerik.
Untuk mendapat nilai log x, ln(x+2), atau ln(x) perlu proses yang panjang dan rumit jika dilakukan secara manual. Untuk mempermudah hal tersebut, ilmu yang dipelajari dalam metode numerik yaitu Deret Taylor atau Deret MacLaurin.
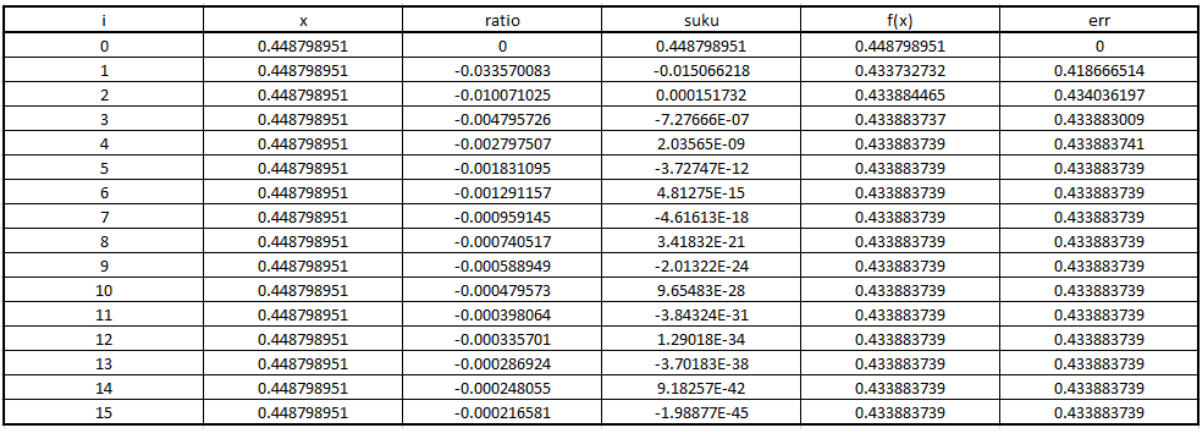
Pada pertemuan kali ini, kami mahasiswa ditugaskan untuk mencari nilai dari sin(pi/7). Berikut penyelesaiannya :
Pertemuan ke-2, 10 September 2019
Pada pertemuan kali ini, mahasiswa diberi penjelasan tentang pseudocode. Pada dasarnya, pseudocode merupakan suatu bahasa yang memungkinkan programmer untuk berpikir terhadap permasalahan yang harus dipecahkan tanpa harus memikirkan syntax dari bahasa pemrograman yang tertentu. Tidak ada aturan penulisan syntax di dalam pseudocode. Jadi pseudocode digunakan untuk menggambarkan logika urut-urutan dari program tanpa memandang bagaimana bahasa pemrogramannya.
Lalu pada pertemuan ini kami diminta membuat pseudocode untuk menemukan nilai dari sin(x), cos(x), dan e^x.
Pertemuan ke-3, 17 September 2019
Pada pertemuan kali ini diberi penjelasan mengenai turunan numerik. Persoalan turunan numerik ialah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Dijelaskan juga bahwa ada 3 pendekatan dalam menghitung turunan numerik, diantaranya: