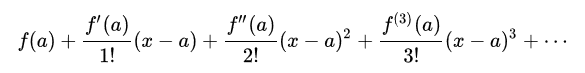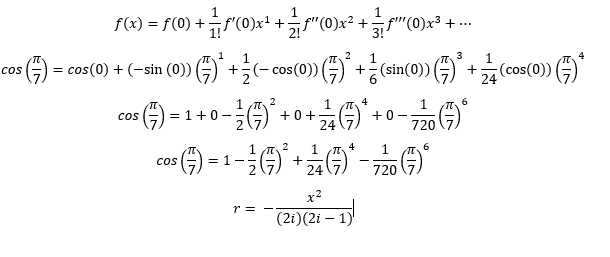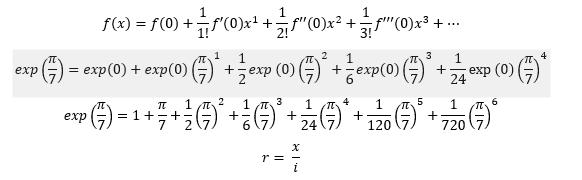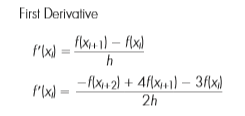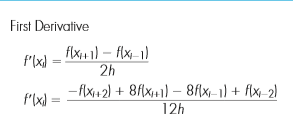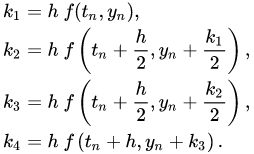Difference between revisions of "Bintang Farhan Muhammad"
(→Artificial Neural Network untuk Regresi Plot Grafik Lift-to-Drag Ratio, Selasa 12 November 2019:) |
(→Melakukan Optimasi Lift-to-Drag Ratio dengan Simulasi CFDSOF-NG, Selasa 12 November 2019:) |
||
| Line 164: | Line 164: | ||
[[File:CFD3.PNG]] [[File:CFD4.PNG]] [[File:CFD5.PNG]] | [[File:CFD3.PNG]] [[File:CFD4.PNG]] [[File:CFD5.PNG]] | ||
| − | == '''Melakukan Optimasi Lift-to-Drag Ratio dengan Simulasi CFDSOF-NG, Selasa | + | == '''Melakukan Optimasi Lift-to-Drag Ratio dengan Simulasi CFDSOF-NG, Selasa 19 November 2019:''' == |
| + | Optimasi merupakan proses mencari nilai maksimum atau minimum dari sebuah kurva yang diberikan. Cara termudah dari optimasi tentu dengan menurunkan satu kali lalu hasil turunan tersebut disamadengankan dengan nol. Tetapi tidak selalu semudah itu, seringkali optimasi dilakukan dengan banyak Batasan, hal inilah yang kita sebut constrained optimization. Pada kesempatan kali ini, saya berkesempatan melakukan optimasi lift-to-drag ratio pada sebuah airfoil. | ||
| + | |||
| + | Lift-to-drag ratio merupakan sebuah rasio antara lift force dan drag force. Parameter ini menjadi penting karena kita tentu ingin mencari flight condition terbaik untuk sebuah pesawat dimana dibutuhkan thrust seminimal mungkin untuk mendapatkan lift yang besar dan drag sekecil mungkin, yang bisa kita dapatkan pada nilai lift-to-drag ratio paling besar. Langkah-langkah dalam tugas ini sebagai berikut. | ||
| + | |||
| + | 1) Melakukan pemodelan dengan CAD (Inventor) atau download pada GrabCAD dan di-export dalam format .stl | ||
| + | |||
| + | 2) Di-import ke CFDSOF-NG dan lakukan simulasi. Kali ini tidak hanya mencari drag force tetapi juga lift force. | ||
| + | |||
| + | 3) Lakukan plot lift force, plot drag force, dan plot lift-to-drag ratio | ||
| + | |||
| + | 4) Untuk masing-masing scatter plot perhatikan trendnya, apakah linear atau polynomial | ||
| + | |||
| + | 5) Lakukan regresi sesuai dengan hasil scatter plot | ||
| + | |||
| + | 6) Setelah dilakukan regresi, lakukan optimasi | ||
| + | |||
| + | Pada kesempatan kali ini didapatkan trend grafik paling mendekati fungsi polynomial pangkat enam sehingga dilakukan regresi pangkat enam. Saya mencoba melakukannya dengan tiga metode, 1) Multiple Linear Regression dengan nilai x1 = x^1, x2 = x^2, dst. 2) Polynomial Regression untuk polynomial pangkat enam, 3)Excel. Karena untuk metode pertama dan kedua penyelesaiannya dengan matriks dan harus dilakukan eliminasi Gauss-Jordan, maka saya melakukan coding dalam Bahasa Python untuk melakukan hal tersebut. | ||
== '''Artificial Neural Network untuk Regresi Plot Grafik Lift-to-Drag Ratio, Selasa 3 Desember 2019:''' == | == '''Artificial Neural Network untuk Regresi Plot Grafik Lift-to-Drag Ratio, Selasa 3 Desember 2019:''' == | ||
Revision as of 14:04, 15 December 2019
Bismillahirrahmanirrahim
Assalamualaikum wr wb
"Sebaik-baik manusia adalah yang bermanfaat bagi orang lain" (HR. Ahmad)
Contents
- 1 Profil:
- 2 Metode Numerik, Deret Taylor, & Deret Maclaurin, Selasa 3 September 2019:
- 3 Tingkatan Bahasa Komputer, Contoh Pseudocode, Selasa 10 September 2019:
- 4 Turunan Numerik, Selasa 17 September 2019:
- 5 Secant Method, Bisect Method, dan Newton Raphson Method, Selasa 24 September 2019:
- 6 Truncation Error, Rounding Error, Persamaan Banyak, Selasa 1 Oktober 2019:
- 7 PR Pemodelan Matematika dari Kecepatan Maksimal Mobil, dan Pseudocode untuk Penyelesaiannya, Selasa 29 Oktober 2019:
- 8 Menghitung Drag dengan CFDSOF-NG, Regresi Gaya Drag, dan Perhitungan Transient Response dari Fungsi Kecepatan Maksimum Mobil, Selasa 5 November 2019:
- 9 Melakukan Optimasi Lift-to-Drag Ratio dengan Simulasi CFDSOF-NG, Selasa 19 November 2019:
- 10 Artificial Neural Network untuk Regresi Plot Grafik Lift-to-Drag Ratio, Selasa 3 Desember 2019:
Profil:
Perkenalkan nama saya Bintang Farhan Muhammad, saya biasa dipanggil Bintang. Saya merupakan salah satu murid di kelas Metode Numerik 01.
NPM : 1706986334
Jurusan : Teknik Mesin
Metode Numerik, Deret Taylor, & Deret Maclaurin, Selasa 3 September 2019:
Metode Numerik
Sebuah fungsi terkadang tidak selalu dapat dicari nilai dari akar-akarnya dengan perhitungan sederhana. Untuk persamaan dua variable kita dapat menggunakan rumus AB, untuk 3 variable dapat menggunakan rumus ABC. Untuk 4 variable dan seterusnya, cukup sulit untuk menemukan nilai dari akar-akar secara manual. Untuk itu dapat digunakan metode numerik sebagai salah satu cara mengaproksimasi nilai tersebut. Metode numerik salah satu contohnya adalah Newton-Raphson dan Euler. Cara metode numerik menggunakan perhitungan yang berulang-ulang sehingga hampir tidak mungkin untuk dilakukan perhitungan secara manual, maka dari itu dibutuhkan bantuan dari computer agar perhitungan dapat dilakukan dengan hasil yang teliti dan akurat.
Deret Taylor & Maclaurin
Deret Taylor merupakan sebuah deret polynomial dari sebuah fungsi, untuk mengaproksimasikan nilai fungsi tersebut. Jika nilai acuan dari deret Taylor (a) bernilai 0, maka deret tersebut akan menjadi deret Maclaurin. Kedua deret ini fungsinya sama, untuk mencari nilai aproksimasi dari suatu fungsi.
Untuk membuat sebuah program metode numerik yang baru memiliki kali, bagi, tambah, dan kurang, perlu ditemukan sebuah pola dari deret tersebut.
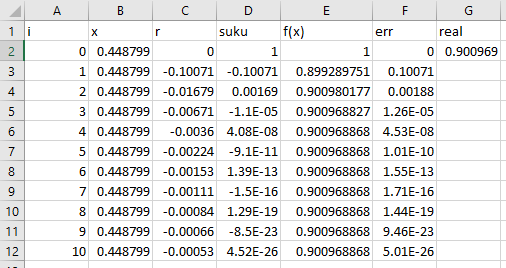
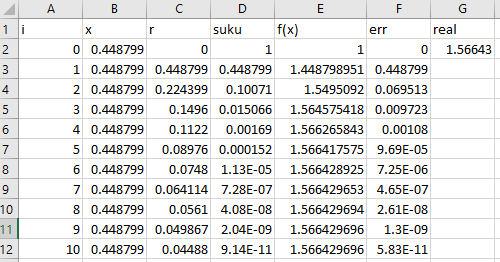
Akan diberikan contoh aproksimasi cos(x) dan e^x dengan nilai x = pi/7, dilakukan dengan deret Maclaurin dengan menggunakan Microsoft Excel.
1) cos(pi/7) dengan deret Maclaurin
2) e^(pi/7) dengan deret Maclaurin
Tingkatan Bahasa Komputer, Contoh Pseudocode, Selasa 10 September 2019:
Tingkatan bahasa computer yang paling rendah adalah binary, atau bisa juga disebut bahasa mesin. Dalam system binary hanya ada angka 1 dan 0. Bahasa mesin sangat sulit dipelajari karena sangat banyak kombinasi angkanya. Akhirnya dibuatlah bahasa penerjemah yang lebih mudah dibaca oleh manusia, kemudian di computer akan diterjemahkan lagi ke bahasa mesin/binary, yang biasa kita sebut dengan compiler. Compiler merupakan penerjemah yang sudah dapat bisa di-running oleh computer. Berbeda dengan pseudocode, pseudocode merupakan bahasa atau program yang tidak bisa diterjemahkan karena tidak ada compiler yang bisa menerjemahkan ke bahasa computer. Dibawah ini contoh pseudocode untuk beberapa fungsi.
I = r ; err = 1
suku = x
sin = suku
while err > 1e-7
{
ratio = -x^2/((2*I)*(2*I+1))
suku = suku*ratio
err = abs(suku/sin)
sin = sin + suku
I = I+1
}
Dalam sebuah program, ada tiga komponnen, RAM, controller, ALU(Arithmetic Logic Unit). Misalnya dalam RAM ada nilai a=2. Controller memiliki sebuah fungsi a=a+2. Jika program dijalankan ALU akan merubah nilai a pada ram menjadi a+2=4. Alur ini merupakan alur yang sudah umum ada pada sebuah program.
Turunan Numerik, Selasa 17 September 2019:
Turunan numerik ada 3, maju, mundur, dan center. Untuk nilai h yang sama, center adalah turunan numerik paling baik, sementara maju dan mundur dapat dibilang ada dalam tingkat keakuratan yang sama. Hal ini juga bergantung nilai h, karena semakin besar nilai h semakin besar juga truncation error, yaitu kesalahan akibat pemotongan dari deret taylor, jika menggunakan h = 0.2 pada turunan center sementara digunakan h = 0.001 pada turunan maju, akan lebih akurat nilai dari turunan maju. Rumus dibawah merupakan rumus turunan pertama untuk turunan center dan mundur.
Turunan mundur Turunan center
Cara menghitung dengan table, pakai gradien aja, dianggap dia garis lurus (y2-y1)/(x2-x1). Kalo nariknya ke depan dari titik yang dicari, jadi turunan maju, kalo ke belakang jadi turunan mundur. Dari cara ini, dapat dibuktikan nilai dari cara menggunakan table akan sama dengan cara turunan biasa.
Secant Method, Bisect Method, dan Newton Raphson Method, Selasa 24 September 2019:
Secant, bisect, dan Newton-Raphson method, digunakan dalam pencarian pembuat nol dari sebuah fungsi, atau biasa disebut root-finding algorithm.
Secant Method
Secant method menggunakan secant lines untuk mengaproksimasi nilai sebuah fungsi. Metode ini mirip dengan metode Newton-Raphson hanya saja menggunakan finite-difference.
Bisect Method
Merupakan metode pencarian akar-akar untuk fungis yang kontinu, dimana diketahui nilai x pada f(x) bernilai positif dan f(x) bernilai negative
Newton-Raphson Method
Truncation Error, Rounding Error, Persamaan Banyak, Selasa 1 Oktober 2019:
Semua metode numerik memiliki truncation error, baik itu Newton-Raphson, finite element, finite difference dst., dan semua software memiliki truncation error. Untuk memperkecil truncation error, meshing harus dilakukan dengan partisi yang kecil. Apa itu meshing? meshing merupakan pembagian daerah yang dianalisis menjadi partisi-partisi yang sangat kecil, semakin kecil partisi tersebut, semakin akurat hasilnya. Walaupun demikian, hasil yang dihasilkan dari metode numerik tetap diskrit, walaupun terlihat kontinum jika partisinya sangat kecil. Tetapi tidak selalu demikian kasusnya, jika partisi terlalu kecil, maka jumlah iterasi akan semakin banyak, artinya jumlah pengoperasian perhitungan bertambah banyak, dan jumlah rounding akan semakin banyak sehingga rounding error semakin besar. Jadi, untuk menentukan sebesar apa partisinya, ada nilai optimumnya. Untuk mengetahui nilai N (jumlah iterasi) yang paling optimum, nilai iterasi divariasikan dari kecil hingga besar, saat dia sudah tidak berubah banyak maka di titik tersebut lah jumlah iterasinya paling optimum. Begitu juga dengan jumlah mesh perlu divariasikan agar mendapat nilai yang paling optimum.
Pada sebuah penelitian, jika ingin memvalidasi hasil perhitungan numerik, agak kurang logis. Mengapa? karena pada eksperimen error berbeda dengan error pada numerik. Pad numerik, errornya antara lain, rounding error, truncation error, kesalahan asumsi, dan penyederhanaan, sementara pada eksperimen hanya ada error alat ukur. Jadi apa gunanya numerik? Pada sebuah kotak, pada eksperimen mungkin hanya bisa mengukur temperature pada boundary saja, tetapi numerik bisa menghitung hingga bagian dalamnya. Hasil dari metode numerik tidak akan bisa sama dengan eksperimen, tetapi hanya mungkin memiliki trend yang sama. Misalnya, pada eksperimen grafik yang didapat cendrung turun, begitu juga pada numerik, artinya numerik masih bisa dapat kita percayan sebagai alat untuk Analisa. Jika hal ini terpenuhi, maka hasil eksperimen dapat kita Analisa dengan menggunakan metode numerik terutama pada bagian-bagian yang tidak dapat diukur oleh eksperimen.
Multiple equations (?)
PR Pemodelan Matematika dari Kecepatan Maksimal Mobil, dan Pseudocode untuk Penyelesaiannya, Selasa 29 Oktober 2019:
Pada kesempatan kali ini, saya mendapatkan tugas untuk membuat pemodelan sebuah mobil dan mencari kecepatan maksimum yang didapatkan dengan menggunakan metode numerik. Dalam pemodelan ini, diasumsikan hanya gaya gesek udara dan gaya gesek ban yang menjadi penghambat, serta gaya hasi dari motor bakar untuk akselerasi. Efisiensi transmisi diasumsikan 100%. Pemodelan dapat dilihat pada gambar dibawah ini.
Setelah dilakukan pemodelan, didapatkan sebuah ODE atau Ordinary Differential Equation. ODE dapat diselesaikan dengan beberapa cara, salah satunya dengan metode Runge-Kutta. Metode Runge-Kutta merupakan metode untuk melakukan plot grafik respon transien dari suatu system. Metode Runge Kutta mengikuti algoritma dibawah ini dengan pseudocode seperti gambar dibawahnya
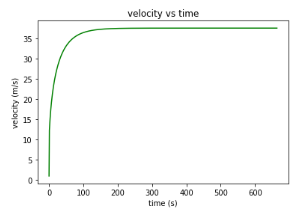
Kemudian saya menulis sebuah code dalam Bahasa Python dengan menggunakan IDE Jupyter Notebook, didapatkan hasil berupa grafik bahwa steady-state dapat dilihat ada pada sekitar detik 100-200 dengan nilai sebesar 35.
File video berikut ini merupakan step-step dari coding tersebut dalam IDE Spyder
Menghitung Drag dengan CFDSOF-NG, Regresi Gaya Drag, dan Perhitungan Transient Response dari Fungsi Kecepatan Maksimum Mobil, Selasa 5 November 2019:
CFDSOF-NG merupakan sebuah aplikasi yang menerapkan metode-metode CFD(Computational Fluid Dynamics) buatan Indonesia. Pada kesempatan kali ini kami menggunakan CFDSOF-NG untuk menghitung besarnya gaya drag yang terjadi pada sebuah model mobil. Gaya yang didapat dari hasil simulasi akan kami plot dan lakukan regresi yang kemudian merubah fungsi drag pada pemodelan matematika kecepatan maksimal mobil.
1) Langkah pertama adalah membuat pemodelan CAD untuk mobil. Model ini dapat kita modelkan sendiri atau dapat kita cari di GrabCAD. Namun, untuk kesempatan kali ini, kami menggunakan model yang telah diberikan oleh asisten dosen.
2) Langkah kedua adalah menyimpan file dalam format .stl dan kemudian dipindahkan ke CFDSOF-NG.
3) Lakukan meshing dengan mesh 2 dimensi saja, dan check mesh apakah sudah benar.
4) Pilih bagian mana dari mesh yang menjadi inlet dan outlet, serta bagian bawah menjadi wall. Sementara itu, untuk bagian kanan dan kiri dijadikan empty karena simulasi hanya dua dimensi
5) Pilih jenis aliran dan properties udara yang diinginkan
6) Setelah semuanya dipilih, lakukan simulasi
7) Setelah simulasi selesai, lihat hasilnya di Paraview.
8) Kalkulasi drag dilakukan pada Paraview dengan mengalikan nilai pressure dengan normal arah x, atau arah yang berlawanan dengan arah gerak mobil.
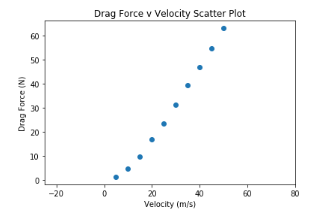
9) Setelah didapatkan titik-titik tersebut, lakukan plot dan lihat trend grafiknya
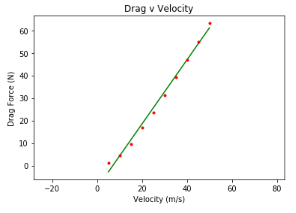
10) Saya mendapatkan trend grafik yang linear sehingga dilakukan regresi linear.
11) Setelah mendapatkan fungsi dari regresi linear, gantilah fungsi drag force pada pemodelan dengan fungsi hasil regresi, dan lakukan simulasi kembali
Setelah mendapatkan hasil tersebut, saya mencoba melakukan komputasi pada program Python yang saya buat sendiri. Coding dalam Bahasa Python dapat dilihat pada gambar dibawah ini.
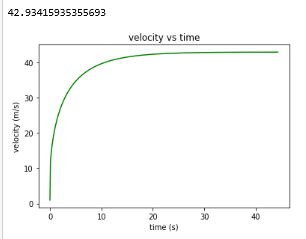
Dari hasil coding tersebut didapatkan beberapa grafik. Grafik pertama merupakan scatter plot untuk melihat trend dari titik-titik yang didapatkan sesuai dengan langkah 9. Kemudian karena trend-nya linear kami menggunakan regresi linear sehingga didapatkan sebuah drag force sebagai fungsi kecepatan yang linear. Hasil tersebut dimasukkan ke dalam pemodelan matematika. Kemudian dilakukan plot grafik dengan metode Runge-Kutta dan dipatkan grafik respon transien. Didapatkan kecepatan maksimal sebesar 42m/s.
Melakukan Optimasi Lift-to-Drag Ratio dengan Simulasi CFDSOF-NG, Selasa 19 November 2019:
Optimasi merupakan proses mencari nilai maksimum atau minimum dari sebuah kurva yang diberikan. Cara termudah dari optimasi tentu dengan menurunkan satu kali lalu hasil turunan tersebut disamadengankan dengan nol. Tetapi tidak selalu semudah itu, seringkali optimasi dilakukan dengan banyak Batasan, hal inilah yang kita sebut constrained optimization. Pada kesempatan kali ini, saya berkesempatan melakukan optimasi lift-to-drag ratio pada sebuah airfoil.
Lift-to-drag ratio merupakan sebuah rasio antara lift force dan drag force. Parameter ini menjadi penting karena kita tentu ingin mencari flight condition terbaik untuk sebuah pesawat dimana dibutuhkan thrust seminimal mungkin untuk mendapatkan lift yang besar dan drag sekecil mungkin, yang bisa kita dapatkan pada nilai lift-to-drag ratio paling besar. Langkah-langkah dalam tugas ini sebagai berikut.
1) Melakukan pemodelan dengan CAD (Inventor) atau download pada GrabCAD dan di-export dalam format .stl
2) Di-import ke CFDSOF-NG dan lakukan simulasi. Kali ini tidak hanya mencari drag force tetapi juga lift force.
3) Lakukan plot lift force, plot drag force, dan plot lift-to-drag ratio
4) Untuk masing-masing scatter plot perhatikan trendnya, apakah linear atau polynomial
5) Lakukan regresi sesuai dengan hasil scatter plot
6) Setelah dilakukan regresi, lakukan optimasi
Pada kesempatan kali ini didapatkan trend grafik paling mendekati fungsi polynomial pangkat enam sehingga dilakukan regresi pangkat enam. Saya mencoba melakukannya dengan tiga metode, 1) Multiple Linear Regression dengan nilai x1 = x^1, x2 = x^2, dst. 2) Polynomial Regression untuk polynomial pangkat enam, 3)Excel. Karena untuk metode pertama dan kedua penyelesaiannya dengan matriks dan harus dilakukan eliminasi Gauss-Jordan, maka saya melakukan coding dalam Bahasa Python untuk melakukan hal tersebut.