Difference between revisions of "Report Tugas Kelompok 4 : Metode Numerik 2019"
(→Optimasi) |
(→Optimasi) |
||
| Line 65: | Line 65: | ||
import numpy as np | import numpy as np | ||
| − | from scipy.optimize import minimize | + | from scipy.optimize import minimize |
| − | |||
| − | |||
| − | |||
def calc_drag(x):#drag | def calc_drag(x):#drag | ||
Revision as of 23:21, 8 December 2019
Anggota Kelompok:
- Fikridiya Bagusrana (1706036154)
- Rifky Ramadhan Prakoso (1706036330)
- Mochamad Farhan Zidny (1706986391)
- Andika Ridwan Pratama (1706986302)
Contents
[hide]Tugas 1
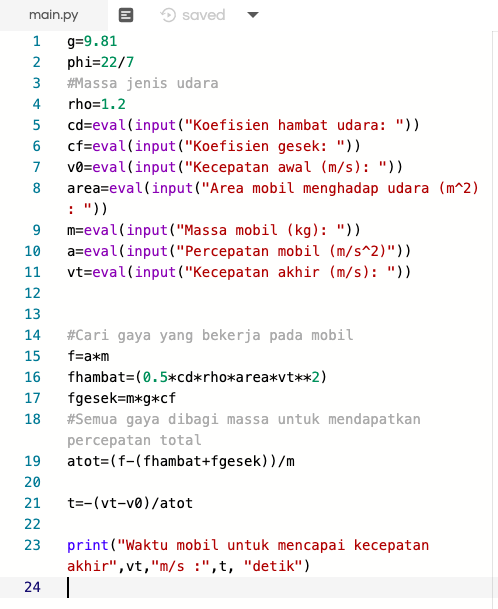
Berikut adalah governing equation pada mobil yang memiliki percepatan, gesekan, dan hambatan dengan udara.
Sebuah mobil memiliki 3 gaya yang bekerja padanya yaitu:
- F = m*a
- F gesek = m*g*cf
- F hambat = 0.5*cd*rho*area*vt^2
Dengan membagi ketiga gaya tersebut dengan massa didapatkan percepatan total
v'(t)= (F - (F gesek + F hambat))/m
Kemudian apabila disubsitusikan ke turunan dari kecepatan terhadap waktu
v'(t)= v(t)/t
dapat dicari waktu dengan cara membagi kecepatan dengan percepatan total, dimana percepatan total adalah turunan dari kecepatan terhadap waktu
t= v(t) / ((F - (F gesek + F hambat))/m)
Tugas 2
Tugas 3
Case Description
- Airfoil memiliki karakteristik aerodinamis dan merupakan benda yang sering digunakan contohnya pada pesawat
- Thrust pada pesawat berpengaruh pada effisiensi aerodinamis, maka dari itu dibutuhkan Cl/Cd yang kecil. Cl dan Cd tergantung pada angle of attack dari airfoil.
- Airfoil yang digunakan kali ini adalah airfoil NACA 0012
- Fluida udara yang melewat air foil steady flow dan incompressible, simulasi CFD dalam kondisi adiabatic
Kemudian Airfoil yang digunakan dilakukan variasi pada 6 angle of attack yang berbeda berupa (degrees):
- 0
- 2
- 4
- 6
- 8
- 10
Simulasi CFD SOF
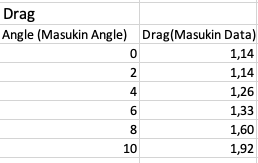
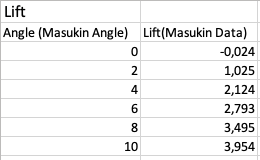
Kemudian dilakukan simulasi airfoil dan didapatkan data sebagai berikut,
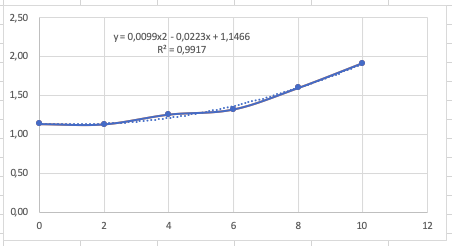
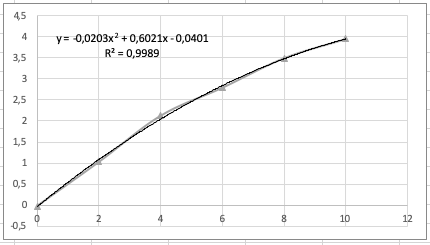
Kemudian data tersebut direpresentasikan dalam bentuk grafik pada excel,
Optimasi
Didapatkan rumus drag berupa y = 0,0005x3 + 0,0031x2 + 0,0027x + 1,1357 dan juga rumus lift berupa y = -0,0203x2 + 0,6021x - 0,0401. Dari kedua rumus tersebut kemudian dimasukkan dalam program python dibawah ini:
import numpy as np from scipy.optimize import minimize
def calc_drag(x):#drag x1 = x[0] drag = 0.0099*x1**2-0.0223*x1**1+1.1466 return drag
def calc_lift(x): #lift x1 = x[0] lift = -0.0203*x1**2+0.6021*x1**1-0.0401 return lift
def objective(x): #volume yang diminimalkan return calc_drag(x)
def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag return 90 - calc_drag(x) def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift return 90 - calc_lift(x)
con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)
x1_guess = 50
x0 = np.array([x1_guess])
sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})
xopt = sol.x forceopt = -sol.fun
dragopt = calc_drag(xopt) # drag optimal liftopt = calc_lift(xopt) # lift optimal
print ('sudut optimal = '+str(-xopt[0]))
print ('total force optimal = '+str(forceopt))
print ('drag force optimal = '+str(-dragopt))
print ('lift force optimal = '+str(liftopt))
# In[10]:
import numpy as np from scipy.optimize import minimize
def calc_drag(x):#drag x1 = x[0] drag = 0.0099*x1**2-0.0223*x1**1+1.1466 return drag
def calc_lift(x): #lift x1 = x[0] lift = -0.0203*x1**2+0.6021*x1**1-0.0401 return lift
def objective(x): #volume yang diminimalkan return calc_lift(x)
def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag return 90 - calc_drag(x) def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift return 90 - calc_lift(x)
con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)
x1_guess = 50
x0 = np.array([x1_guess])
sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})
xopt = sol.x forceopt = -sol.fun
dragopt = calc_drag(xopt) # drag optimal liftopt = calc_lift(xopt) # lift optimal
print ('sudut optimal = '+str(xopt[0]))
print ('total force optimal = '+str(-forceopt))
print ('drag force optimal = '+str(dragopt))
print ('lift force optimal = '+str(liftopt))
Kemudian setelah program dijalan didapatkan hasil sebagai berikut:
Optimization terminated successfully. (Exit mode 0)
Current function value: 1.1340421717179265
Iterations: 5
Function evaluations: 15
Gradient evaluations: 5
sudut optimal = -1.1262713580043062
total force optimal = -1.1340421717179265
drag force optimal = -1.1340421717179265
lift force optimal = 0.6122776950656171
Optimization terminated successfully. (Exit mode 0)
Current function value: -128.89494468045336
Iterations: 7
Function evaluations: 24
Gradient evaluations: 7
sudut optimal = 95.86991386912578
total force optimal = -128.89494468045336
drag force optimal = 90.00000073492711
lift force optimal = -128.89494468045336