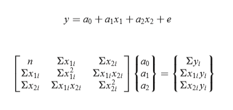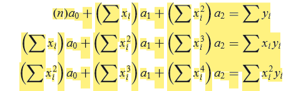Difference between revisions of "Report Tugas Kelompok 10 : Metode Numerik 2019"
Puntasingga (talk | contribs) |
Puntasingga (talk | contribs) |
||
| Line 65: | Line 65: | ||
| − | [[File:Screenshot (2).png| | + | [[File:Screenshot (2).png|600px]] |
| − | [[File:Screenshot (103).png| | + | [[File:Screenshot (103).png|600px]] |
| − | [[File:Screenshot (4).png| | + | [[File:Screenshot (4).png|600px]] |
| Line 77: | Line 77: | ||
[[File:12345.PNG]] | [[File:12345.PNG]] | ||
| − | [[File:Screenshot (6).png| | + | [[File:Screenshot (6).png|600px]] |
| − | [[File:Screenshot (7).png| | + | [[File:Screenshot (7).png|600px]] |
| − | [[File:Screenshot (80).png| | + | [[File:Screenshot (80).png|600px]] |
| − | [[File:Screenshot (9).png| | + | [[File:Screenshot (9).png|600px]] |
| Line 90: | Line 90: | ||
[[File:1234.PNG]] | [[File:1234.PNG]] | ||
| − | [[File:Screenshot (11).png| | + | [[File:Screenshot (11).png|600px]] |
| − | [[File:Screenshot (12).png| | + | [[File:Screenshot (12).png|600px]] |
| Line 97: | Line 97: | ||
Lalu didapatkan regresi linearnya sebagai berikut : | Lalu didapatkan regresi linearnya sebagai berikut : | ||
| − | [[File:Screenshot (131).png| | + | [[File:Screenshot (131).png|600px]] |
| + | |||
| + | |||
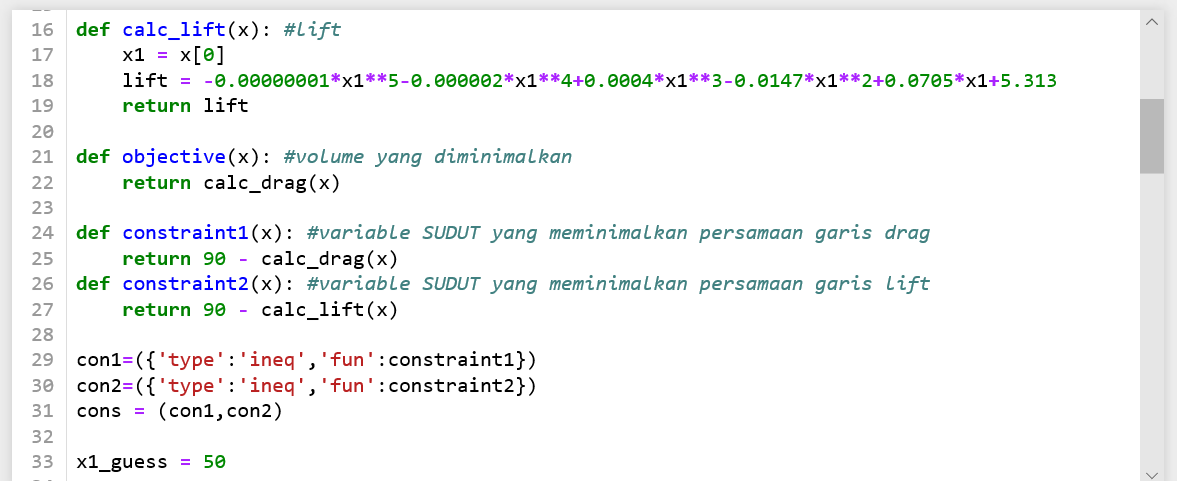
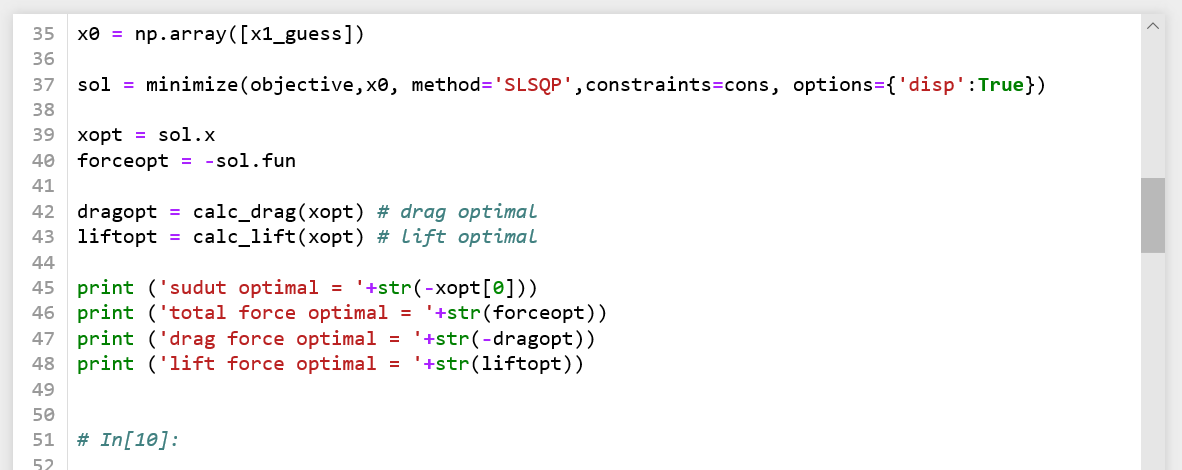
| + | Setelah itu dilakukan coding didalam phyton, ada 2 metode yang kami lakukan dalam optimasi kali ini, yaitu SLSQP dan Gradient Method | ||
| + | |||
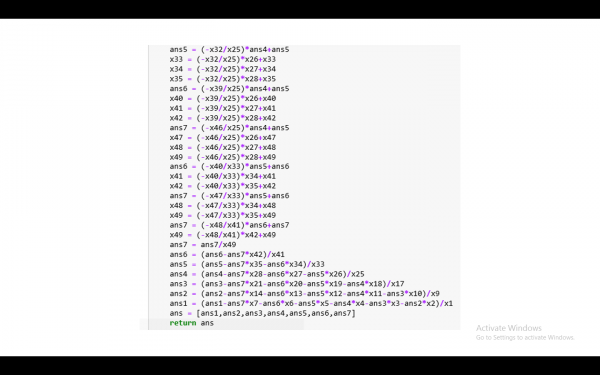
| + | '''SLSQP''' | ||
| + | |||
| + | [[File:Picture11111.png]] | ||
| + | [[File:Picture2222.png]] | ||
| + | [[File:Picture3333.png]] | ||
| + | |||
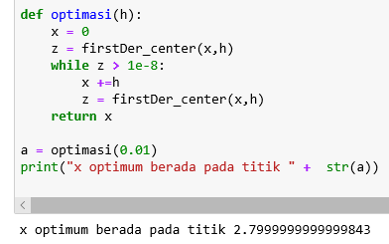
| + | '''Gradient method''' | ||
| + | |||
| + | Pada gradient method, Digunakan penurunan secara metode numerik. pada metode ini, ,menggunakan fungsi dari excel karena paling mendekati bentuk hasil simulasi. Pada metode ini juga, dilakukan while loop hingga gradien sama dengan nol. | ||
| + | |||
| + | [[File:Picture4444.png]] | ||
| + | [[File:Picture5555.png]] | ||
Revision as of 11:59, 3 December 2019
Anggota kelompok:
- Bintang Farhan Muhammad (1706986334)
- Punta Singga Parasdya (1706986473)
- Muhammad Mizan (1806149192)
- Muhammad Abi Rizky (1706036311)
Tugas Pertama, Pemodelan Matematika Mobil, dan Kecepatan Maksimal dengan Metode Runge-Kutta
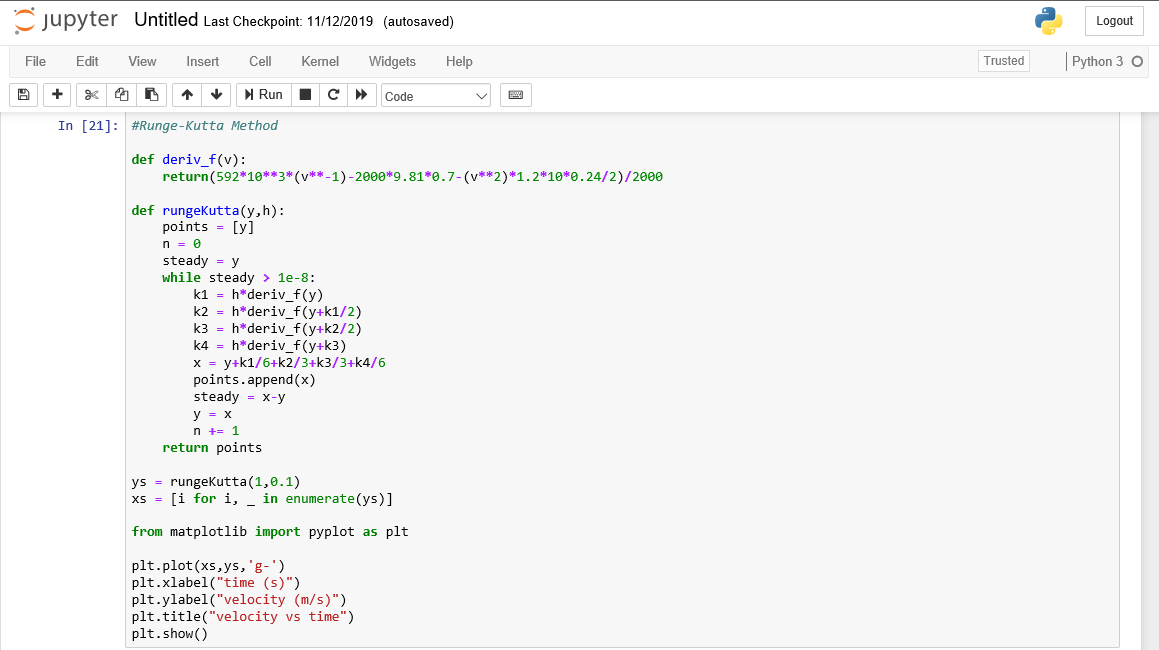
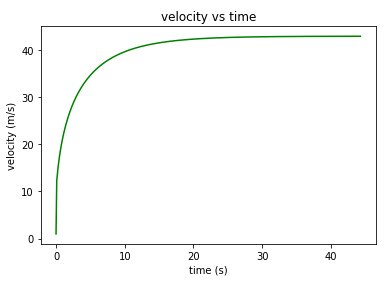
Pada tugas ini, kami melakukan pemodelan matematika pada mobil untuk menghitung kecepatan maksimal mobil. Pemodelan dilakukan dengan membuat FBD pada mobil, dengan hanya memperhitungkan drag force dan gaya gesek dengan jalan. Diasumsikan mechanical loss pada transmisi tidak ada, begitu juga dengan loss lainnya sehingga daya baterai mobil ditransmisikan 100% ke roda. Kami memilih mobil Tesla sebagai bahan dalam pemodelan ini, dengan spesifikasi mobil sebagai berikut:
Dengan spesifikasi tersebut, didapatkan hasil pemodelan seperti ini.
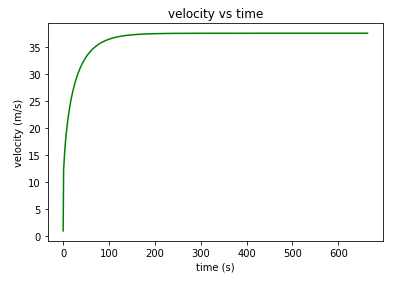
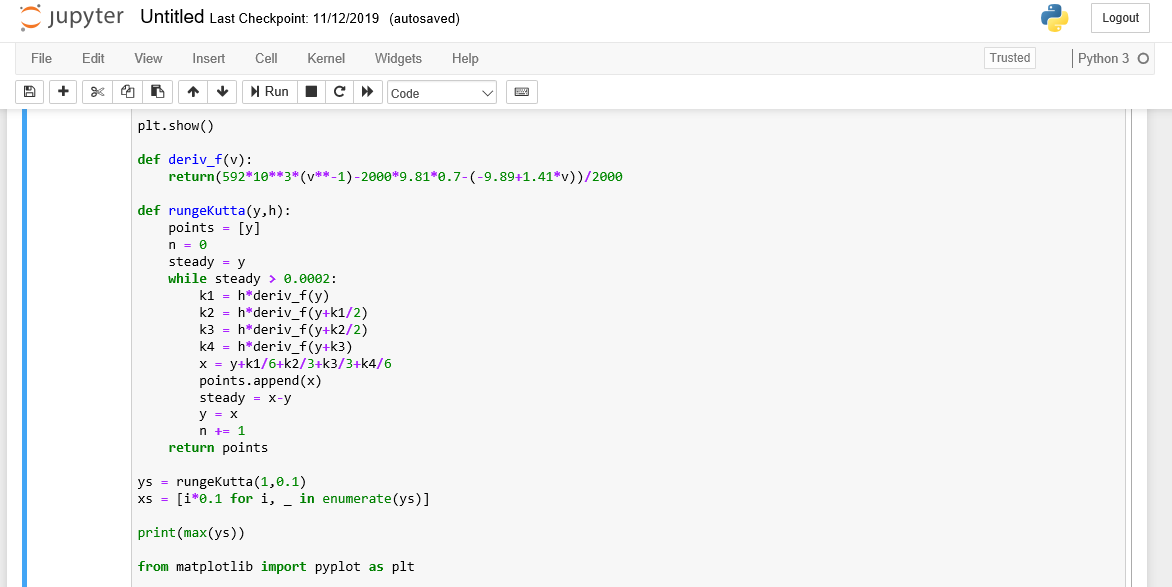
Dari hasil pemodelan tersebut kami lakukan perhitungan dengan metode numerik untuk mendapatkan grafik respon transien agar diketahui kecepatan maksimumnya. Code yang kami tulis dapat dilihat pada gambar dibawah ini.
Tugas Kedua, Curve Fitting Drag Force Mobil
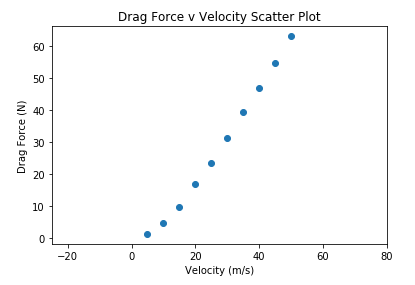
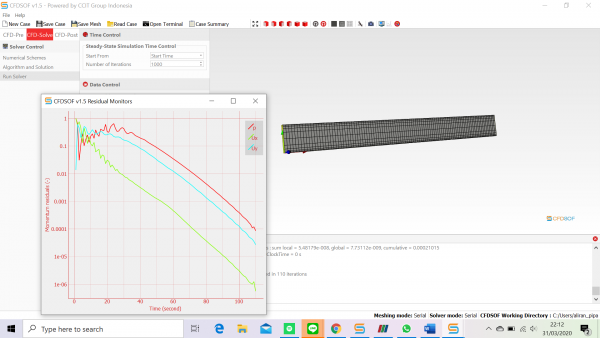
Pada tugas ini kami mensimulasikan drag force pada mobil dengan menggunakan CFDSOF-NG. Model mobil yang digunakan dapat dilihat seperti pada gambar dibawah ini. Kami melakukan simulasi dengan rentang kecepatan 0-50m/s dengan interval 5m/s dan didapatkan data sebagai berikut:
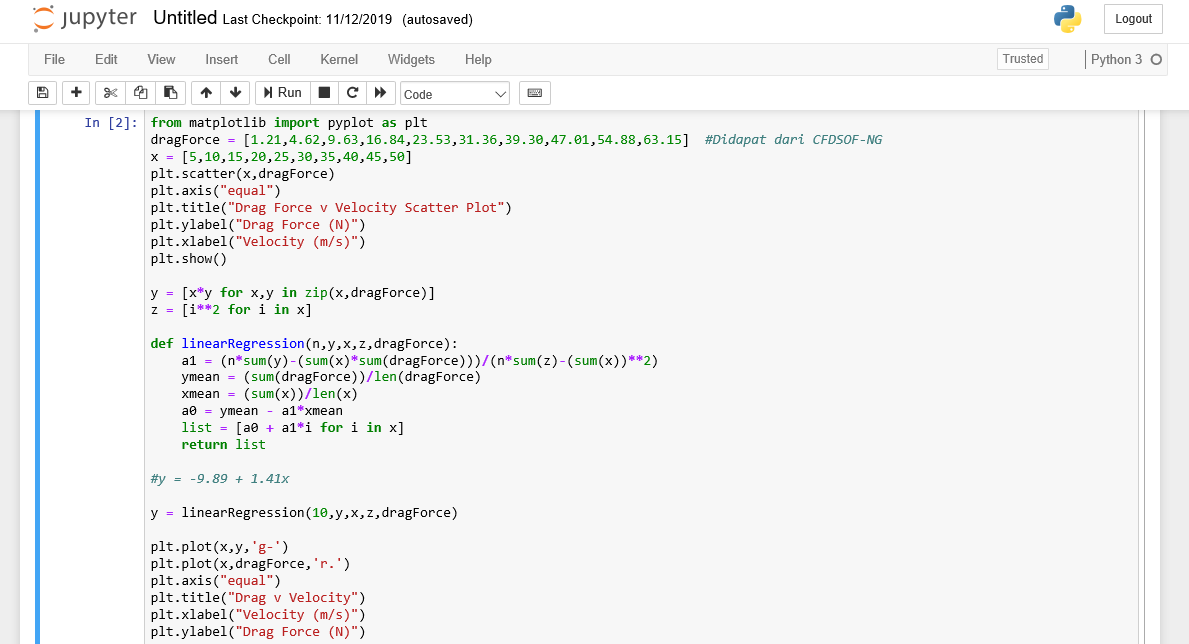
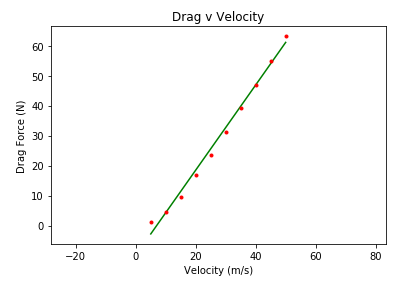
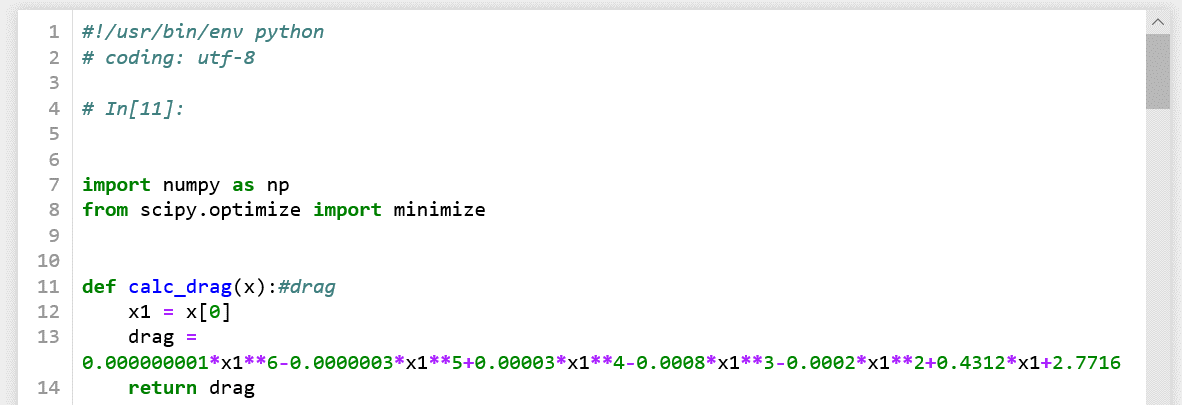
Setelah didapatkan data tersebut, kami melakukan coding pada program python, dan dilakukan scatter plot. Dapat dilihat bahwa trend grafik cendrung linear sehingga kami memutuskan untuk menggunakan regresi linear. Code Python dapat dilihat pada gambar dibawah ini.
Tugas Ketiga, Optimasi Airfoil Menggunakan Python dengan Simulasi CFDSOF-NG
Pada tugas ini kami ditugaskan untuk mencari sudut optimal airfoil dengan menggunakan CFDSOF-NG.
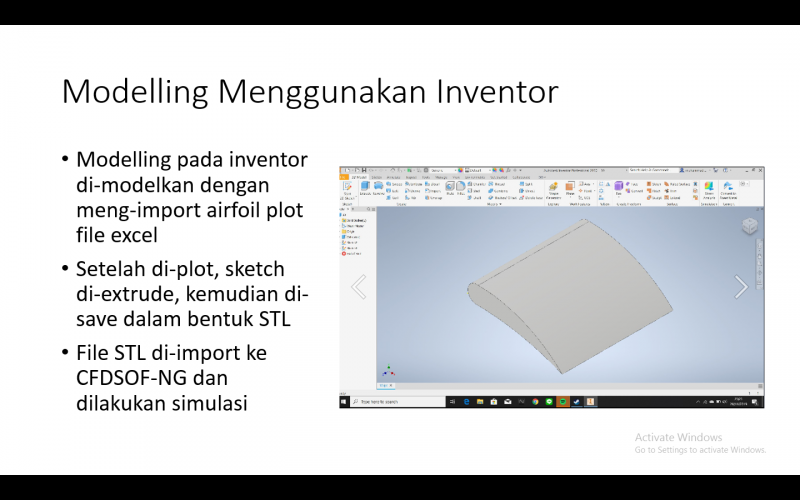
hal pertama yang dilakukan adalah modelling menggunakan inventor.
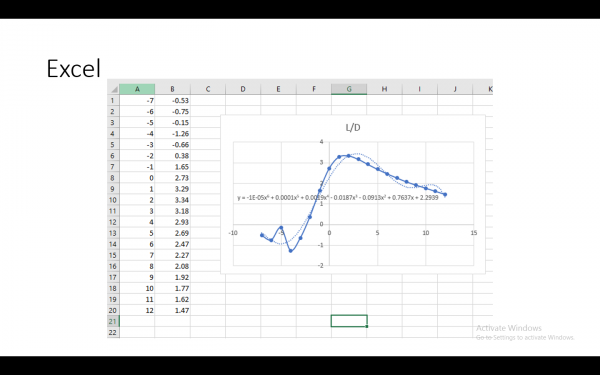
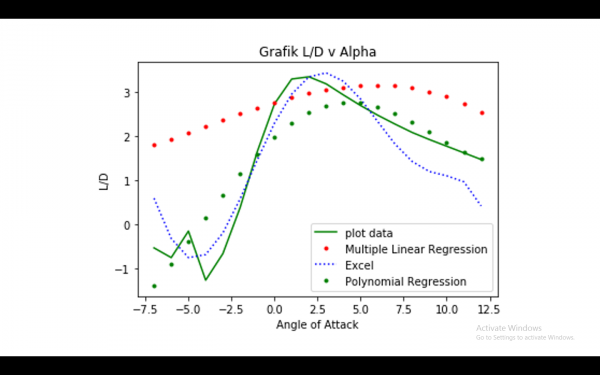
Selanjutnya kami mencari persamaan dengan regresi linear. Grafik naik turun mendekati persamaan polynomial pangkat enam.
Dilakukan regresi polynomial dengan tiga cara :
Excel
Polynomial regression
Multiple linear regression
Dengan excel
Dengan multiple linear regression
Dengan Polynomial Regression
Lalu didapatkan regresi linearnya sebagai berikut :
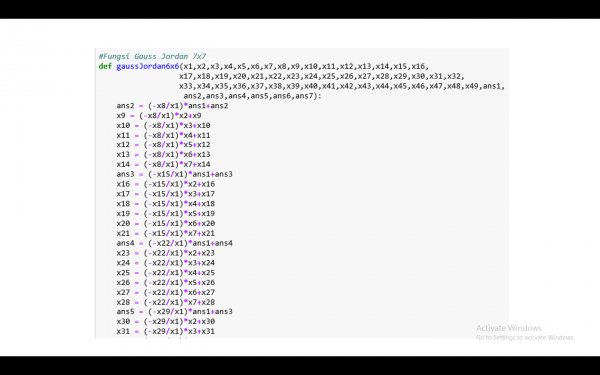
Setelah itu dilakukan coding didalam phyton, ada 2 metode yang kami lakukan dalam optimasi kali ini, yaitu SLSQP dan Gradient Method
SLSQP
Gradient method
Pada gradient method, Digunakan penurunan secara metode numerik. pada metode ini, ,menggunakan fungsi dari excel karena paling mendekati bentuk hasil simulasi. Pada metode ini juga, dilakukan while loop hingga gradien sama dengan nol.