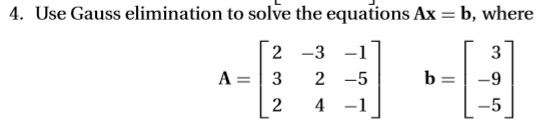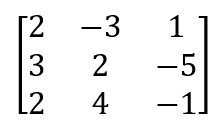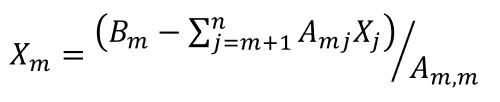Difference between revisions of "Kelompok 7"
(→Analisis Gaya Drag Mobil pada CFDSOF-NG) |
|||
| Line 161: | Line 161: | ||
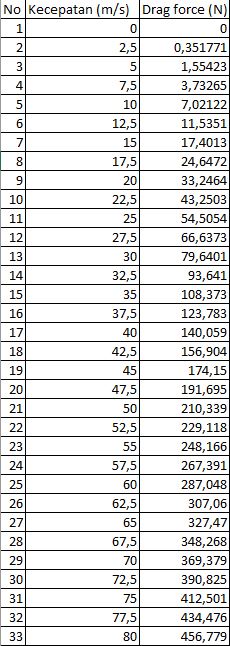
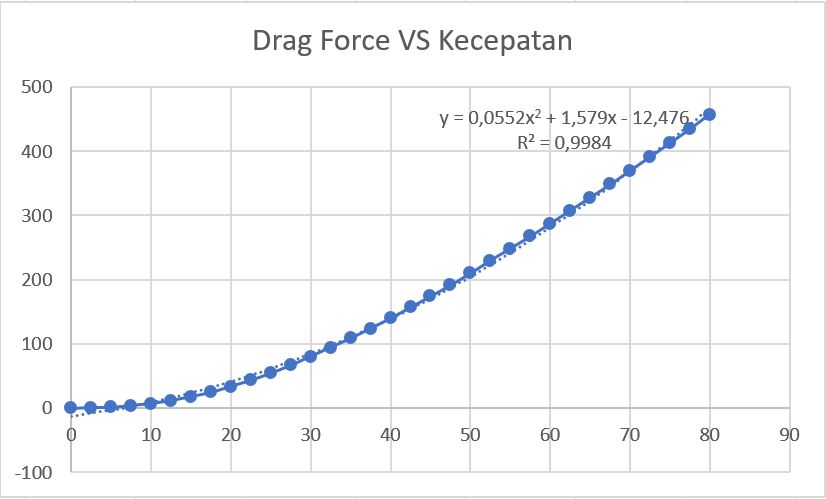
== Analisis Gaya Drag Mobil pada CFDSOF-NG == | == Analisis Gaya Drag Mobil pada CFDSOF-NG == | ||
| + | |||
| + | [[File:Hasil Iterasi Kelompok7.JPG]] | ||
| + | |||
| + | [[File:Drag Force vs kec. Kelompok7.JPG]] | ||
Revision as of 14:40, 12 November 2019
Contents
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Perkenalkan, kami dari kelompok 7 dengan anggota kelompok sebagai berikut:
1. Rizki Aldila Umas
2. Hallyena Risfenti
3. Dimaz Adhitya
Metode Eliminasi Gauss
Dalam pembuatan tugas mengenai eliminasi gauss ini, kelompok kami memilih untuk langsung mengambil contoh dari buku Jaan Kiusalaas, yaitu:
Pengerjaan Matematis
Dalam pengerjaan Eliminasi Gauss, setidaknya ada 2 langkah yang harus dilalui. Kedua langkah tersebut adalah
1. Eliminasi Gauss
Dimulai dengan gauss yang ada di contoh soal tersebut
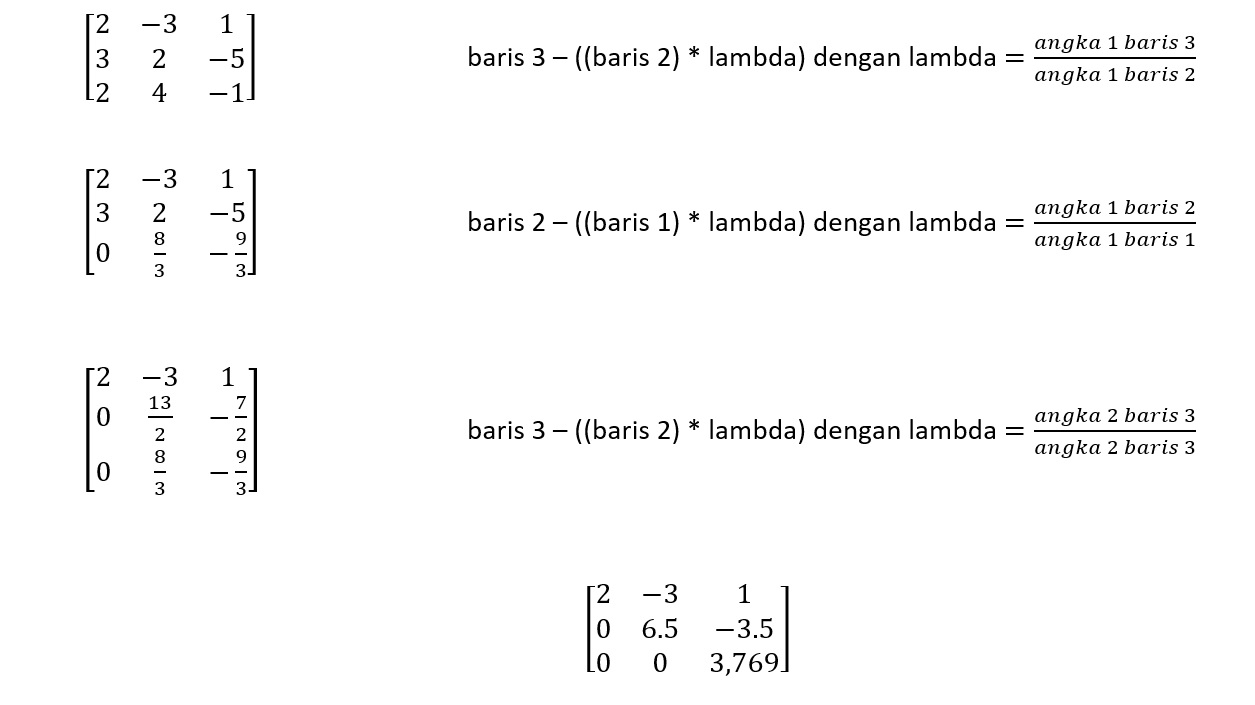
Untuk membuat segitiga atas pada matriks ini maka diperlukan operasi sebagai berikut:
Sehingga dapat digeneralisasi fungsi untuk lambda dan bentuk iterasinya sehingga menghasilkan segitiga atas. Pada matriks B juga dilakukan operasi yang sama dengan matriks A (harus diperlakukan sama dengan matriks A)
2. Back Substitution
Pada back substitution ini, secara matematis maka dimasukkan satu per satu mulai dari X yang paling rendah dan ada di bawah, dan kemudian naik. Hal ini dapat dirumuskan menjadi suatu fungsi berupa:
Pengerjaan Menggunakan Phyton
Dalam pengerjaan Eliminasi Gauss dengan menggunakan phyton setidaknya ada 3 langkah yang harus diselesaikan terlebih dahulu, tambahan 1 langkah tersebut jika dibandingkan dengan pengerjaan menggunakan matematis adalah pendefinisian matriks. Sehingga secara umum langkah pengerjaan Eliminasi Gauss dengan menggunakan phyton adalah sebagai berikut:
1. Pendefinisian Matriks
Pendefinisian tersebut dibantu dengan menggunakan fungsi array dari numpy dengan cara import numpy.
2. Eliminasi Gauss
3. Back Substitution
Berikut video penjelasannya:
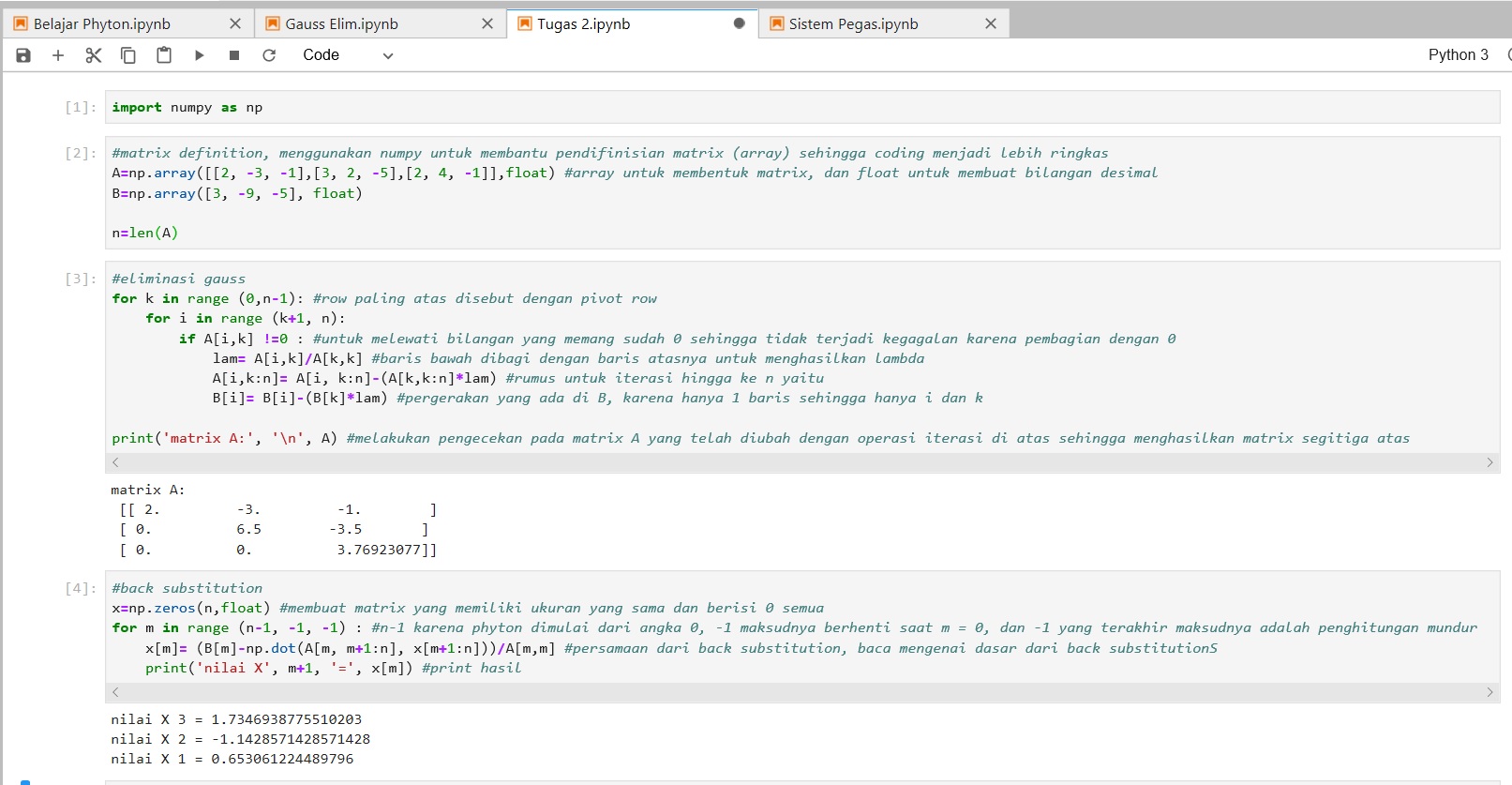
Berikut ini beberapa screenshoot dari kode phyton yang telah kami susun:
Aplikasi Metode Numerik
Berikut merupakan video untuk menyelesaikan soal fondasi menggunakan Gauss Elimination
Metode Runge Kutta Orde 4
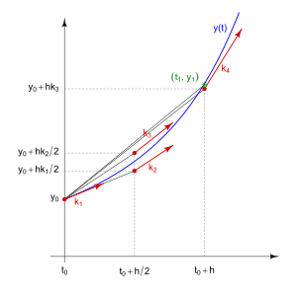
Runge Kutta merupakan metode untuk pendekatan suatu nilai persamaan yaitu dengan melakukan segmentasi-segmentasi dengan suatu garis-garis lurus dari suatu titik ke titik berikutnya mengikuti segmentasi yang dibuat. Runge Kutta terdiri dari beberapa orde, diantanya adalah orde 2, orde 3, dan orde 4. Perbedaan dari beberapa orde tersebut adalah: Runge Kutta Orde 4 lebih akurat dari Orde 3, sedangkan Runge Kutta Orde 3 lebih akurat dari Orde 2.
Dalam tugas kali ini kami akan membuat Runge Kutta Orde 4 untuk menyelesaikan suatu permasalahan pegas. Secara umum persamaan Runge Kutta Orde 4 adalah sebagai berikut:
𝑦_(𝑖+1)=𝑦_𝑖+1/6 (𝑘_1+2𝑘_2+2𝑘_3+𝑘_4 )ℎ
Dengan :
𝑘_1=𝑓(𝑥_𝑖,𝑦_𝑖 )
𝑘_2=𝑓(𝑥_𝑖+1/2 ℎ,𝑦_𝑖+1/2 𝑘_1 ℎ)
𝑘_3=𝑓(𝑥_𝑖+1/2 ℎ,𝑦_𝑖+1/2 𝑘_2 ℎ)
𝑘_4=𝑓(𝑥_𝑖+1/2 ℎ,𝑦_𝑖+1/2 𝑘_3 ℎ)
Selanjutnya akan langsung ke pendefinisian soal yaitu sebagai berikut:
Penyelesaian masalah ini adalah dengan algoritma sebagai berikut:
1. Awalnya fungsi yang ada pada soal tersebut adalah suatu fungsi percepatan sehingga harus diubah terlebih dahulu menjadi suatu fungsi turunan dari fungsi jarak yaitu fungsi kecepatan. Perubahan itu adalah dengan menggunakan integral satu kali terhadap waktu sehingga mendapatkan fungsi kecepatan. Setelah itu didefinisikan suatu persamaan pada tiap keadaannya yaitu pada keadaan t kurang dari 2 dan t lebih dari sama dengan 2.
2. Fungsi kecepatan merupakan suatu fungsi jarak terhadap waktu yang nantinya akan dipakai untuk mencari nilai jarak terhadap fungsi waktu yang diminta pada soal. Hal ini dengan cara menentukan atau mendefinisikan nilai t = 0 yaitu y = 0, dan karena metode ini membutuhkan suatu step size yang disebut increment maka kami memutuskan untuk menggunakan increment (h) dengan kenaikan 0,01.
3. Runge kutta dikerjakan seperti pada persamaan yang telah disampaikan di awal.
𝑦_(𝑖+1)=𝑦_𝑖+1/6 (𝑘_1+2𝑘_2+2𝑘_3+𝑘_4 )ℎ
Dengan :
𝑘_1=𝑓(𝑥_𝑖,𝑦_𝑖 )
𝑘_2=𝑓(𝑥_𝑖+1/2 ℎ,𝑦_𝑖+1/2 𝑘_1 ℎ)
𝑘_3=𝑓(𝑥_𝑖+1/2 ℎ,𝑦_𝑖+1/2 𝑘_2 ℎ)
𝑘_4=𝑓(𝑥_𝑖+1/2 ℎ,𝑦_𝑖+1/2 𝑘_3 ℎ)
4. Hasil dari persamaan tersebut lalu di plot antara t atau waktu yang diberikan dan hasil y atau osilasi yang dilakukan
Alur untuk menyelesaikan masalah berikut adalah dengan flowchart seperti berikut ini:
Dan diselesaikan dengan persamaan phyton berikut ini:
# Pendefinisian nilai awal atau initial value dan increment yang akan digunakan (h). Kita menggunakan h = 0.01.
x0 = 0
y = 0
h = 0.01
x = float(input("Masukkan nilai t: "))
if 0 <= x < 2:
def dydx(x, y):
return (2*x**2 - 30*x*y) #nilai fungsi sudah diintegralkan sekali, dan dimasukkan nilai K dan m nya sehingga membentuk fungsi tersebut
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h) #untuk mengetahui jumlah iterasi yang akan dilakukan maka panjangnya harus dibagi dengan increment yang telah ditentukan (h=0,01)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
elif x >= 2: # Ketika x >= 2, sesuai dengan soal maka nilai P(t) konstan pada 20N
def dydx(x, y):
return (8 - 30*x*y) #hasil dari pengintegralan dan memasukkan nilai P(t) konstan pada 20N
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
else:#untuk nilai lainnya yaitu nilai t saat negatif
print("Mohon masukkan nilai t positif.")
Dalam penyelesaian ini kami belum mampu membuat kode untuk plot, nantinya akan kami kembangkan lagi sehingga dapat menjawab pertanyaan yang ada