Difference between revisions of "Hallyena Risfenti"
| Line 332: | Line 332: | ||
[[File:SP Alin.png]] | [[File:SP Alin.png]] | ||
| + | |||
| + | Berikut adalah persamaan sistem yang sesuai dengan gambar diatas: | ||
| + | F = m*a (sigma Gaya) | ||
| + | 3t - cv = m*a | ||
| + | a = (3t-cv)/m | ||
| + | dv/dt = (3t-cv)/m | ||
| + | |||
| + | Dan berikut penyekesaiannya menggunakan bahasa pemrograman Python: | ||
| + | |||
| + | def DiferensialV(t, v): #DiferensialV merupakan fungsi turunan V terhadap t | ||
| + | return ((3*t - c*v)/m) | ||
| + | m=eval(input("Massa objek (kg) : ")) | ||
| + | c=eval(input("Damping coefficient (Ns/m) : ")) | ||
| + | t0 = 0 #t awal | ||
| + | v0 = 0 #v awal | ||
| + | t = 10 #kecepatan sistem yang dibutuhkan setelah mencapai waktu 10 detik | ||
| + | h = 0.1 #delta yang digunakan | ||
| + | |||
| + | nilai = (int)((t - t0)/h) #menghitung jumlah increment | ||
| + | for i in range(1, nilai + 1): | ||
| + | k1 = h * DiferensialV(t0, v0) #runge kutta | ||
| + | k2 = h * DiferensialV(t0 + 0.5 * h, v0 + 0.5 * k1) | ||
| + | k3 = h * DiferensialV(t0 + 0.5 * h, v0 + 0.5 * k2) | ||
| + | k4 = h * DiferensialV(t0 + h, v0 + k3) | ||
| + | |||
| + | v0 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #sigma nilai k1,k2,k3,k4 ke y' yang baru dan dibagi | ||
| + | t0 = t0 + h | ||
| + | print("Kecepatan sistem pegas: ",v0, "m/s") | ||
Revision as of 13:40, 6 November 2019
بسم الله الرحمن الرحيم
Hello There!
Nama : Hallyena Risfenti (Alin)
NPM : 1706986372
Mahasiswi Teknik Mesin 2017
Contents
Pertemuan Pertama
Hari, Tanggal : Rabu, 4 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pada pertemuan pertama, Bapak Dr. Ahmad Indra atau kerap dipanggil Pak DAI mengajarkan hal utama yang paling mendasar tetapi seringkali dilupakan yaitu berdoa sebelum belajar.
Kemudian para mahasiswa diperkenalkan dengan website air.eng.ui.ac.id. Di mana, website tersebut digunakan untuk meng-upload tugas yang akan diberikan setiap minggunya. Kami kemudian membuat nama pada page yang sudah disediakan dan menulis entry pertama kami yaitu mengenai “mengapa kita harus belajar kalkulus sedangkan kita adalah mahasiswa teknik bukan mahasiswa mipa?” menurut saya sebagai mahasiswi semester 5 mata kuliah yang sedang ditempuh banyak menggunakan persamaan dan juga permodelan matematika yang banyak didapat ketika saya sedang mempelajari kalkulus 1 dan kalkulus 2 pada semester 1 dan semester 2.
Metnum atau metoda numerik merupakan bagian dari ilmu matematika. Numerik itu dapat digunakan sebagai pemecah masalah atau solver bagi mereka yang sudah memiliki ide namun saja perhitungan akan sangat banyak. Pada mata kuliah ini, bahasa pemrograman yang akan digunakan merupakan Python
Pada akhir kelas, kami diberikan sebuah object:
T = T(x) = (X2-1)/(X-1)
jika diselesaikan dengan metoda perhitungan biasa, maka akan didapatkan angka 2. Sedangkan jika menggunakan bantuan computer cara-cara yang dapat digunakan antara lain: algoritma, flowchart, dan program.
Saya menggunakan modul sympy yang saya download atau unduh dari terminal yang sudah ada di laptop saya. Modul sympy ini merupakan python library untuk symbolic mathematics. Sympy memudahkan user untuk menyelesaikan permasalahan matematika dengan metoda yang simple.
Berikut adalah logaritma yang saya buat menggunakan Idle:

Kemudian saya run menggunakan Python Launcher dan mendapatkan hasil 2.
Pertemuan Kedua
Hari, Tanggal : Rabu, 11 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pada kelas ini, Pak Dai menjelaskan mengenai bahasa pemrograman python. Python adalah high level language dan hubungannya dengan numerik serta komputer sangat kuat. Menurut dari sumber yang saya baca yaitu buku Jaan Kiusalaas, Numerical Methods in Engineering and Python 3,Python merupakan object-oriented language yang mulai dikembangkan dari akhir 1980s.
Keuntungan dari Python sendiri antara lain: 1. Merupakan software yang bersifat open-source, 2. Tersedia untuk major operating system, 3. Lebih mudah untuk dipelajari, 4. Mudah untuk diinstall
Artificial Intelligence atau bisa dikenal dengan AI merupakan rekayasa yang dibuat oleh manusia untuk membantu manusia tersebut. Manusia itu sendiri membutuhkan bantuan dikarenakan kemampuan manusia untuk menghafal sesuatu itu terbatas. Sebagai contoh, jika seorang manusia itu bermain catur melawan komputer, komputer sudah menyimpan database-database untuk mengingat gerakan-gerakan. Hanya saja perbedaan terbesar antara Artificial Intelligence dan manusia adalah manusia memiliki hati.
Menurut Pak Dai, Industry 5.0 adalah pancasila karena seharusnya teknologi itu harus membantu manusia sehingga teknologi tidak boleh melemahkan manusia dan mengakibatkan manusia menjadi bodoh. Selain itu manusia tidak boleh sepenuhnya dikendalikan oleh teknologi tetap harus kita yang mengendalikan teknologi.
Dikarenakan komputer merupakan partner yang kita sering gunakan, maka kita harus mengenal komputer. Secara fisik komputer itu hanya mengenal tombol on atau off. Huruf, kata, maupun kalimat yang kita ketik pada keyboard komputer kita masing-masing dipresentasikan komputer dalam bentuk coding. Pada komputer dikenal pula istilah 32 bit dan 64 bit.
Seperti dalam otak kita, kita manusia mampu menyimpan data-data dalam binary digit. Jika 64 bit maka komputer memiliki kemampuan yang lebih akurat dan cepat. Kemudian informasi tambahan yang saya dapatkan, pada 32 bit processor kemampuan pengolahan untuk berinteraksi dengan RAM terbatas sampai dengan 4GB, sedangkan pada 64 bit processor kemampuan pengolahan untuk berinteraksi dengan RAM bisa lebih dari 4GB.
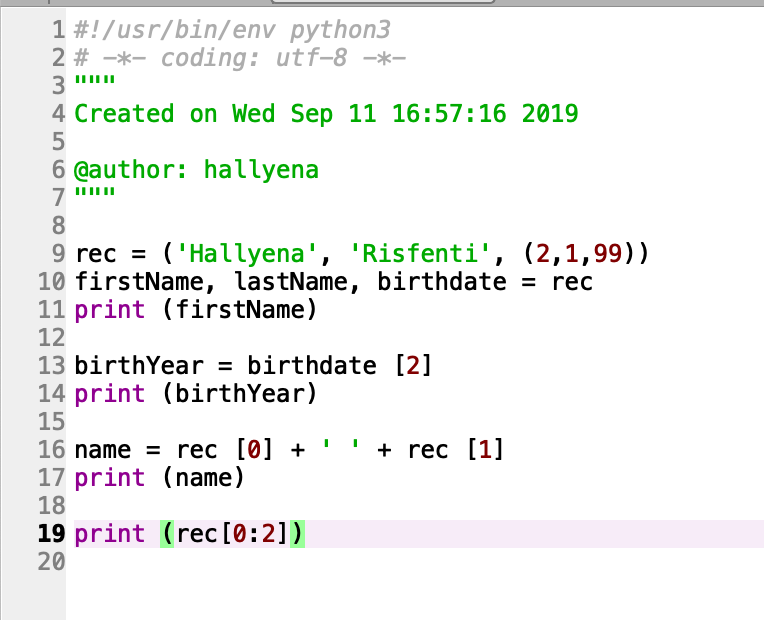
Dipenghujung kelas, para mahasiswa mempelajari lebih dalam mengenai Python. Hal awal yang kami lakukan adalah membuat "Hello world" menggunakan bahasa pemrograman Python. Selanjutnya kami membahas mengenai Tuple dan List. Saya mencoba kembali dua materi tersebut menggunakan aplikasi Anaconda, lebih spesifiknya lagi Spyder. Spyder memudahkan saya untuk run Python karena fiturnya yang sudah lengkap. Berikut merupakan Tuple dan List yang telah saya coba:
Tuple
Setelah di run, berikut hasilnya:
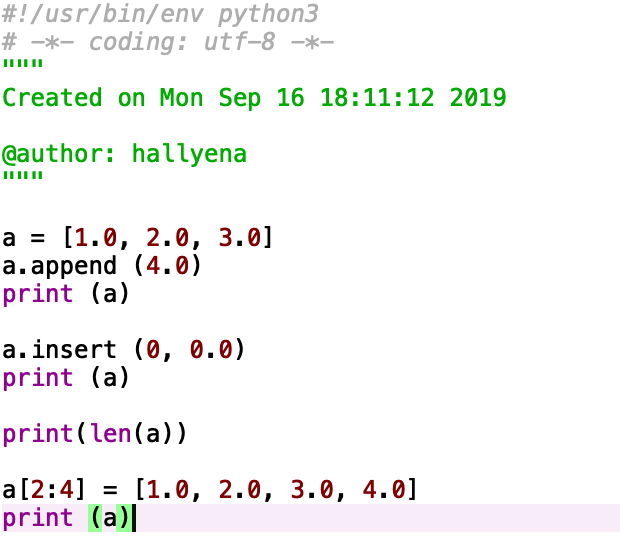
List
Setelah di run, berikut hasilnya:
Pertemuan Ketiga
Hari, Tanggal : Rabu, 18 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
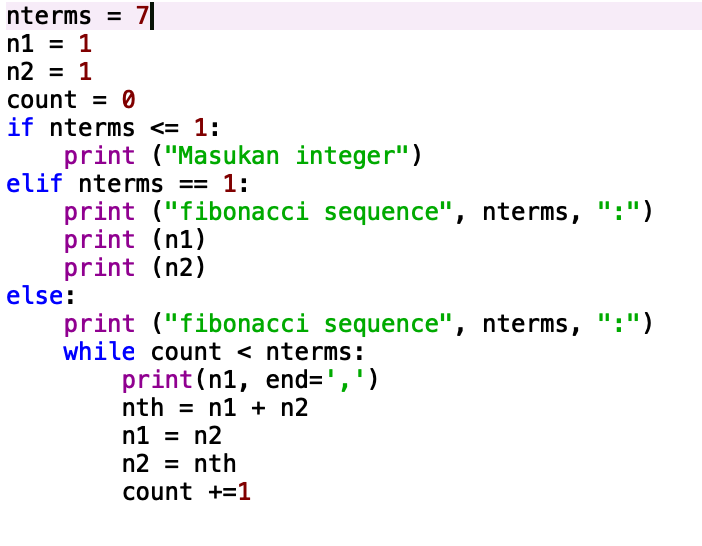
Pertemuan kali ini, diadakannya quiz untuk membuat algoritma, flowchart, serta bagaimana cara penulisannya pada Python. Soal yang diberikan berkaitan dengan fibonacci sequence. Fibonacci sequence yang diberikan adalah sebagai berikut 1,1,2,3,5,8,13,...n. Sequence ini dapat diselesaikan atau didapatkan dengan dua cara yaitu:
1. Menyelesaikan fibonacci sequence dengan menggunakan if else statement dan while loop.
Berikut caranya:
Untuk mencoba atau menjalankan program ini, value nterms harus diubah dan ini merupakan hasil yang didapatkan:
2. Menyelesaikan fibonacci sequence dengan menggunakan metode fungsi recursion. Fungsi recursion digunakan untung mengkalkulasi nth term pada sequence
Berikut caranya:
Hasil yang didapatkan adalah sebagai berikut:
Pertemuan Keempat
Hari, Tanggal : Rabu, 25 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pada pertemuan kali ini, kami diperkenalkan oleh model atau permodelan. Di kelas kami berkolaborasi dalam memaknai apa itu model dengan kolom comment yang telah disediakan.
Model menurut saya adalah
Model itu adalah representasi atau bentuk nyata dari suatu sistem atau objek yang ingin diuji. Pemodelan ini dapat memudahkan dalam eksperimen serta pengujian hingga pada akhirnya mendapatkan suatu hasil dengan performa terbaik.
Setelah semua mahasiswa mengisi kolom comment, didapatkan bahwa pengertian model mengandung 3 hal yang utama, yaitu: 1. Simplifikasi 2. Representasi 3. Asumsi
Modelling adalah sebuah simplifikasi atau representasi yang mensimplifikasi. Objek atau sistem merupakan representasi sederhana dari suatu keadaan nyata yang rumit. Kita perlu menghitung agar dapat memastikan apa yang sudah kita design itu berfungsi dan bekerja dengan baik. Parameternya antara lain adalah kuat dan dapat menahan beban secara optimal sehingga disinilah gunanya simplifikasi.
Modelling juga merupakan asumsi, sebagai contoh terdapat penampang yang dibawahnya materialnya dari batu. Contoh lainnya adalah alat-alat mesin pasti memiliki fondasi atau ada yang menampang sehingga yang kita coba atau kita uji adalah apakah alat tersebut dapat berfungsi atau tidak.
Pertemuan Kelima
Hari, Tanggal : Rabu, 2 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Suatu permasalahan dapat dibuat pemodelannya dikarenakan pemodelan ini dapat memudahkan manusia/user dalam menyelesaikan masalah. Salah satu problem solvernya adalah dengan menggunakan bahasa pemrograman python.
Alasan bahasa pemrograman python ini seringkali dijadikan pilihan untuk menyelesaikan masalah antara lain karena python gratis dan saat ini sering digunakan dalam industry 4.0. Keuntungan lain yang didapatkan dari penggunaan bahasa python itu sendiri ialah python mudah untuk di download dan install karena sudah tersedia di seluruh major operating system. Ditambah pula python mudah untuk dipelajari dan dimengerti.
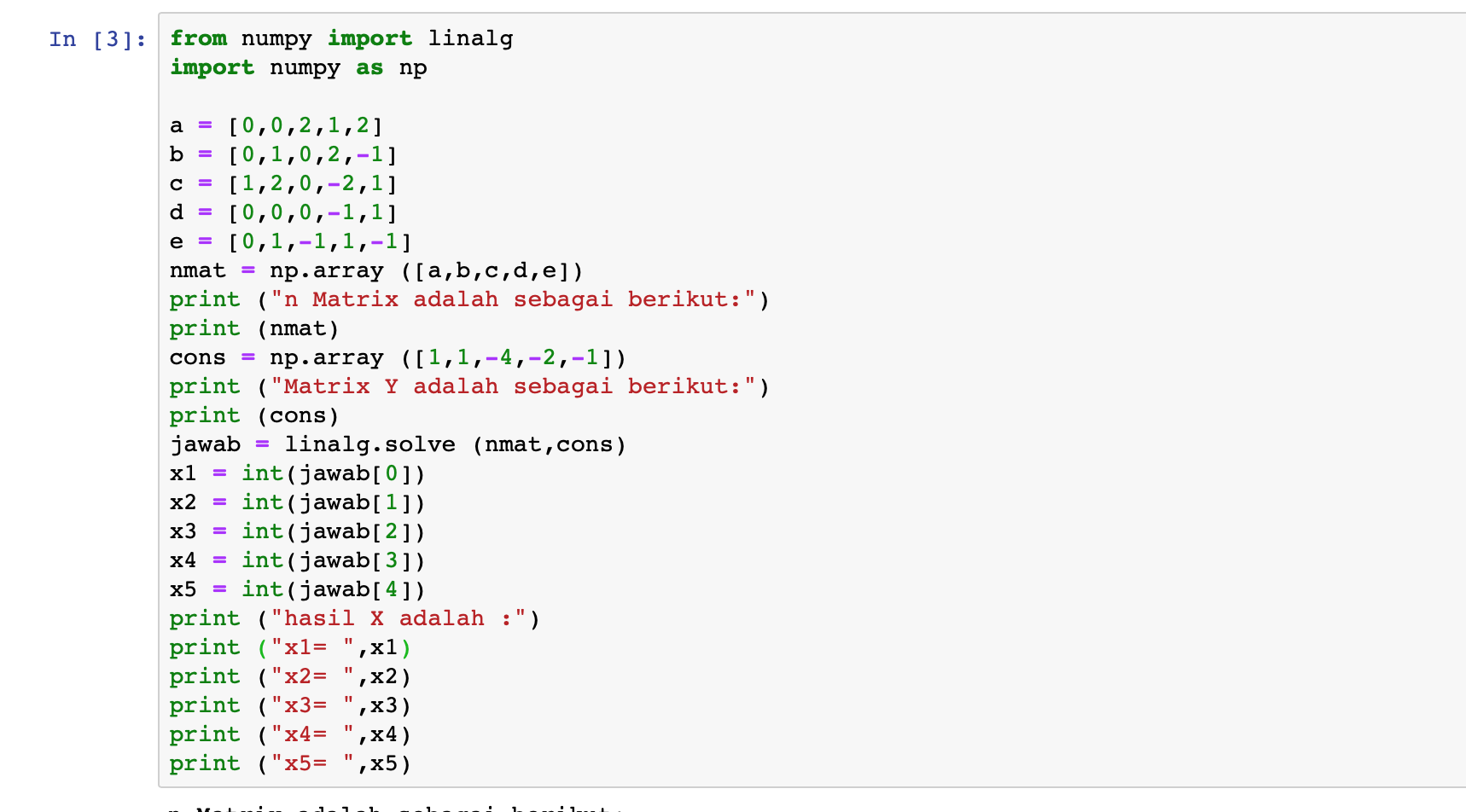
Pertemuan kali ini diisi oleh asisten dosen dan kami mempelajari mengenai aplikasi aljabar linear khususnya gaussian elimination pada sistem pegas. Materi ini berkaitan dengan Finite Element Method (FEM).
Finite Element Method (FEM) itu sendiri merupakan numerical technique untuk menyelesaikan masalah-masalah fenomena physical yang complex. Fenomena-fenomena ini terbagi lagi kedalam beberapa kategori. Namun, karena contoh pemodelan yang digunakan adalah pegas maka fenomena physical yang digunakan merupakan solid mechanics.
Kemudian asisten dosen menjelaskan tentang penggunaan pemodelan pada sistem tunggal untuk menjadi persamaan linier dengan cara menerjemahkan rumus yang biasa digunakan pada pegas menjadi sebuah matrix. Selain itu, variasi yang digunakan tidak hanya untuk matrix pegas yang tunggal melainkan juga pemodelan sistem ganda pada pegas seri dengan menggunakan superposisi matrix.
Pada pemodelan kali ini juga diajarkan pula penggunaan modul yang bertujuan untuk memudahkan perhitungan sistem dengan gaussian elimination. Modul yang digunakan antara lain adalah: Numpy dan Sympy
Pertemuan Keenam
Hari, Tanggal : Rabu, 9 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pada pertemuan kali ini kami belajar mengenai cara memecahkan masalah menggunakan persamaan aljabar linear dan dijelaskan bahwa satu set itu memiliki banyak sekali penyelesaikan masalahnya.
Berikut merupakan cara-cara atau langkah-langkah dalam penyelesaian aljabar: 1. Metode eliminasi dengan cara mengurangi variable dari persamaan berikutnya. Hal ini dilakukan untuk mendapatkan satu varible yang selanjutnya digunakan untuk langkah substitusi. 2. Gauss 3. Trial and Error
Peran komputer dalam mata kuliah ini adalah dalam pembuatan pemodelan matematika tetapi logika tetap dari manusia dan peran komputer hanya membantu perhitungannya.
Permodelan matematis ini bentuknya adalah differential. Persamaan ini ada karena masalah yang kita hadapi itu terjadi secara kontinu.
Kontinu assumption : salah satu contohnya adalah satu ruangan itu dipenuhi dengan oksigen sehingga tidak adanya ruang hampa dalam ruangan. Oleh karena itu kita dapat menghitung temperature di titik mana pun dalam ruangan tersebut.
Jika kontinu assumption ini diberi gaya maka setiap titik akan merasakan beban maka setiap titik akan berdislokasi atau berpindah tempat. Selisih perpindahan itu biasa kita sebut dengan displacement (u). Limit ketiga delta u menuju 0 adalah ketika perubahan displacement disebut dengan (du). Hasil differential itu sangat kecil tetapi tidak mencapai angka 0.
Materi kali ini mengajarkan mahasiswa untuk menjadi mahasiswa yang cerdas dalam artian selalu memikirkan kedepan atau langkah selanjutnya.
Pertemuan Ketujuh
Hari, Tanggal : Rabu, 16 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
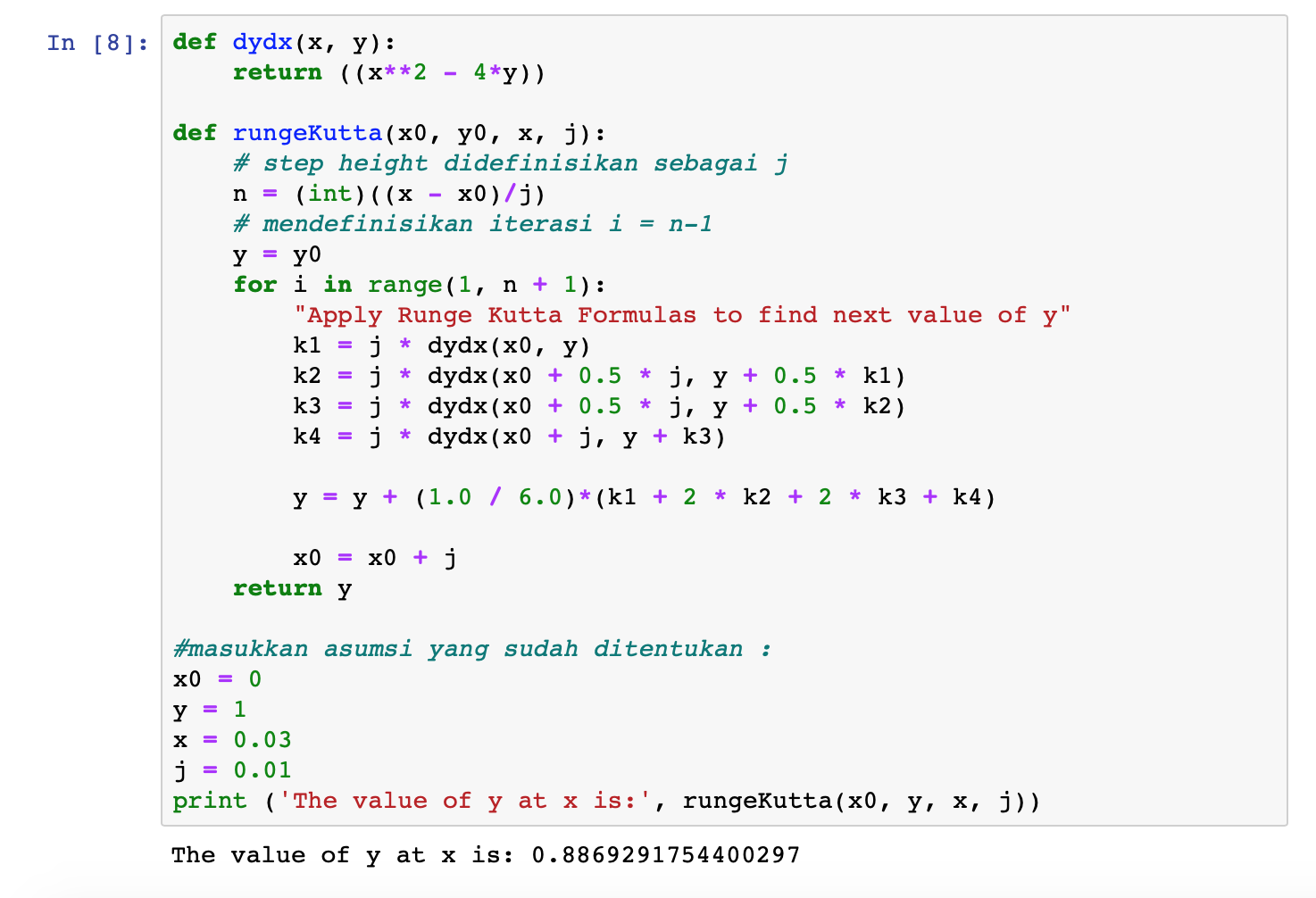
Pada pertemuan kali ini kami melaksanakan kuis sebagai acuan dan sarana kami mempersiapkan UTS yang akan datang yaitu mengenai Gaussian Elimination dan juga Runge Kutta Fourth Order. Berikut adalah soal yang diberikan dari buku Jaan Kiusalaas - Numerical Methods
Saya menyelesaikan soal mengenai penulisan algoritma penyelesaian gaussian elimination dan juga hasil pada kertas soal yang diberikan, sedangkan codingnya adalah sebagai berikut:
Soal yang selanjutnya adalah mengenai Runge Kutta Fourth Order yang ada di bab 7. Berikut soalnya:
Lalu berikut coding pythonnya:
UTS Metnum
Hari, Tanggal : Rabu, 23 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
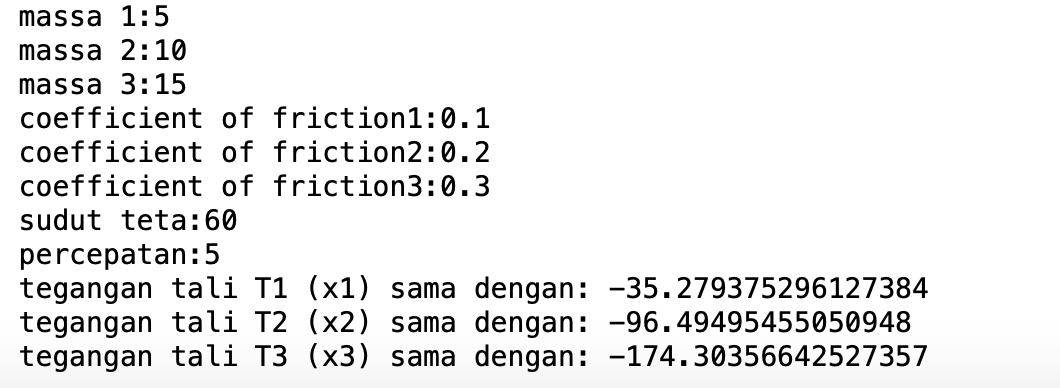
Hari ini kami mengerjakan soal UTS yang diberikan oleh Pak Dai yaitu untuk soal IA mencari tegangan tali dengan metoda numerik.
Berikut adalah codingan yang telah saya buat beserta asumsi-asumsinya:
from math import*
g = 9.81
m1 = eval(input("massa 1:"))
m2 = eval(input("massa 2:"))
m3 = eval(input("massa 3:"))
k1 = eval(input("coefficient of friction1:"))
k2 = eval(input("coefficient of friction2:"))
k3 = eval(input("coefficient of friction3:"))
teta = eval(input("sudut teta:"))
a = eval(input("percepatan:"))
s = sin (teta)
c = cos (teta)
x1 = m1*g*(s - k1*c) - m1*a
x2 = m2*g*(s - k2*c) + x1 - m2*a
x3 = m3*g*(s - k3*c) + x2 - m3*a
print("tegangan tali T1 (x1) sama dengan:",x1)
print("tegangan tali T2 (x2) sama dengan:",x2)
print("tegangan tali T3 (x3) sama dengan:",x3)
Hasil yang didapatkan berdasarkan codingan diatas adalah:
Selanjutnya kami diberikan tugas untuk membuat video mengenai penyelesaian dengan bahasa Python yang kami buat masing-masing. Berikut adalah video penyelesaian persoalan 1A yang telah saya buat:
Soal IB diberikan gambar mobil dan membuat model matematis (persamaan differensial) untuk keseimbangan dinamis sesuai dengan gambar mobil. Kami harus mencari waktu yang diperlukan oleh mobil dari keadaan diam hingga mencapai top speednya. Berikut bahasa python yang saya tulis untuk mendapatkan waktu yang diperlukan oleh mobil:
from math import *
from sympy import *
g = 9.81
density = 1.2 #merupakan massa jenis (density) udara
cd = eval(input("drag coefficient:"))
area = eval(input("luas (m^2):"))
v1 = eval(input("kecepatan akhir:"))
m = eval(input("massa mobil(kg):"))
u = eval(input("koefisien gesek:"))
a = eval(input("percepatan(m/s^2)"))
fs = g*u
f1 = a
for v0 in range (0,v1):
fdrag = (cd*area*density*v0**2)/2*m
atot = f1 - (fdrag + fs)
t = -(v1)/atot
print("percepatan total (m/s^2):", atot)
print("waktu yang diperlukan oleh v1:", t)
Setelah memasukkan atau measumsikan data-data yang diperlukan untuk menyelesaikan permasalahan diatas, jawaban yang didapat adalah sebagai berikut:
Selanjutnya kami diberikan tugas untuk membuat video mengenai penyelesaian dengan bahasa Python yang kami buat masing-masing. Berikut adalah video penyelesaian persoalan 1B yang telah saya buat:
Perbaikan UTS
Berikut merupakan coding menggunakan bahasa python dengan metode rungke kutta untuk mendapatkan top speed mobil:
g = 9.81
u = eval(input("Koefisien gesek : "))
a = eval(input("Percepatan mobil : "))
cd = eval(input("Drag coefficient : "))
m = eval(input("Massa mobil : "))
t0 = 0
v0 = 0
dt = 1
error = 100
F = a - g*u #dibagi dengan massa fs = cd/m #dibagi dengan massa
lst = []
def dvdt(t0, v0):
return F-(fs*(v0)**(1.5))
while error > 0.005:
k1 = dvdt(t0, v0)
k2 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k1)
k3 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k2)
k4 = dvdt(t0 + dt, v0 + dt * k3)
v1 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
t0 = t0 + dt
error = ((v1 - v0) / v1)*100 #persentase error
v0 = v1
lst.append(v1)
waktu = len(lst)
print ("Waktu yang dibutuhkan mobil untuk mencapai kecepatan maksimal: ", waktu+1, "s")
print ("Kecepatan maksimal(top speed) mobil: ", v1, "m/s")
Kemudian berikut adalah asumsi yang saya buat beserta hasil yang didapat dari pemrograman diatas
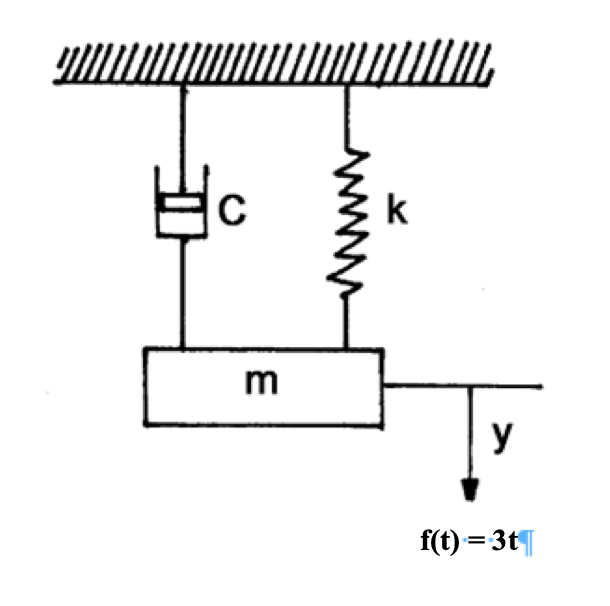
Pemodelan Matematika dengan Metode Runge Kutta Orde 4
Berikut adalah persamaan sistem yang sesuai dengan gambar diatas:
F = m*a (sigma Gaya) 3t - cv = m*a a = (3t-cv)/m dv/dt = (3t-cv)/m
Dan berikut penyekesaiannya menggunakan bahasa pemrograman Python:
def DiferensialV(t, v): #DiferensialV merupakan fungsi turunan V terhadap t
return ((3*t - c*v)/m)
m=eval(input("Massa objek (kg) : "))
c=eval(input("Damping coefficient (Ns/m) : "))
t0 = 0 #t awal
v0 = 0 #v awal
t = 10 #kecepatan sistem yang dibutuhkan setelah mencapai waktu 10 detik
h = 0.1 #delta yang digunakan
nilai = (int)((t - t0)/h) #menghitung jumlah increment
for i in range(1, nilai + 1):
k1 = h * DiferensialV(t0, v0) #runge kutta
k2 = h * DiferensialV(t0 + 0.5 * h, v0 + 0.5 * k1)
k3 = h * DiferensialV(t0 + 0.5 * h, v0 + 0.5 * k2)
k4 = h * DiferensialV(t0 + h, v0 + k3)
v0 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #sigma nilai k1,k2,k3,k4 ke y' yang baru dan dibagi
t0 = t0 + h
print("Kecepatan sistem pegas: ",v0, "m/s")