Difference between revisions of "Stefanus Nandiwardhana Mahardhika"
| Line 245: | Line 245: | ||
<comments voting"plus" /> | <comments voting"plus" /> | ||
| + | |||
| + | '''Torpedo Calculation''' | ||
| + | Dilakukan analisis terhadap torpedo Mark 48 | ||
| + | from math import* | ||
| + | import pandas as pd | ||
| + | from matplotlib import pyplot as plt | ||
| + | #Data from Mark 48 Torpedo | ||
| + | Fthrust = 20000 | ||
| + | DragCoef = 0.22 | ||
| + | LiftCoef = 0.3 | ||
| + | Rho = 1000 | ||
| + | r = 0.265 | ||
| + | A = 3.14*r**2 | ||
| + | Afin = 0.2 | ||
| + | m = 1558 | ||
| + | Vol = 1.22 | ||
| + | alphadegrees = 30 | ||
| + | alpha = alphadegrees*3.14/180 | ||
| + | g = 9.81 | ||
| + | vx0 = 0 | ||
| + | vy0 = 0 | ||
| + | hx = 0.1 | ||
| + | tx0 = 0 | ||
| + | error = 100 | ||
| + | lstx = [] | ||
| + | def dvxdt(tx0,vx0): | ||
| + | return((Fthrust*cos(alpha) - 0.5*DragCoef*Rho*A*vx0**2)/m) | ||
| + | while error > 0.1: | ||
| + | k1 = hx * dvxdt(tx0,vx0) | ||
| + | k2 = hx * dvxdt(tx0 + 0.5 * hx, vx0 + 0.5 * k1) | ||
| + | k3 = hx * dvxdt(tx0 + 0.5 * hx, vx0 + 0.5 * k2) | ||
| + | k4 = hx * dvxdt(tx0 + hx, vx0 + k3) | ||
| + | vx1 = vx0 + (1.0/6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | tx0 = tx0 + hx | ||
| + | error = ((vx1 - vx0)/vx1)*100 | ||
| + | vx0 = vx1 | ||
| + | lstx.append(vx1) | ||
| + | tx = len(lstx) | ||
| + | lstx.append(vx1) | ||
| + | |||
| + | hy = 0.1 | ||
| + | ty0 = 0 | ||
| + | error = 100 | ||
| + | lsty = [] | ||
| + | def dvydt(ty0,vy0): | ||
| + | return((Fthrust*sin(alpha) + Rho*((Vol*g) + 0.5*LiftCoef*Afin) - m*g - | ||
| + | 0.5*DragCoef*Rho*A*vy0**2)/m) | ||
| + | while error > 0.1: | ||
| + | g1 = hy * dvydt(ty0,vy0) | ||
| + | g2 = hy * dvydt(ty0 + 0.5 * hy, vy0 + 0.5 * g1) | ||
| + | g3 = hy * dvydt(ty0 + 0.5 * hy, vy0 + 0.5 * g2) | ||
| + | g4 = hy * dvydt(ty0 + hx, vy0 + k3) | ||
| + | vy1 = vy0 + (1.0/6.0)*(g1 + 2 * g2 + 2 * g3 + g4) | ||
| + | ty0 = ty0 + hy | ||
| + | error = ((vy1 - vy0)/vy1)*100 | ||
| + | vy0 = vy1 | ||
| + | lsty.append(vy1) | ||
| + | ty = len(lsty) | ||
| + | lsty.append(vy1) | ||
| + | |||
| + | print("Time required to reach max horizontal velocity: ", tx+1, "seconds") | ||
| + | print("Maximum Horizontal Velocity: ", vx1, "m/s") | ||
| + | print("Time required to reach max vertical velocity: ", ty+1, "seconds") | ||
| + | print("Maximum Vertical Velocity: ", vy1, "m/s") | ||
| + | |||
| + | lstxr = [round(u,2) for u in lstx] | ||
| + | graphx = list(range(1,tx+2)) | ||
| + | plt.plot(graphx,lstxr) | ||
| + | plt.title("Horizontal Velocty Graph") | ||
| + | plt.ylabel("Horizontal Velocity (m/s)") | ||
| + | plt.xlabel("Time (seconds)") | ||
| + | plt.show() | ||
| + | |||
| + | lstyr = [round(i,2) for i in lsty] | ||
| + | graphy = list(range(1,ty+2)) | ||
| + | plt.plot(graphy,lstyr) | ||
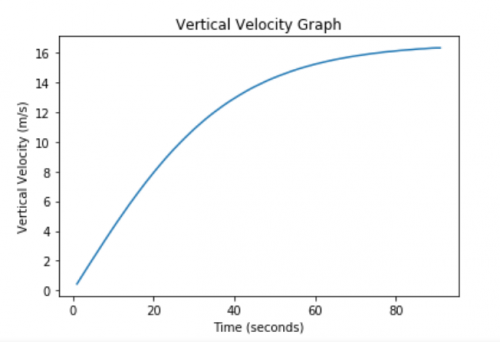
| + | plt.title("Vertical Velocity Graph") | ||
| + | plt.ylabel("Vertical Velocity (m/s)") | ||
| + | plt.xlabel("Time (seconds)") | ||
| + | plt.show() | ||
| + | |||
| + | '''Output:''' | ||
| + | Time required to reach max horizontal velocity: 63 seconds | ||
| + | Maximum Horizontal Velocity: 26.418908231173756 m/s | ||
| + | Time required to reach max vertical velocity: 91 seconds | ||
| + | Maximum Vertical Velocity: 16.32477384211023 m/s | ||
| + | [[File:Torpedo_Horizontal_Velocity_Graph.png|500px]] | ||
| + | [[File:Torpedo_Vertical_Velocity_Graph.png|500px]] | ||
Revision as of 00:14, 6 November 2019
Introduksi
Perkenalkan, nama saya Stefanus Nandiwardhana Mahardhika (Akrab dipanggil Evan). Saya adalah mahasiswa Teknik Mesin di Universitas Indonesia angkatan 2017. Saya adalah salah satu dari sekian banyak mahasiswa rantau di Universitas Indonesia. Saya lahir di Kota Yogyakarta pada tanggal 25 Februari 1999.
Nama: Stefanus Nandiwardhana Mahardhika Jurusan: Teknik Mesin Angkatan: 2017 NPM: 1706036160
Kenapa Anak Teknik Mesin Harus Belajar Kalkulus?
Menurut saya kalkulus adalah salah satu ilmu yang mendasar dalam ilmu ke-Teknik-an. Tidak jarang dalam memecahkan sebuah masalah, baik yang kompleks maupun yang sederhana, kita sebagai orang teknik memerlukan ilmu kalkulus. Dari memplot grafik sampai menghitung efisiensi sebuah pembangkit listrik tenaga uap, terdapat banyak hal yang tidak bisa terlepas dari penggunaan ilmu kalkulus.
Pertemuan Pertama
Pada pertemuan pertama mata kuliah metode numerik ini, saya dikenalkan dengan Dr. Ahmad Indra dan Dr. Eng. Radon Dhelika. Kuliah diawali dengan penjelasan singkat akan mata kuliah Metode Numerik oleh Pak Dai. Beliau juga menjelaskan akan sistem penilaian di kelas ini yang lebih melihat kepada perkembangan yang dialami oleh mahasiswa selama mengikuti mata kuliah ini. Hal ini dikarenakan kepercayaan Pak Dai dan Pak Radon terhadap continuous learning. Pak Radon kemudian menambahkan alasan penggunaan bahasa koding Python dalam pembelajaran mata kuliah ini yang berupa semakin populernya penggunaan bahasa Python dalam berbagai hal. Hal ini memudahkan mahasiswa dalam mencari informasi bantuan dalam mempelajarinya.
Tugas 2: *Pelajari Python *Buatlah sebuah program untuk memecahkan soal limit (x^2 - 1)/(x - 1) dengan algoritma flowchart/kata-kata. *Tulis aplikasi dari metode numerik
Tugas 1
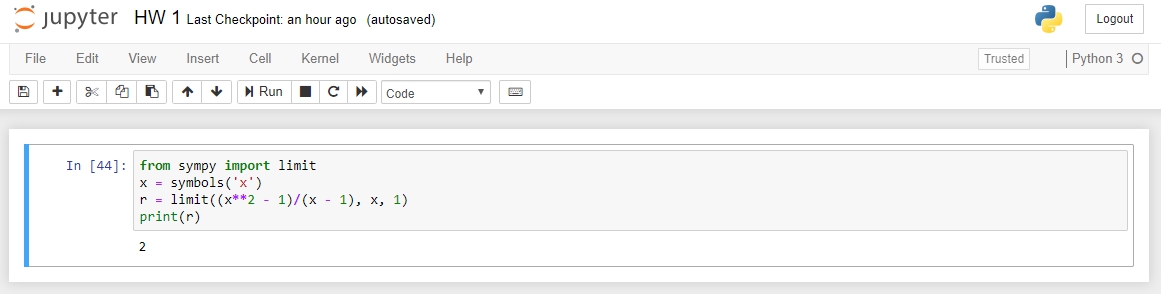
1. Pemecahan soal limit (x^2 - 1)/(x - 1) ternyata tidaklah gampang. Awalnya saya mencoba-coba berusaha membuat koding sendiri dari awal tanpa bantuan library. Namun, setelah mencoba-coba dan gagal, akhirnya saya memutuskan untuk menggunakan bantuan Sympy Library. Berikut hasilnya:
Penggunaan Sympy Library sangatlah mempersingkat dan menyederhanakan koding yang perlu ditulis.
Saya menggunakan Jupyter Notebook sebagai interface editor dalam menulis koding Python dengan bantuan Anaconda Navigator sebagai launcher-nya.
Line 1: Koding yang saya tulis diawali dengan "from sympy import limit" untuk melakukan impor modul simpy yang berhubungan dengan limit. Saya juga bisa menggunakan "*" untuk menggantikan "limit" untuk mengimpor semua modul dan membiarkannya mencari sendiri modul yang berhubungan.
Line 2: Kemudian saya menetapkan x sebagai simbol x yang ada di simpy
Line 3: Kemudian saya menetapkan sebuah karakter acak ("r") untuk ditetapkan sebagai persamaan yang ingin dicari (limit (x^2 - 1)/(x - 1)). Setelah penulisan persamaan, saya memberi tanda koma untuk menuliskan variabel dan angka yang didekati.
Line 4: Terakhir, saya memerintahkan agar jawaban dari persamaan tadi dicetak.
Jawaban yang didapatkan adalah 2.
2. Aplikasi dari metode numerik tentunya sangat banyak, mengingat metode numerik adalah salah satu cara pemecahan permasalahan perhitungan matematika dengan solusi yang berupa perkiraan sehingga penyelesaiannya cenderung lebih sederhana daripada metode analitik. Berikut adalah contoh aplikasi dari metode numerik:
- Penyelesaian persamaan diferensial
- Regresi
- Interpolasi
- Integrasi Numerik
- Differensiasi Numerik
Semuanya tentunya sangat dibutuhkan dalam banyak bidang, terutama bidang ke-teknik-an.
Pertemuan Kedua
Pada pertemuan kedua, kami membahas komputer sebagai media menulis coding. Pak Dai menggunakan permainan komputer catur sebagai sebuah contoh. Mengapa google ads dapat mengetahui kebutuhan kita saat itu? Apa yang membuat database google lebih luas daripada database otak kita. Perbedaan 32 bit dan 64 bit adalah jumlah interger yang bisa dibaca oleh komputer tersebut. 32 bit berarti komputer tersebut dapat membaca 2^31 interger. Komputer secara fisik hanya mengenal on (1) dan off (0), atau yang disebut sebagai binary code. OS yang mampu menjalankan software 32 bit berarti dia dapat membaca sekian binary code. Apabila terdapat lebih maka dia akan mengalami overflow. Sedangkan 64 bit mempresentasikan angka paling kecil dan paling besar lebih banyak lagi sehingga lebih cepat dan lebih akurat daripada 32 bit. Processor 32 bit dapat membaca 4GB RAM, sedangkan 64 bit processor dapat membaca sampai 16 milyar GB RAM. 5.0 adalah pancasila karena teknologi harus empowering human. Jangan sampai teknologi malah menjadi melemahkan manusia. Jangan sampai manusia di-drive oleh teknologi seperti sosial media dll. Kita yang harus bisa me-drive teknologi. Hal ini dapat dilakukan salah satunya sebagai orang mesin adalah mengerti numerik software yang kita gunakan dalam bidang engineering.
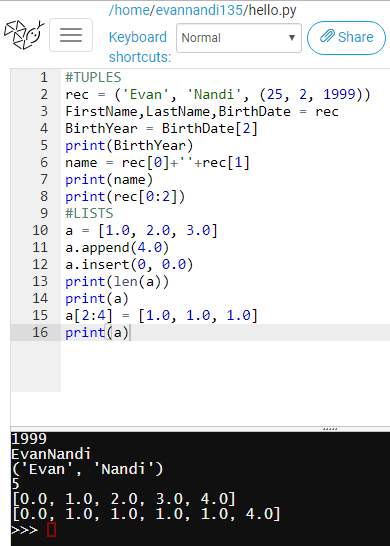
Kami kemudian diberikan pelajaran akan dasar-dasar python oleh Pak Radon. Karena keterbatasan program pada komputer kampus, kami terpaksa menggunakan website pythonanywhere.com sebagai media untuk menulis koding python. Di situ kami belajar untuk mencetak "Hello Python World" sampai beberapa koding yang berupa Tuples dan Lists. Berikut adalah hasil percobaan saya menggunakan Tuples dan Lists.
Setiap software engineering dilakukan melalui trial and error.
Numerical methods in engineering with python 3
Minggu depan jam 4 sore quiz tentang pemrograman
Pertemuan Ketiga
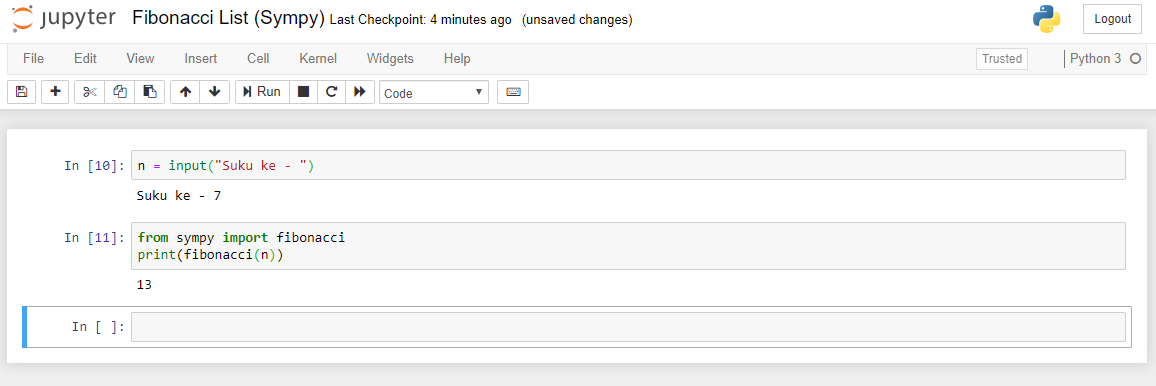
Pertemuan ketiga dimulai dengan quiz mengenai coding. Permasalahan yang harus kami pecahkan berupa pembuatan program yang dapat menentukan suku ke-n dari deret fibonacci. Karena bingung bagaimana saya bisa menyelesaikan masalah tersebut, pada saat quiz saya memilih untuk menggunakan library sympy. Namun, ternyata setelah quiz selesai Pak Radon mengatakan bahwa penggunaan library tidak diperbolehkan. Berikut adalah coding yang saya tulis:
Kami pun kemudian disuruh untuk mengulang pengerjaan quiz tetapi dengan petunjuk dari Pak Radon dan Pak DAI bahwa penyelesaiannya bisa menggunakan function atau loop. Berikut adalah hasilnya.
Penyelesaian dengan Function:Penyelesaian dengan Loop:
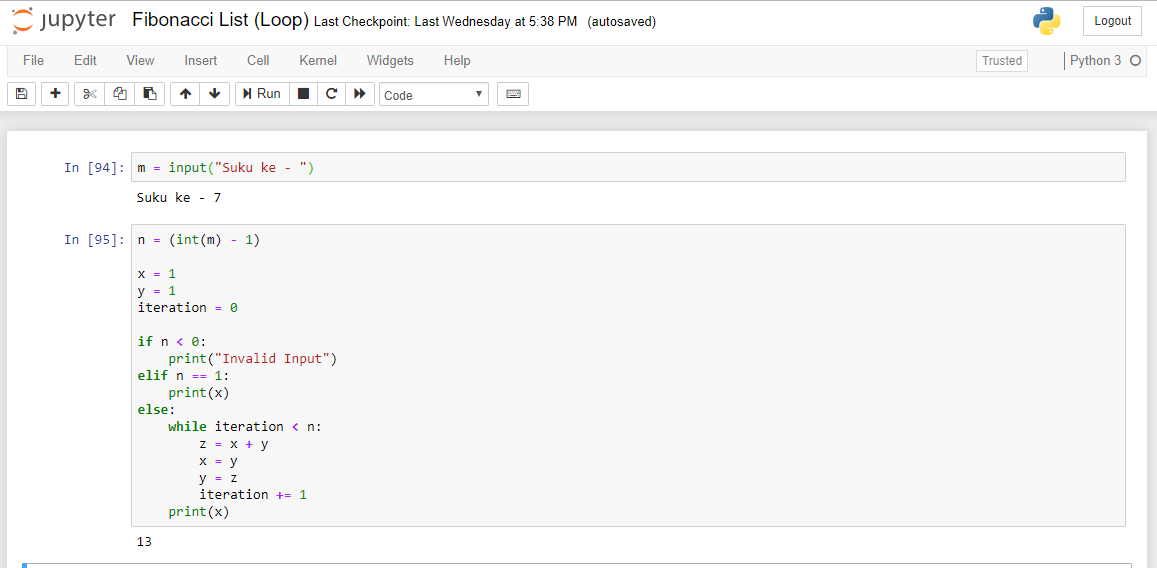
Tugas 1: Kerjakan fibonacci sequence dengan loop (for/while) dan function/subroutine.
Tugas 2: Presentasi Kelompok contoh soal eliminasi gauss bab 2 pada buku Num. Meth in Eng. using python (J. Kiusalaas)
Pertemuan Keempat
Pada pertemuan keempat, kami pertama membahas tentang Pemodelan Komputer (Computer Moelling). Pertama-tama kami disuruh menyebutkan apa itu "model" menurut kami. Menurut saya sendiri, model adalah suatu gambaran yang mewakili suatu sistem atau objek. Penggunaan model akan memudahkan analisis sistem atau objek tersebut. Setelah masing-masing mahasiswa menyebutkan arti "model" menurut mereka masing-masing, Pak Dai kemudian menyebutkan bahwa ada tiga poin dari sebuah model, yaitu: Representasi, simplifikasi, dan asumsi. Simulasi komputer tidak pernah mencapai keakuratan 100% karena simulasi hanyalah sebuah pendekatan (Asumsi). Contoh dari asumsi adalah analisis sebuah fondasi yang dilakukan menggunakan rumus stress. Analisis dilakukan dengan mengasumsikan modulus elastisitas dari setiap titik. Simplifikasi adalah sebuah penyederhanaan. Contohnya, analisis fondasi yang kita buat tadi kita buat menjadi analisis satu dimensi.
Elastisitas: keengahan untuk berubah bentuk
Tensor flow dalam AI google Pengembang google menevelop engine mesin learning menggunakan python jadi python tuh suatu hal yang sangat biasa.
Tugas 1: Membangun persamaan aljabar displacement dari sebuah batang dalam kesetimbangan pada 4 titik
Pertemuan Kelima
Pada pertemuan kelima, kami diberi penjelasan oleh asisten dosen mengenai aljabar simultan. Kami diberi contoh modelling spring system yang berupa beberapa pegas yang dihubungkan dalam formasi seri, kemudian kami diberi penjelasan cara modellingnya dalam bentuk matriks dan cara melakukan superposisi pada matriks tersebut sehingga kami dapat melakukan modelling pada spring system yang memiliki lebih banyak pegas. Modelling matriks ini nantinya akan diselesaikan menggunakan metode Gauss Jordan dalam Python. Saat menggunakan input, eval harus digunakan sehingga menjadi angka, tanpa eval dia akan menganggapnya sebagai string. Syntax eval juga dapat diubah menjadi int (interger) atau float untuk angka dengan desimal.
Pertemuan Keenam
Peran komputer dalam pemecahan masalah hanya.... modelling harus dari kita. Mungkin sebaiknya nama mata kuliah Metode Numerik diganti "Computer Aided Engineering" Karena komputer dapat membantu kita dalam memecahkan masalah engineering apabila sudah kita tentukan dan tuliskan modellingnya. Sifat continuum artinya pada saat benda tersebut mengalami gaya maka gaya tersebut akan diteruskan ke semua bagian benda tersebut. Selain itu, semua titik benda tersebut memiliki sifat yang dapat diukur. Masalah atau benda yang kita deal with, semuanya bersifat continuum sehingga memiliki model matematika dalam bentuk persamaan-persamaan differensial yang dapat kita pecah dengan Metode Numerik. Sifat discontinuum baru akan kita jumpai pada skala molekuler.
Setelah itu Bang Edo menjelaskan tentang metode Runge-Kutta. Metode ini adalah salah satu cara penyelesaian persamaan differensial. Runge-Kutta Method terdiri dari 2nd order, 3rd order, dan 4th order, dimana 4th Order Runge-Kutta Method adalah metode yang paling akurat. Runge-Kutta ini digunakan untuk penyelesaian masalah yang sudah dalam bentuk modelling matematika, tetapi susah untuk diselesaikan menggunakan metode eksak.
Quiz 2
Soal 1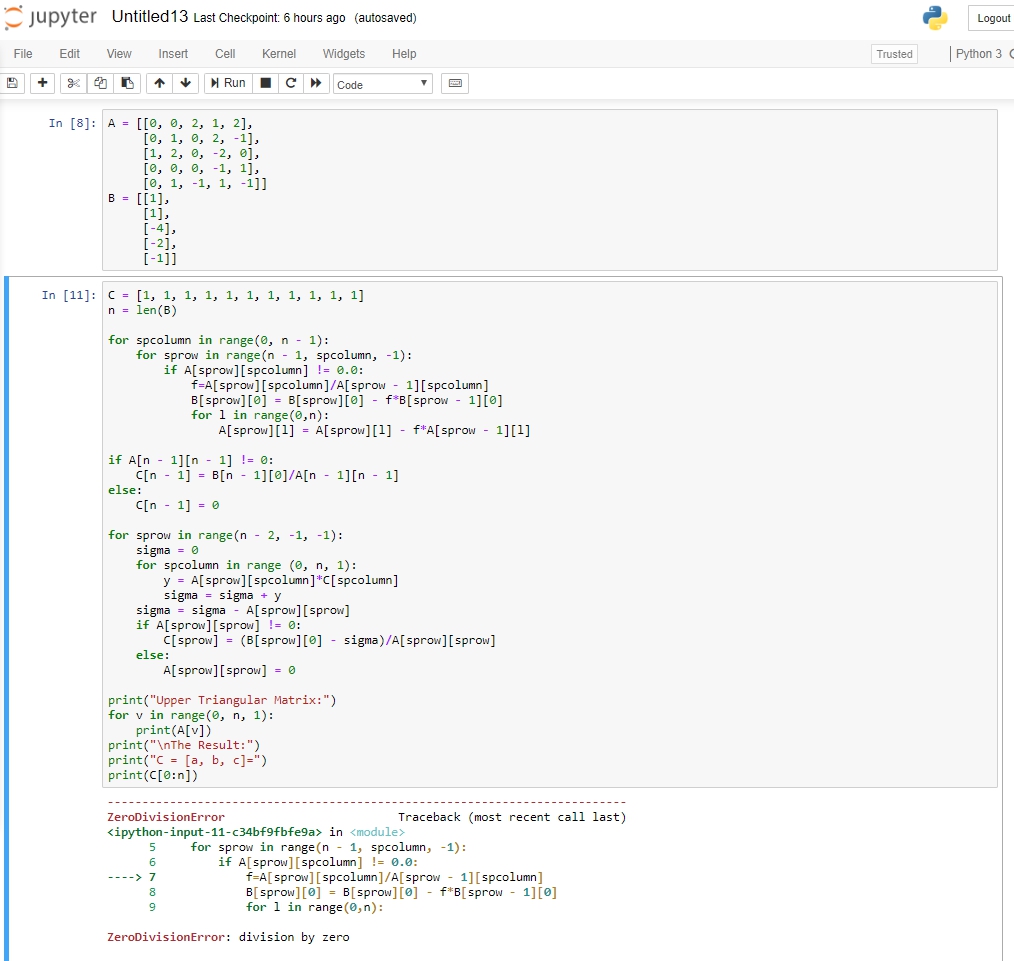
Soal 1 Setelah Revisi
Soal 2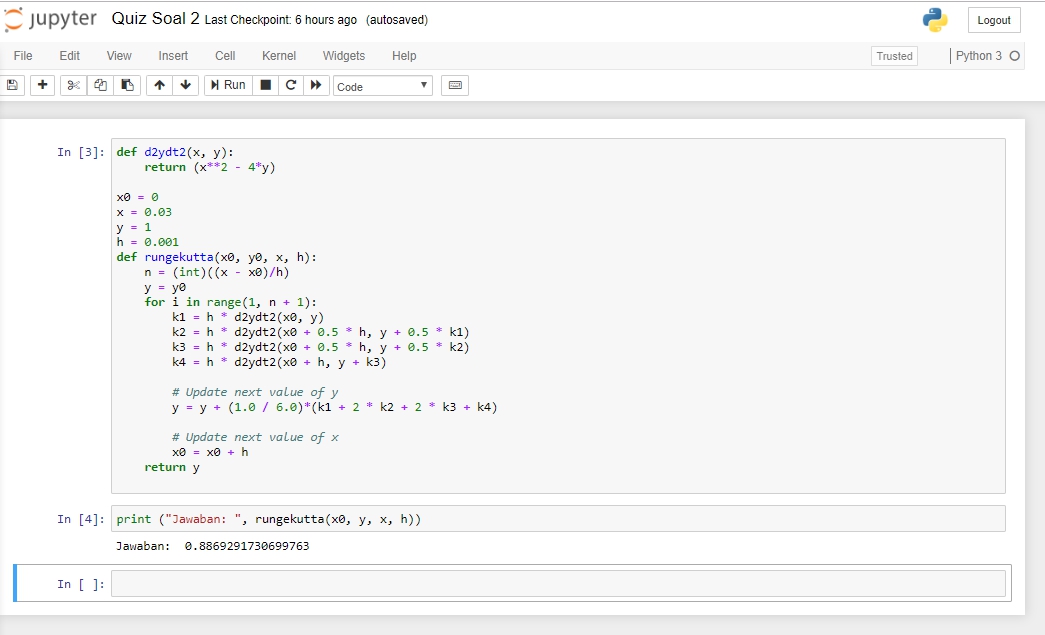
UTS
Video Muhasabah
Soal 1
from math import *
g = 9.81
m1 = float(input("Massa 1: "))
m2 = float(input("Massa 2: "))
m3 = float(input("Massa 3: "))
u = float(input("Friction Coefficient: "))
teta = float(input("sudut teta: "))
a = float(input("percepatan: "))
t1 = m1*g*((sin (teta))+u*(cos (teta))) - m1*a
t2 = m2*g*((sin (teta))+u*(cos (teta))) + t1 - m2*a
t3 = m3*g*((sin (teta))+u*(cos (teta))) + t2 - m3*a
m4 = -t3/(a+g)
print ("Massa 4: ",m4," kg")
print ("Tegangan Tali 1:", t1, "N")
print ("Tegangan Tali 2:", t2, "N")
print ("Tegangan Tali 3:", t3, "N")
Result:
Massa 4: 60.11978934383861 kg
Tegangan Tali 1: -187.6557242836999 N
Tegangan Tali 2: -384.2474354380522 N
Tegangan Tali 3: -589.7751334630568 N
Soal 2
F = 100
m = 10
g = 9.81
mu = 0.1
Cd = 0.1
A = 1
Rho = 1.2
v1 = 1
t = 40
#Friction Force
Ff = m*g*mu
#Drag Force
Fd = (Cd*A*Rho*v1**2)/2
def d2ydt2(t, y):
return((m/F) - (1/(g*mu)) - ((2*m)/(Cd*Rho*A*v1**2)))
#Misal:
t0 = 0
y = 0
h = 1
def rungekutta(t0, y0, t, h):
n = (int)((t - t0)/h)
y = y0
for i in range(1, n + 1):
"Apply Runge Kutta Formulas to find next value of y"
k1 = h * d2ydt2(t0, y)
k2 = h * d2ydt2(t0 + 0.5 * h, y + 0.5 * k1)
k3 = h * d2ydt2(t0 + 0.5 * h, y + 0.5 * k2)
k4 = h * d2ydt2(t0 + h, y + k3)
# Update next value of y
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# Update next value of x
t0 = t0 + h
return y
print(rungekutta(t0, y, t, h))
Result: 4.44s
Revisi
F = 500
m = 100
g = 9.81
mu = 0.1
Cd = 0.1
A = 1
Rho = 1.2
v0 = 0
vf = 40
#Friction Force
Ff = m*g*mu
#Drag Force
Fd = (Cd*A*Rho*vf**2)/2
def dtdtv(t, v):
return((m)/(F - Ff - Fd))
#Misal:
t = 0
h = 0.01
def rungekutta(v0, t0, vf, h):
n = (int)((vf - v0)/h)
t = t0
for i in range(1, n + 1):
"Apply Runge Kutta Formulas to find next value of y"
k1 = h * dtdtv(v0, t)
k2 = h * dtdtv(v0 + 0.5 * h, t + 0.5 * k1)
k3 = h * dtdtv(v0 + 0.5 * h, t + 0.5 * k2)
k4 = h * dtdtv(v0 + h, t + k3)
# Update next value of t
t = t + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# Update next value of v
v0 = v0 + h
return t
tf = rungekutta(v0, t, vf, h)
print(tf)
Result: 13.076168682575311
Torpedo Calculation Dilakukan analisis terhadap torpedo Mark 48
from math import*
import pandas as pd
from matplotlib import pyplot as plt
#Data from Mark 48 Torpedo
Fthrust = 20000
DragCoef = 0.22
LiftCoef = 0.3
Rho = 1000
r = 0.265
A = 3.14*r**2
Afin = 0.2
m = 1558
Vol = 1.22
alphadegrees = 30
alpha = alphadegrees*3.14/180
g = 9.81
vx0 = 0
vy0 = 0
hx = 0.1
tx0 = 0
error = 100
lstx = []
def dvxdt(tx0,vx0):
return((Fthrust*cos(alpha) - 0.5*DragCoef*Rho*A*vx0**2)/m)
while error > 0.1:
k1 = hx * dvxdt(tx0,vx0)
k2 = hx * dvxdt(tx0 + 0.5 * hx, vx0 + 0.5 * k1)
k3 = hx * dvxdt(tx0 + 0.5 * hx, vx0 + 0.5 * k2)
k4 = hx * dvxdt(tx0 + hx, vx0 + k3)
vx1 = vx0 + (1.0/6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
tx0 = tx0 + hx
error = ((vx1 - vx0)/vx1)*100
vx0 = vx1
lstx.append(vx1)
tx = len(lstx)
lstx.append(vx1)
hy = 0.1
ty0 = 0
error = 100
lsty = []
def dvydt(ty0,vy0):
return((Fthrust*sin(alpha) + Rho*((Vol*g) + 0.5*LiftCoef*Afin) - m*g -
0.5*DragCoef*Rho*A*vy0**2)/m)
while error > 0.1:
g1 = hy * dvydt(ty0,vy0)
g2 = hy * dvydt(ty0 + 0.5 * hy, vy0 + 0.5 * g1)
g3 = hy * dvydt(ty0 + 0.5 * hy, vy0 + 0.5 * g2)
g4 = hy * dvydt(ty0 + hx, vy0 + k3)
vy1 = vy0 + (1.0/6.0)*(g1 + 2 * g2 + 2 * g3 + g4)
ty0 = ty0 + hy
error = ((vy1 - vy0)/vy1)*100
vy0 = vy1
lsty.append(vy1)
ty = len(lsty)
lsty.append(vy1)
print("Time required to reach max horizontal velocity: ", tx+1, "seconds")
print("Maximum Horizontal Velocity: ", vx1, "m/s")
print("Time required to reach max vertical velocity: ", ty+1, "seconds")
print("Maximum Vertical Velocity: ", vy1, "m/s")
lstxr = [round(u,2) for u in lstx]
graphx = list(range(1,tx+2))
plt.plot(graphx,lstxr)
plt.title("Horizontal Velocty Graph")
plt.ylabel("Horizontal Velocity (m/s)")
plt.xlabel("Time (seconds)")
plt.show()
lstyr = [round(i,2) for i in lsty]
graphy = list(range(1,ty+2))
plt.plot(graphy,lstyr)
plt.title("Vertical Velocity Graph")
plt.ylabel("Vertical Velocity (m/s)")
plt.xlabel("Time (seconds)")
plt.show()
Output: Time required to reach max horizontal velocity: 63 seconds Maximum Horizontal Velocity: 26.418908231173756 m/s Time required to reach max vertical velocity: 91 seconds Maximum Vertical Velocity: 16.32477384211023 m/s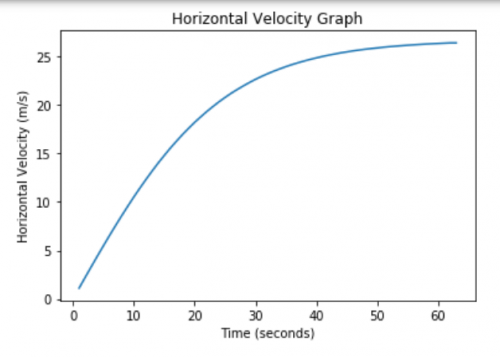


Enable comment auto-refresher