Difference between revisions of "Rafiq Ali Abdillah Azizi"
| Line 126: | Line 126: | ||
2. coding untuk penyelesaian persamaan diferensial | 2. coding untuk penyelesaian persamaan diferensial | ||
| − | + | def dydx(x, y): | |
| − | + | return ((x**2 - 4*y)) | |
| − | + | # mencari nilai y dengan nilai x tertentu pada suatu posisi tertentu h | |
| − | + | # dan nilai awal y0 pada x0 | |
| − | + | def rungeKutta(x0, y0, x, h): | |
| − | + | ||
| − | " | + | n = (int)((x - x0)/h) |
| − | + | ||
| − | + | y = y0 | |
| − | + | for i in range(1, n + 1): | |
| − | + | "menggunakan metode runge kutta untuk mencari y dan dengan terlebih dahulu mencari nilai k nya" | |
| + | "y ahir=y awal+1/6(k1+2*k2+2*k3+k4)" | ||
| + | k1 = h * dydx(x0, y) | ||
| + | k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) | ||
| + | k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) | ||
| + | k4 = h * dydx(x0 + h, y + k3) | ||
| − | + | # hasil y ahir | |
| − | + | y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | |
| − | + | # hasil x pada posisi h | |
| − | + | x0 = x0 + h | |
| − | + | return y | |
| − | + | #misalkan : | |
| − | + | x0 = 0 | |
| − | + | y = 1 | |
| − | + | x = 0.03 | |
| − | + | h = 0.01 | |
| − | + | print ('nilai y saat x adalah :', rungeKutta(x0, y, x, h)) | |
Revision as of 01:17, 17 October 2019
بسم الله الر حمن الر حيم
wong bumen njajal nulis mugo lancar
SAIKI DURUNG BISO,AKU RAK POPO SENG PENTING USAHA
Contents
Mengapa harus belajar kalkulus?
dalam suatu kehidupan sudah pasti akan ada ilmu yang mengikuti baik ilmu yang pasti maupun yang tidak pasti karena orang hidup diperintahkan untuk mencari ilmu. semakin majunya zaman sudah pasti diikut sertai kemajuan dalam hal teknologi juga. untuk membentuk suatu alat yang mencerminkan kemajuan teknologi sudah pasti dibutuhkan berbagai perhitungan baik dari perhitungan kekuatan maupun ketelitian suatu design agar tercipta suatu alat yang sesuai dengan kebutuhan dan keamanan yang terjamin. Karenanya dibutuhkan suatu perhitungan-perhitungan dasar, dari situlah kalkulus sangat dibutuhkan sebagai dasar ilmu perhitungan yang pasti. sebagai seorang engineer sudah pastinya kita harus pandai akan hal dasar INI.
MINGGU DEPAN SINAU PYTHON (BAHASA PEMOGRAMAN)
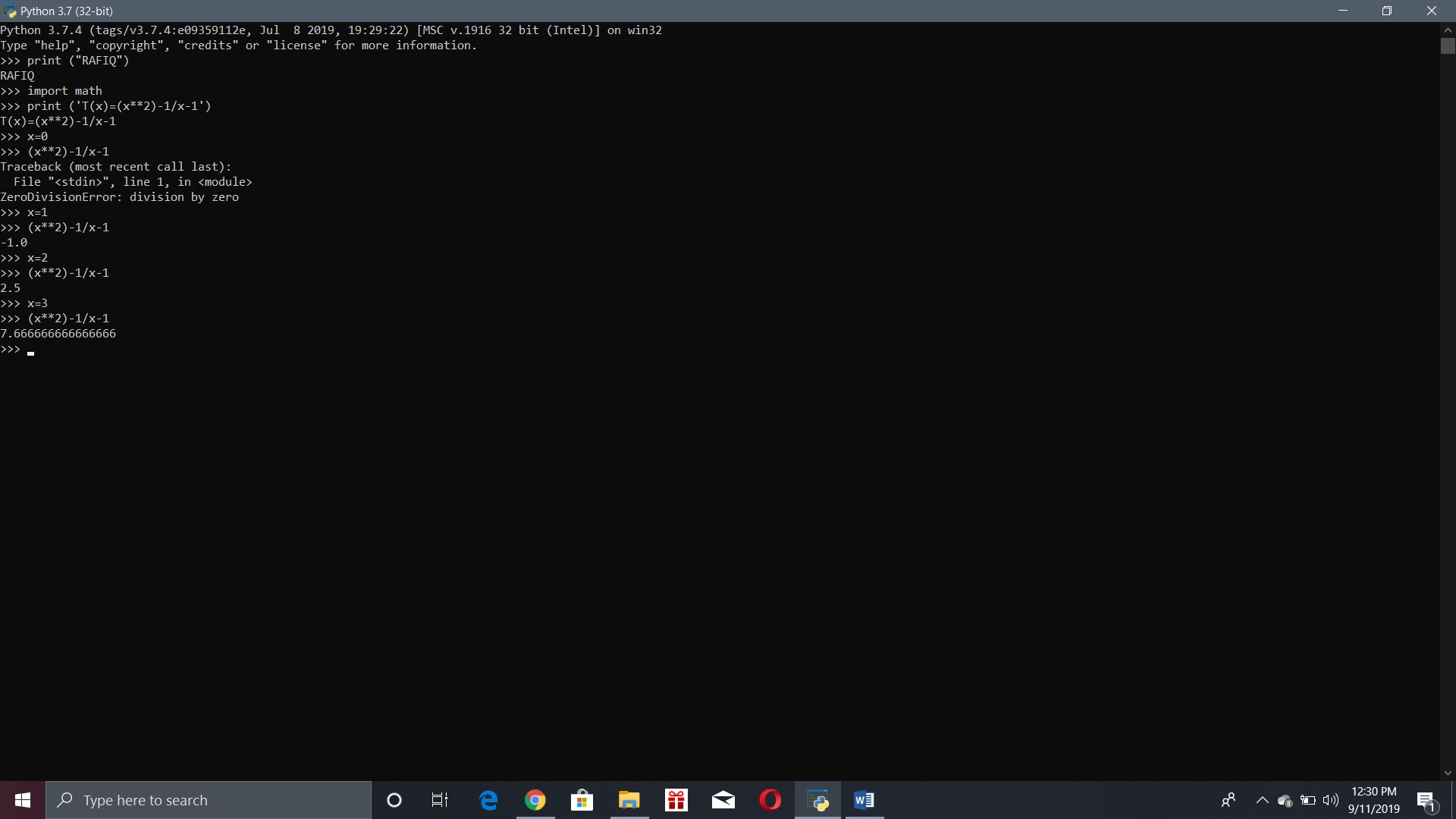
T(x)=(x^2-1)/(x-1)
Pertemuan Ke-Dua
Pertemuan Ke-Tiga
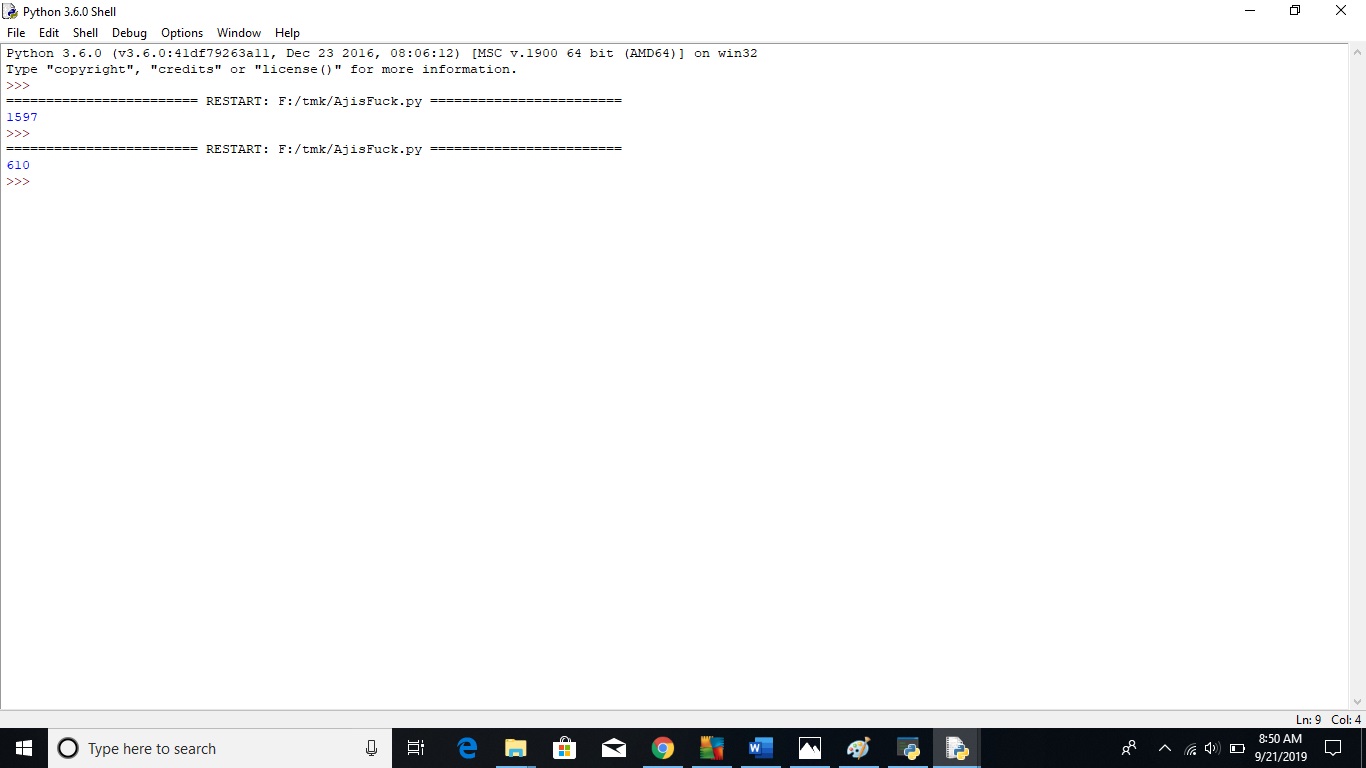
Deret Fibonaci dengan python
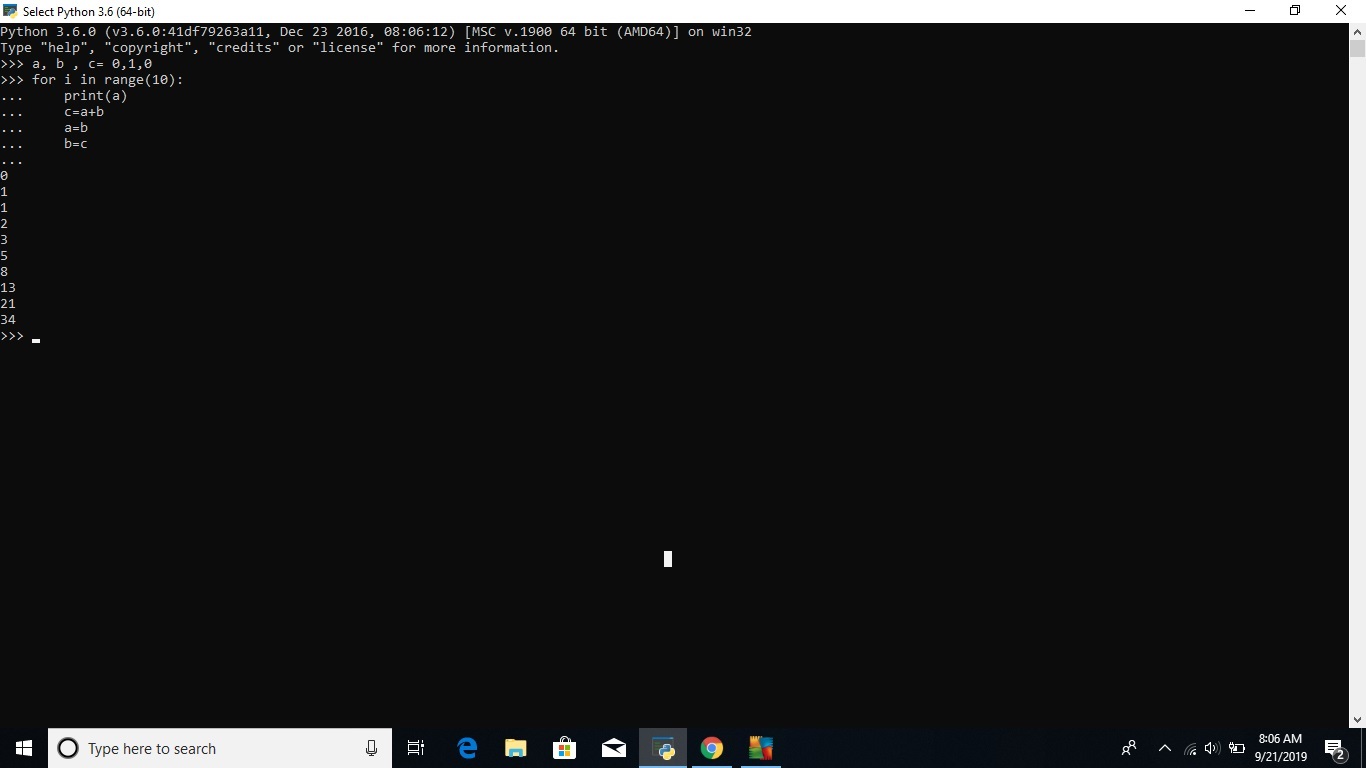
A. Jika menggunakan for
1. Mulai
2. Buatlah deret yang diingin kan, misal dengan variabel "a,b,c = 0,1,0" a dengan nilai 0 karena deret diminta dari 0
3. lalu "for in range (10)" itu untuk mengatur berapa jumlah suku yg diinginkan, jika (10) maka jumlah sukunya ada 10
4. "print(a)" untuk membuat deret sesuai dengan perintah suku pertama a dan diatas a yang diminta adalah 0
5. masukkan rumus umum fibonaci dengan variabel a,b,c "c=a+b , a=b , b=c"
6. selesai
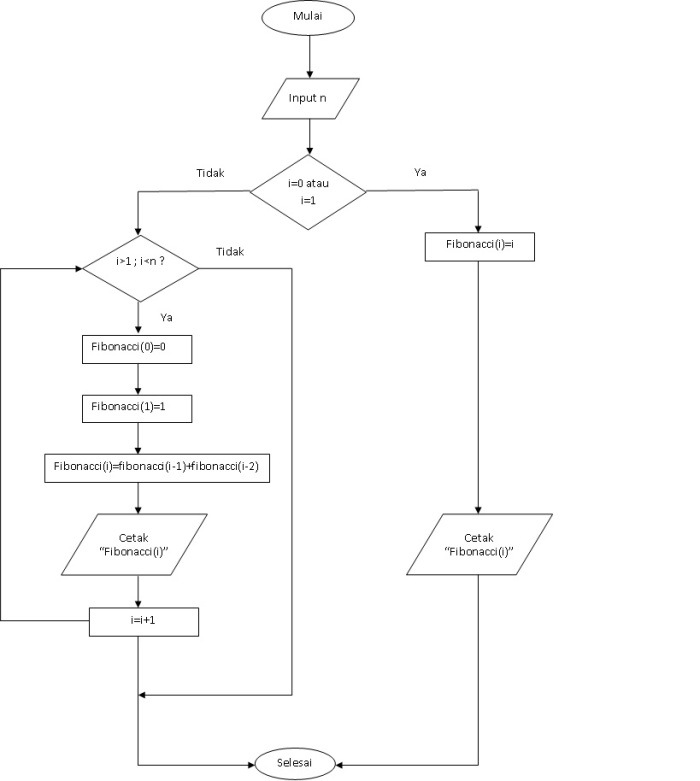
B. Dengan Function
1. Mulai
2. Masukkan n, yaitu banyaknya bilangan fibonacci yang diinginkan
3. Tentukan nilai i untuk suku pertama dan kedua yaitu i=0 atau i=1
4. Jika i=0 atau i=1 cetak fibonacci(i)=i
5. Isi nilai i>1 dimana i≤n
6. Tambahkan nilai pada variabel fibonacci di bilangan ke (i-1) dengan nilai pada variabel fibonacci di bilangan ke (i-2) kemudian nyatakan ke variabel fibonacci pada indeks ke i.
8. Cetak nilai variabel fibonacci(i)
9. Tambahkan i dengan 1
10. Selesai
Coding Kuis Aljabar dan persamaan diferensial
1. Persamaan Aljabar simultan dengan A.X = B
from numpy import linalg
import numpy as np
matAbar1 = [0,0,2,1,2]
matAbar2 = [0,1,0,2,-1]
matAbar3 = [1,2,0,-2,1]
matAbar4 = [0,0,0,-1,1]
matAbar5 = [0,1,-1,1,-1]
A = np.array ([matAbar1,matAbar2,matAbar3,matAbar4,matAbar5])
print ("matriks yang diketahui:")
print (A)
B = np.array ([1,1,-4,-2,-1])
print ("matriks hasil kali matriks yang diketahui dengan x:")
print (B)
jawab = linalg.solve (A,B)
matXkol1 = int(jawab[0])
matXkol2 = int(jawab[1])
matXkol3 = int(jawab[2])
matXkol4 = int(jawab[3])
matXkol5 = int(jawab[4])
print ("hasil X adalah :")
print ("matXkol1= ",matXkol1)
print ("matXkol2= ",matXkol2)
print ("matXkol3= ",matXkol3)
print ("matXkol4= ",matXkol4)
print ("matXkol5= ",matXkol5)
2. coding untuk penyelesaian persamaan diferensial
def dydx(x, y):
return ((x**2 - 4*y))
- mencari nilai y dengan nilai x tertentu pada suatu posisi tertentu h
- dan nilai awal y0 pada x0
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
"menggunakan metode runge kutta untuk mencari y dan dengan terlebih dahulu mencari nilai k nya"
"y ahir=y awal+1/6(k1+2*k2+2*k3+k4)"
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# hasil y ahir
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# hasil x pada posisi h
x0 = x0 + h
return y
- misalkan :
x0 = 0 y = 1 x = 0.03 h = 0.01 print ('nilai y saat x adalah :', rungeKutta(x0, y, x, h))