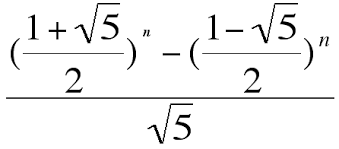Difference between revisions of "Farhan Tiarrafi Pratama"
| Line 177: | Line 177: | ||
- Numpy | - Numpy | ||
- Sympy | - Sympy | ||
| + | |||
| + | |||
| + | == Jawaban Quiz : 17 Oktober 2019 == | ||
| + | |||
| + | Pada Hari Rabu, 17 Oktober 2019 diadakan quiz untu mengerjakan soal, berikut soalnya dapat dilihat dari buku "Numerical Method for engineers python 3" pada halaman : | ||
| + | |||
| + | 1. Hal 55 Pada Lathian 2.1 soal nomor 6 | ||
| + | |||
| + | 2. Hal 263 Pada Lathihan 7.1 soal nomor 6 | ||
| + | |||
| + | |||
| + | perintah yang diberikan untuk dikerjakan pada AIR (Ahmad Indra Research) adalah bahasa pemograman python pada soal soal tersebut. | ||
| + | |||
| + | |||
| + | '''Berikut Jawabannya''' | ||
| + | |||
| + | '''Jawaban Soal pertama menggunakan metode 1''' | ||
| + | |||
| + | #Mendefinisikan matriks A | ||
| + | Ba1 = [0, 0, 2, 1, 2] | ||
| + | Ba2 = [0, 1, 0, 2, -1] | ||
| + | Ba3 = [1, 2, 0, -2, 0] | ||
| + | Ba4 = [0, 0, 0, -1, 1] | ||
| + | ba5 = [0, 1, -1, 1, -1] | ||
| + | |||
| + | nmat = np.array ([Ba1, Ba2, Ba3, Ba4, Ba5]) | ||
| + | |||
| + | #mendefinisikan matriks B | ||
| + | B = np.array ([1, 1, -4, -2, -1]) | ||
| + | |||
| + | #Dibawah ini adalah kode untuk memecahkan persamaan aljabar linear bertuliskan (linalg) | ||
| + | jawaban = linalg.solve (nmat,B) a = int(jawaban[0]) b = int(jawaban[1]) c = int(jawaban[2]) d = int(jawaban[3]) f = int(jawaban[4]) | ||
| + | |||
| + | #memunculkan hasil | ||
| + | print("X1 adalah ", a) print("X2 adalah ", b) print("X3 adalah ", c) print("X4 adalah ", d) print("X5 adalah ", f) | ||
| + | |||
| + | #maka dari cara kedua didapat matriks Xnya adalah | ||
| + | X1 adalah 2 | ||
| + | |||
| + | X2 adalah -2 | ||
| + | |||
| + | X3 adalah 1 | ||
| + | |||
| + | X4 adalah 1 | ||
| + | |||
| + | X5 adalah -1 | ||
| + | |||
| + | |||
| + | '''Jawaban Soal pertama menggunakan metode 2''' | ||
| + | |||
| + | #mendefinisikan Matriks A | ||
| + | A = np.array([[0, 0, 2, 1, 2], | ||
| + | [0, 1, 0, 2, -1], | ||
| + | [1, 2, 0, -2, 0], | ||
| + | [0, 0, 0, -1, 1], | ||
| + | [0, 1, -1, 1, -1]], float) | ||
| + | |||
| + | #Mendefinisikan Matriks B | ||
| + | b = np.array([[1], | ||
| + | [1], | ||
| + | [-4], | ||
| + | [-2], | ||
| + | [-1]],float) | ||
| + | |||
| + | Ab = np.hstack([A, b]) print (Ab, "\n") | ||
| + | n = len(b) | ||
| + | |||
| + | #Memasuki Fase Eliminasi | ||
| + | for i in range(0, n-1): | ||
| + | |||
| + | for j in range(i + 1, n): | ||
| + | lam = Ab[i,i] / Ab[j,i] | ||
| + | Ab[j] = Ab[i] - lam * Ab[j] | ||
| + | |||
| + | print ("Hasil Dari Proses Eliminasi \n", Ab, "\n") | ||
| + | |||
| + | #Memasuki Fase Substitusi | ||
| + | for i in range(n - 1, -1, -1): | ||
| + | |||
| + | Ab[i] = Ab[i] / Ab[i, i] | ||
| + | for j in range(i - 1, -1, -1): | ||
| + | b = Ab[j] | ||
| + | lam = Ab[i,i] / Ab[j,i] | ||
| + | Ab[j] = Ab[i] - lam * Ab[j] | ||
| + | print ("Hasil dari proses substitusi \n", Ab, "\n") | ||
| + | |||
| + | x = Ab[:, 5] | ||
| + | #tinggal di selesaikan dengan mencetak nilai x | ||
| + | print ("Maka didapatkan nilai x = \n", x) | ||
| + | |||
| + | '''Jawaban Soal kedua ''' | ||
| + | |||
| + | # Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment atau dapat di sebut | ||
| + | ketelitian dalam menghitung. Kita menggunakan h = 0.01. | ||
| + | x0 = 2 | ||
| + | |||
| + | y = 1 h = 0.01 x = float(input("Berikan nilai t: ")) if x>0 : | ||
| + | |||
| + | # dydx menyatakan persamaan awal dalam soal. | ||
| + | # setelah melalui proses Didapat hasil x^2-4y | ||
| + | |||
| + | def dydx(x, y): | ||
| + | return (x**2-4*y) | ||
| + | # Memasuki implementasi perhitungan menggunakan metode Runge-Kutta. | ||
| + | def rungeKutta(x0, y0, x, h): | ||
| + | n = (int)((x - x0)/h) | ||
| + | y = y0 | ||
| + | for i in range(1, n + 1): | ||
| + | k1 = h * dydx(x0, y) | ||
| + | k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) | ||
| + | k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) | ||
| + | k4 = h * dydx(x0 + h, y + k3) | ||
| + | |||
| + | # untuk y selanjutnya | ||
| + | y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | |||
| + | # untuk x selanjutnya | ||
| + | x0 = x0 + h | ||
| + | list.append(y) | ||
| + | return y | ||
| + | print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h)) | ||
| + | |||
| + | kemudian akan didapatkan hasil apabila t=0.03 | ||
| + | |||
| + | Masukkan nilai t: 0.03 | ||
| + | |||
| + | Nilai y pada t = 0.03 adalah 1 | ||
Revision as of 01:01, 17 October 2019
Nama : Farhan Tiarrafi Pratama
NPM : 1806201075
Jurusan : Teknik Mesin
Contents
[hide]lecture 1 : 04 September 2019
1. Kenapa amak mesin belajar kalkulus ? karena pada kalkulus terdapat materi materi dasar yang dapat di pergunakan untuk melewati mata kuliah lain yang membutuhkan materi dasar tersebut. kalkulus juga berperan penting pada pembentukan pola pikir "analisis" yang dapat sangat berguna untuk seorang engineer seperti teknik mesin.
PYTHON merupakan sebuah media progamming yang digunakan untuk meminimalisir kesalahan hitungan dengan bantuan sebuah komputer. pada programming hanya dapat dilakukan pengerjaan matematika berupa pertambahan (+), pengurangan (-), perkalian(x), dan pembagian (:)
PAY ATTENTION : Penilaian secara terus menerus, perkembangan cara menguasai pemograman phyton
HOMEWORK 1. mempelajari PHYTON untuk minggu ini dengan belajar membuat sebuah program 2. membuat sebuah program agar dapat menjawab sebuah soal pada papan tulis
Tempat Belajar 1. sololearn.com
My Progres
What is phyton ? Python is a high-level programming language, with applications in numerous areas, including web programming, scripting, scientific computing, and artificial intelligence. Python has several different implementations, written in various languages. CPython, is the most popular by far.
My First Try to use phyton
1. print('Hello World') 2. print(2*4) >> 8 3. print((4+9)*5) >> 65 4. print((5+7)/2) >> 6
pada python operasi pertambahan menggunakan (+), pengurangan menggunakan (-), perkalian (*), pembagian (/), exponensial (**) error bisa terjadi pada python, contohnya ZeroDivisionErorr (Dividing by zero in Python produces an error, as no answer can be calculated)
there are 2 types of number
integer and float, integer dapat dikatakan sebagai bilangan bulat (1,2,3,4 dll) dan float merupakan bilangan yang mempunyai koma ( 2.0,3.2,4,3 dll).
ada pengoprasian khusus pada python yang dapat dikatakan floor division(//) and modulo(%) berikut contohnya:
1. print (20 // 6) >> 3 2. print (1.25 % 0.5) >> 0.25
strings : A string is created by entering text between two single or double quotation marks. When the Python console displays a string, it generally uses single quotes. The delimiter used for a string doesn't affect how it behaves in any way.
Variables: Variables play a very important role in most programming languages, and Python is no exception. A variable allows you to store a value by assigning it to a name, which can be used to refer to the value later in the program. to assign a variable, use one equals sign. Unlike most lines of code we've looked at so far, it doesn't produce any output at the Python console. for example :
x = 7 print(x) 7 print(x + 3) 10 print(x) 7
x = 123.456 print(x) 123.456 x = "This is a string" print(x + "!") This is a string!
foo= input("99")
print(foo)
99
Tugas ( 4 sept 2019 )
Lecture 2 : 11 September 2019
rec=('Farhan','Tiarrafi','Pratama',(28,6,2001))
NamaAwal,NamaTengah,NamaAkhir,TanggalLahir=rec
print(NamaAwal)
TahunLahir = TanggalLahir [2]
print(TahunLahir)
name = rec[0]++rec[1]
print(name)
print(rec[0:3])
Farhan
2001
FarhanTiarrafi
('Farhan', 'Tiarrafi', 'Pratama')
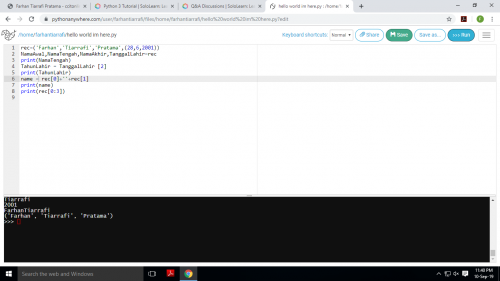
Padahari rabu 11 september 2019, diajarkan untuk membuat suatu perumpamaan dan membuat perintah untuk memanggil variable tersebut. terlihat pada foto ke (2) yang berisi perumpamaan dan perintah yang langsung dpt di lihat pada output nya.
Perbedaan 32-bit dengan 64 bit ? filosofi yang berujung bahwa hati yang melakukan pemikiran dan otak yang melakukan perhitungan atau melaksanakan. industri 5.0 adalah pancasila ?, ya itu sebuah cetusan yang dibuat pak dai. beliau menyatkan Technology must empower human. mesin merupakan numerik, numerik merupakan pelajaran ini. sebaiknya hal itu menjadi driving force untuk tetap semangat dalam mempelajari ini. pada pelajaran ini ditekankan untuk menjadikan diri manusia sebagai sebuah penggagas atau pemikir dan komputer/perangkat lunak menjadi tools yang berguna untuk mempermudah pekerjaan manusia.
Tugas Pertemuan Kedua
Pelajari buku Python Bab 1
Lecture 3 : 19 September 2019
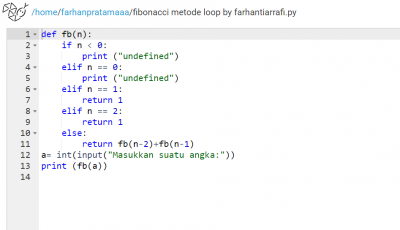
Pada pertemuan ke-tiga diadakan sebuah quiz yang bertujuan untuk melatih logika berfikir. Quiz yang di berikan berupa pemograman pada deret fibonacci.
yang ditanyakan adalah algoritma dan flowchart untuk membuat pemograman deret fibonacci, akan tetapi banyak yang belum mengetahui cara membuat program deret tersebut, hampir 1 kelas belum ada yang dapat mengerjakan. Setlah mendapat menjelasan oleh pak radon tentang pembuatan deret dan sumber dr internet juga, deret fibonacci dapat di selesaikan dengan 2 cara, yaitu :
1. Cara Loop 2. Cara function
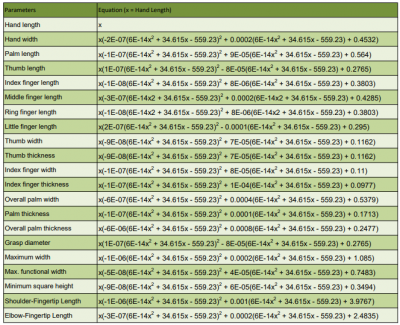
Cara loop mudah digunakan karena tidak perlu menemukan pola yang amat rumit, karena jika memakai function kita harus menemukan sebuah fungsi untuk di input kedalam pemograman yang dimana fungsi itu sangat sulit di dapatkan. berikut merupakan formula dr deret fibonacci :
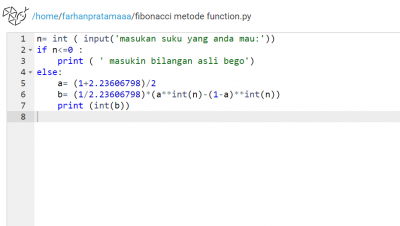
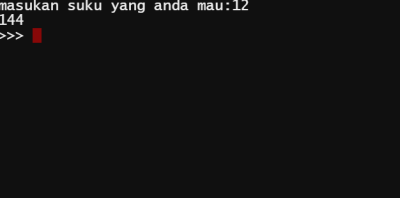
setlah mendapat penjelasan kita kembali membuat pemograman deret fibonacci menggunakan 2 metode, dengan loop dan function.
1. Cara Loop
2. cara function
Lecture 4 : 25 September 2019
Pada hari ini mempelajari permodelan komputer. Karena dalam mempelajari suatu konsep harus mengerti sangat akan konsep tersebut. oleh karena itu hari ini disampaikan isi dari permodelan komputer itu sendiri.
sebelum sampai ke ranah sana, ada sebuah pertanyaan, mengapa sebagai anak teknik kita harus berhitung ?
karena apa yang kita buat, apa yang kita design akan kita pertanggung jawabkan fungsional nya. Semua barang/alat yang kita buat akan mempunyai spesifikasi dan perhitungan yang berbeda. Namun manusia tetap manusia, mempunyai batas. Manusia hanya bisa melakukan usaha pendekatan akan suatu jawaban.
selanjutnya kita masuk ke bahasa kita, Apa itu model ?
model merupakan simplifikasi/penyederhanaan dari sebuah kasus/keadaan yang rumit.
model terdiri dari 3 Unsur, yaitu : 1. Asumsi 2. Simplifikasi 3. Representasi
Contoh dari sebuah model pada fondasi. Untuk menghitung kekuatan fondasi menahan beban. Fondasi di modelkan dalam bentuk 2D dan di asumsikan Modulus Elastisitas pada semua titik sama, lalu mensimplifikasi dengan menggunakan model 2D.
Dari berbagai model yang kita buat, dibutuhkan ilmu dalam membangun persamaan aljabar dan memodelkan persamaan dalam komputasi. Untuk itu kita harus belajar giat serta berlatih sejak dini untuk menggunakan komputasi. Selain itu ada juga aplikasi dari komputasi yaitu Diskritisasi yaitu membuat sesuatu yang kontinu menjadi titik-titik yang berhingga.
Lecture 5 : 2 Oktober 2019
Hampir Semua masalah yang ada di dunia dapat di buat menjadi sebuah model. salah satu ialah menggunakan bahasa python sebagai penyelesaian masalah. mengapa python ? dikarenakan python gratis di sebar kepada khalayak luas dan sangat mendukung dalam industri 4.0 pada hari ii mempelajari : 1. aplikasi al jabar yang akan di modelkan pada sistem pegas 2. mempelajari bagaimana membuat rangkaian pegas dengan bahasa python
Tugas untuk minggu depan
1. Membaca Bab 7 2. Pelajari methode Runge Kutta
Pada pertemuan hari ini, Asdos menjelaskan tentang Penggunaan Pemodelan pada Sistem Tunggal menjadi sebuah persamaan linier dengan menerjemahkan rumus yang biasa digunakan pada materi Pegas menjadi sebuah matriks yang berisikan konstanta pegas. Selain itu pada pertemuan ini mempelajari tentang Cara Pembuatan Matriks Pegas yang tidak Tunggal yaitu dengan menerapkan Superposisi Matriks. Lalu, diberikan contoh pemodelan sistem ganda pada pegas seri.
Terakhir diberikan penjelasan dan cara penggunaan modul yang dapat digunakan pada Python yang dapat memudahkan perhitungan Sistem Persamaan Linier yaitu :
- Numpy - Sympy
Jawaban Quiz : 17 Oktober 2019
Pada Hari Rabu, 17 Oktober 2019 diadakan quiz untu mengerjakan soal, berikut soalnya dapat dilihat dari buku "Numerical Method for engineers python 3" pada halaman :
1. Hal 55 Pada Lathian 2.1 soal nomor 6
2. Hal 263 Pada Lathihan 7.1 soal nomor 6
perintah yang diberikan untuk dikerjakan pada AIR (Ahmad Indra Research) adalah bahasa pemograman python pada soal soal tersebut.
Berikut Jawabannya
Jawaban Soal pertama menggunakan metode 1
#Mendefinisikan matriks A Ba1 = [0, 0, 2, 1, 2] Ba2 = [0, 1, 0, 2, -1] Ba3 = [1, 2, 0, -2, 0] Ba4 = [0, 0, 0, -1, 1] ba5 = [0, 1, -1, 1, -1]
nmat = np.array ([Ba1, Ba2, Ba3, Ba4, Ba5])
#mendefinisikan matriks B B = np.array ([1, 1, -4, -2, -1])
#Dibawah ini adalah kode untuk memecahkan persamaan aljabar linear bertuliskan (linalg) jawaban = linalg.solve (nmat,B) a = int(jawaban[0]) b = int(jawaban[1]) c = int(jawaban[2]) d = int(jawaban[3]) f = int(jawaban[4])
#memunculkan hasil
print("X1 adalah ", a) print("X2 adalah ", b) print("X3 adalah ", c) print("X4 adalah ", d) print("X5 adalah ", f)
#maka dari cara kedua didapat matriks Xnya adalah X1 adalah 2
X2 adalah -2
X3 adalah 1
X4 adalah 1
X5 adalah -1
Jawaban Soal pertama menggunakan metode 2
#mendefinisikan Matriks A
A = np.array([[0, 0, 2, 1, 2],
[0, 1, 0, 2, -1],
[1, 2, 0, -2, 0],
[0, 0, 0, -1, 1],
[0, 1, -1, 1, -1]], float)
#Mendefinisikan Matriks B
b = np.array([[1],
[1],
[-4],
[-2],
[-1]],float)
Ab = np.hstack([A, b]) print (Ab, "\n")
n = len(b)
#Memasuki Fase Eliminasi for i in range(0, n-1):
for j in range(i + 1, n):
lam = Ab[i,i] / Ab[j,i]
Ab[j] = Ab[i] - lam * Ab[j]
print ("Hasil Dari Proses Eliminasi \n", Ab, "\n")
#Memasuki Fase Substitusi for i in range(n - 1, -1, -1):
Ab[i] = Ab[i] / Ab[i, i]
for j in range(i - 1, -1, -1):
b = Ab[j]
lam = Ab[i,i] / Ab[j,i]
Ab[j] = Ab[i] - lam * Ab[j]
print ("Hasil dari proses substitusi \n", Ab, "\n")
x = Ab[:, 5]
#tinggal di selesaikan dengan mencetak nilai x
print ("Maka didapatkan nilai x = \n", x)
Jawaban Soal kedua
# Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment atau dapat di sebut ketelitian dalam menghitung. Kita menggunakan h = 0.01. x0 = 2
y = 1 h = 0.01 x = float(input("Berikan nilai t: ")) if x>0 :
# dydx menyatakan persamaan awal dalam soal. # setelah melalui proses Didapat hasil x^2-4y
def dydx(x, y):
return (x**2-4*y)
# Memasuki implementasi perhitungan menggunakan metode Runge-Kutta.
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# untuk y selanjutnya
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# untuk x selanjutnya
x0 = x0 + h
list.append(y)
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
kemudian akan didapatkan hasil apabila t=0.03
Masukkan nilai t: 0.03
Nilai y pada t = 0.03 adalah 1