Difference between revisions of "Kelompok 6"
(→Video Tugas Ke-empat) |
|||
| Line 5: | Line 5: | ||
1. Geofany Rosady (1706986366) | 1. Geofany Rosady (1706986366) | ||
| + | [[File:Geo.jpg|150px|thumb|right]] | ||
| + | |||
2. Jonathan Surya (1706036210) | 2. Jonathan Surya (1706036210) | ||
| Line 10: | Line 12: | ||
3. Ronald Galvin (1806200910) | 3. Ronald Galvin (1806200910) | ||
| + | __TOC__ | ||
== Pendahuluan == | == Pendahuluan == | ||
| Line 57: | Line 60: | ||
berikut gambaran soalnya | berikut gambaran soalnya | ||
| − | + | [[File:T04_6.png|500px|thumb|center]] | |
| Line 64: | Line 67: | ||
berikut contoh penyelesaian manualnya | berikut contoh penyelesaian manualnya | ||
| + | [[File:T042.jpg|500px|thumb|center]] | ||
| Line 69: | Line 73: | ||
berikut penyelesaian Pythonnya | berikut penyelesaian Pythonnya | ||
| − | + | [[File:T04_1_6.mp4|800px|thumb|center]] | |
Revision as of 12:38, 2 October 2019
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Perkenalkan kami dari kelompok 6 kelas Metode Numerik Kelas Reguler-2
Anggota dari kelompok 6 :
1. Geofany Rosady (1706986366)
2. Jonathan Surya (1706036210)
3. Ronald Galvin (1806200910)
Pendahuluan
Eliminasi Gauss-Jordan adalah integrasi dari eliminasi Gauss yang hasilnya lebih sederhana lagi. Metodenya adalah dengan meneruskan operasi baris dari eliminasi Gauss sampai menghasilkan matriks yang Eselon-baris. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Pada akhirnya ada segitiga atas/ segitiga bawah seperti:
Metode ini digunakan untuk mencari invers dari sebuah matriks. Prosedur umum untuk metode eliminasi Gauss-Jordan ini adalah 1. Ubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi. 2. Lakukan operasi baris elementer pada matriks augmentasi (A|b) untuk mengubah matriks.
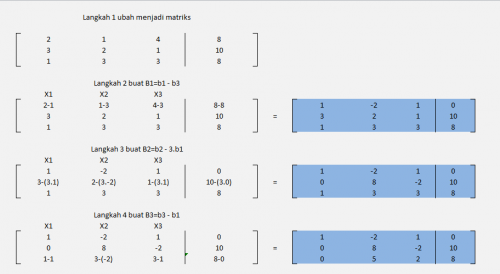
Misalkan saja: 2X1 + X2 + 4X3 = 8 3X1 + 2X2 + X3 = 10 X1 + 3X2 + 3X3 = 8
Berikut adalah penyelesaian secara matematis :
Video Tugas Ketiga
Video diatas merupakan penjelasan penggunaaan aplikasi metode numerik pada eliminasi Gauss. Algortima dari video diatas akan kami tampilkan dibawah ini:
Lalu hasil run sebagai berikut:
Terima Kasih telah membaca blog Wiki kami, jika ingin memberikan pendapat silahkan berkomentar di bawah
Video Tugas Ke-empat
Tugas keempat adalah mengaplikasikan eliminasi gauss jordan pada penyelesaian soal statistika struktur pada satu dimensi.Salah satu pengaplikasiannya kami mengambil satu contoh yaitu beam yang memiliki 2 tumpuan fix.
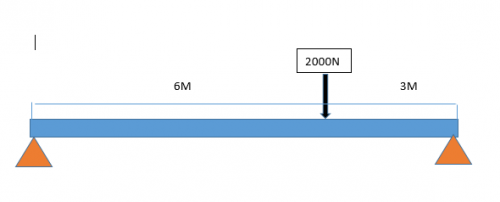
Panjang total beam L = 9m, Panjang dari A - gaya = 6m ,Panjang dari B - gaya = 3m, Gaya yang diberikan = 2000N
berikut gambaran soalnya
berikut contoh penyelesaian manualnya
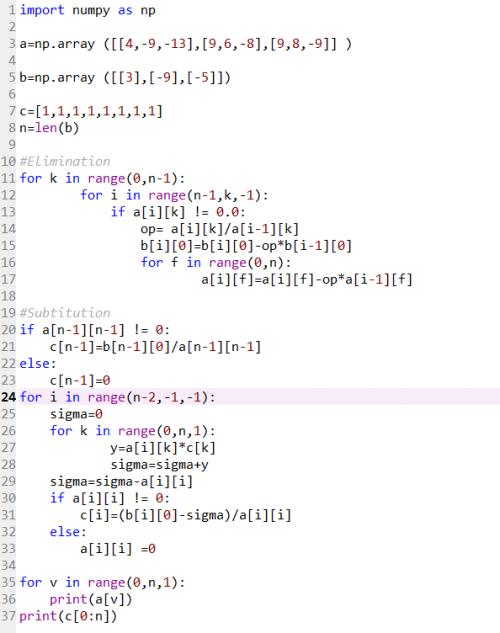
berikut penyelesaian Pythonnya
Video diatas merupakan contoh penyelesaian soal statistika struktur dengan eliminasi gauss jordan





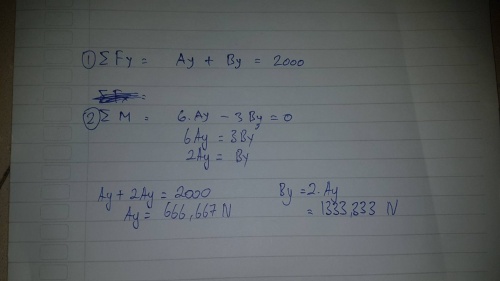
Enable comment auto-refresher
Jonathan.Surya
Permalink |
Geofany.rosady
Permalink |