Difference between revisions of "Bagus Fadhlurrohman"
(→Metode Numerik) |
(→Metode Numerik) |
||
| Line 123: | Line 123: | ||
[[Hiburan 3]] | [[Hiburan 3]] | ||
| + | |||
| + | Mencari nilai x pada | ||
| + | |||
| + | [[File:hiburan 3.jpg]] | ||
| + | |||
| + | step 1 | ||
| + | |||
| + | Tentukan persamaan pada gambar tersebut | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | 6x<sub>1</sub> + 4x<sub>2</sub> = 50 | ||
| + | 2x<sub>1</sub> + x<sub>3</sub> + 4x<sub>4</sub> = 50 | ||
| + | 7x<sub>2</sub> + 3x<sub>3</sub> + 4x<sub>4</sub> = 50 | ||
| + | 4x<sub>1</sub> + 4x<sub>3</sub> = 50 | ||
| + | |||
| + | Akan menghasilkan matriks | ||
| + | [[6. 4. 0. 0.] | ||
| + | [2. 0. 1. 4.] | ||
| + | [0. 7. 3. 4.] | ||
| + | [4. 0. 4. 0.]] | ||
| + | </div> | ||
| + | |||
| + | step 2 | ||
| + | |||
| + | tuliskan matriks di python seperti berikut | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | import numpy as np | ||
| + | <br>A = np.array([[6, 4, 0, 0], [2, 0 ,1, 4], [0, 7, 3, 4], [ 4, 0, 4, 0]], float) | ||
| + | B = np.array([50, 50, 0, 0], float) | ||
| + | <br>n = len(A) | ||
| + | </div> | ||
| + | |||
| + | dengan eliminasi gauss | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | for k in range(0,n-1): | ||
| + | for i in range(k+1,n): | ||
| + | if A[i,k]!=0 : | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam) | ||
| + | B[i] = B[i]-(B[k]*lam) | ||
| + | x = np.zeros(n,float) | ||
| + | for m in range(n-1,-1,-1): | ||
| + | x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m] | ||
| + | </div> | ||
| + | |||
| + | '''Results''' | ||
==''' Tugas Mekanika Fluida''' == | ==''' Tugas Mekanika Fluida''' == | ||
Revision as of 11:46, 29 September 2019
Profil
Nama: Bagus Fadhlurrohman
NPM: 1706070633
Fakultas: Teknik
Jurusan: Teknik Mesin
BIOGRAFI
Nama saya Bagus Fadhlurrohman lahir pada tanggal 15 Juli 1999 di kota Jakarta. Saya merupakan anak pertama dari 2 bersaudara. Ayah saya seorang karyawan dan ibu saya seorang ibu rumah tangga. Saya memiliki 1 adik laki-laki yang sudah menjadi mahasiswa.
Riwayat pendidikan
2003-2005 TK Aisiyah 04 Tebet Timur
2005-2011 SDN Tebet Barat 05 Pagi
2011-2014 SMPN 115 Jakarta
2014-2017 SMAN 8 Jakarta
2017-.... S1 Teknik Mesin Universitas Indonesia
Metode Numerik
Mencari limit (x)=1 pada persamaan dengan pyhton
(x**2-1) / ((x-1)
step 1
Membuka python idle lulu mengetik program seperti berikut
def limit (x) :
try:
a = (x**2-1)
b = (x-1)
result = a / b
print (result)
except ZeroDivisionError:
c = ((x+(1/99))**2-1) / ((x+(1/99))-1)
print (c)
d = ((x+(1/999))**2-1) / ((x+(1/999))-1)
print (d)
e = ((x+(1/9999))**2-1) / ((x+(1/9999))-1)
print (e)
f = ((x+(1/99999))**2-1) / ((x+(1/99999))-1)
print (f)
g = ((x+(1/999999))**2-1) / ((x+(1/999999))-1)
print (g)
h = ((x+(1/9999999))**2-1) / ((x+(1/9999999))-1)
print (h)
print ("mendekati angka 2")
else:
print ("hasilnya", resut)
finally:
print ("sudah")
step 2
simpan program dalam bentik file.py
step 3
jalankan program pada python
step 4
nanti akan mendapatkan hasil File:Hiburan 1.jpg
Mencari nilai x pada persamaan dengan python
8x**4 + 2x**3 + x**2 - x = 0
step 1
Membuka python idle lulu mengetik program seperti berikut
def f(x):
return 8*x**3 + 2*x**2 + x - 1
def fprime(x):
return 24*x**2 + 4*x +1
ep = 0.001
gu = -10 i = 0
print('8*x**3 + 2*x**2 + x - 1')
print('Results by Python 3.7')
while abs(f(gu)) >= ep:
gu = gu - (f(gu)/fprime(gu))
i += 1
print(' ' + str(i) + ' ' + str(round(gu,7)))
print('The root approach is ' + str(round(gu,2)) +
'| failed to calculate: ' + str(i) + ' times' )
step 2
simpan program dalam bentik file.py
step 3
jalankan program pada python
step 4
nanti akan mendapatkan hasil File:Hiburan 2.jpg
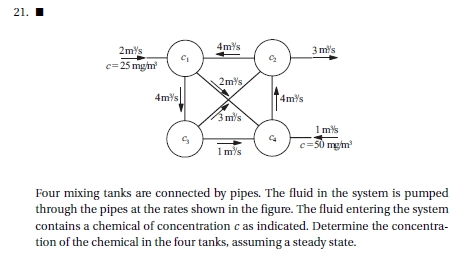
Mencari nilai x pada
step 1
Tentukan persamaan pada gambar tersebut
6x1 + 4x2 = 50 2x1 + x3 + 4x4 = 50 7x2 + 3x3 + 4x4 = 50 4x1 + 4x3 = 50
Akan menghasilkan matriks [[6. 4. 0. 0.]
[2. 0. 1. 4.] [0. 7. 3. 4.] [4. 0. 4. 0.]]
step 2
tuliskan matriks di python seperti berikut
import numpy as np
A = np.array([[6, 4, 0, 0], [2, 0 ,1, 4], [0, 7, 3, 4], [ 4, 0, 4, 0]], float) B = np.array([50, 50, 0, 0], float)
n = len(A)
dengan eliminasi gauss
for k in range(0,n-1):
for i in range(k+1,n):
if A[i,k]!=0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
B[i] = B[i]-(B[k]*lam)
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]
Results