Difference between revisions of "Stefanus Nandiwardhana Mahardhika"
| Line 31: | Line 31: | ||
---- | ---- | ||
| − | Pemecahan soal limit (x^2 - 1)/(x - 1) ternyata tidaklah gampang. Awalnya saya mencoba-coba berusaha membuat koding sendiri dari awal tanpa bantuan library. Namun, setelah mencoba-coba dan gagal, akhirnya saya memutuskan untuk menggunakan bantuan ''Sympy Library''. Berikut hasilnya: | + | 1. Pemecahan soal limit (x^2 - 1)/(x - 1) ternyata tidaklah gampang. Awalnya saya mencoba-coba berusaha membuat koding sendiri dari awal tanpa bantuan library. Namun, setelah mencoba-coba dan gagal, akhirnya saya memutuskan untuk menggunakan bantuan ''Sympy Library''. Berikut hasilnya: |
[[File:HW_1 Stefanus.jpg]] | [[File:HW_1 Stefanus.jpg]] | ||
| Line 45: | Line 45: | ||
Jawaban yang didapatkan adalah 2. | Jawaban yang didapatkan adalah 2. | ||
| + | |||
| + | |||
| + | 2. Aplikasi dari metode numerik tentunya sangat banyak, mengingat metode numerik adalah salah satu cara pemecahan permasalahan perhitungan matematika dengan solusi yang berupa perkiraan sehingga penyelesaiannya cenderung lebih sederhana daripada metode analitik. Berikut adalah contoh aplikasi dari metode numerik: | ||
| + | *Penyelesaian persamaan diferensial | ||
| + | *Regresi | ||
| + | *Interpolasi | ||
| + | *Integrasi Numerik | ||
| + | *Differensiasi Numerik | ||
| + | Semuanya tentunya sangat dibutuhkan dalam banyak bidang, terutama bidang ke-teknik-an. | ||
Revision as of 03:18, 9 September 2019
Introduksi
Perkenalkan, nama saya Stefanus Nandiwardhana Mahardhika (Akrab dipanggil Evan). Saya adalah mahasiswa Teknik Mesin di Universitas Indonesia angkatan 2017. Saya adalah salah satu dari sekian banyak mahasiswa rantau di Universitas Indonesia. Saya lahir di Kota Yogyakarta pada tanggal 25 Februari 1999.
Nama: Stefanus Nandiwardhana Mahardhika Jurusan: Teknik Mesin Angkatan: 2017 NPM: 1706036160
Kenapa Anak Teknik Mesin Harus Belajar Kalkulus?
Menurut saya kalkulus adalah salah satu ilmu yang mendasar dalam ilmu ke-Teknik-an. Tidak jarang dalam memecahkan sebuah masalah, baik yang kompleks maupun yang sederhana, kita sebagai orang teknik memerlukan ilmu kalkulus. Dari memplot grafik sampai menghitung efisiensi sebuah pembangkit listrik tenaga uap, terdapat banyak hal yang tidak bisa terlepas dari penggunaan ilmu kalkulus.
Pertemuan Pertama
Pada pertemuan pertama mata kuliah metode numerik ini, saya dikenalkan dengan Dr. Ahmad Indra dan Dr. Eng. Radon Dhelika. Kuliah diawali dengan penjelasan singkat akan mata kuliah Metode Numerik oleh Pak Dai. Beliau juga menjelaskan akan sistem penilaian di kelas ini yang lebih melihat kepada perkembangan yang dialami oleh mahasiswa selama mengikuti mata kuliah ini. Hal ini dikarenakan kepercayaan Pak Dai dan Pak Radon terhadap continuous learning. Pak Radon kemudian menambahkan alasan penggunaan bahasa koding Python dalam pembelajaran mata kuliah ini yang berupa semakin populernya penggunaan bahasa Python dalam berbagai hal. Hal ini memudahkan mahasiswa dalam mencari informasi bantuan dalam mempelajarinya.
Tugas 2: *Pelajari Python *Buatlah sebuah program untuk memecahkan soal limit (x^2 - 1)/(x - 1) dengan algoritma flowchart/kata-kata. *Tulis aplikasi dari metode numerik
Tugas 1
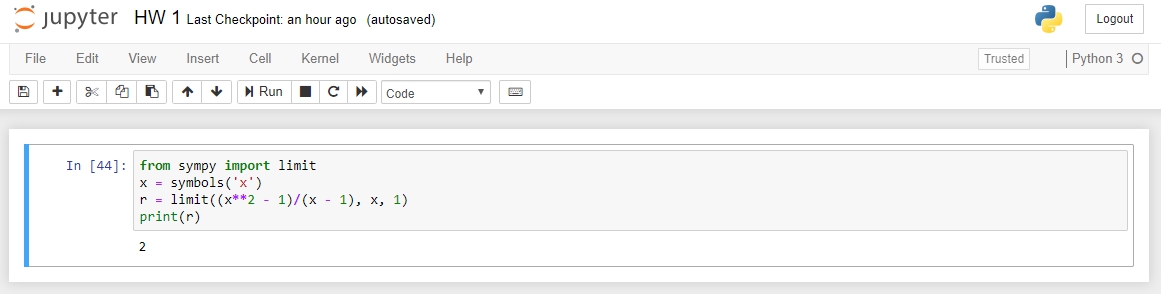
1. Pemecahan soal limit (x^2 - 1)/(x - 1) ternyata tidaklah gampang. Awalnya saya mencoba-coba berusaha membuat koding sendiri dari awal tanpa bantuan library. Namun, setelah mencoba-coba dan gagal, akhirnya saya memutuskan untuk menggunakan bantuan Sympy Library. Berikut hasilnya:
Penggunaan Sympy Library sangatlah mempersingkat dan menyederhanakan koding yang perlu ditulis.
Saya menggunakan Jupyter Notebook sebagai interface editor dalam menulis koding Python dengan bantuan Anaconda Navigator sebagai launcher-nya.
Line 1: Koding yang saya tulis diawali dengan "from sympy import limit" untuk melakukan impor modul simpy yang berhubungan dengan limit. Saya juga bisa menggunakan "*" untuk menggantikan "limit" untuk mengimpor semua modul dan membiarkannya mencari sendiri modul yang berhubungan.
Line 2: Kemudian saya menetapkan x sebagai simbol x yang ada di simpy
Line 3: Kemudian saya menetapkan sebuah karakter acak ("r") untuk ditetapkan sebagai persamaan yang ingin dicari (limit (x^2 - 1)/(x - 1)). Setelah penulisan persamaan, saya memberi tanda koma untuk menuliskan variabel dan angka yang didekati.
Line 4: Terakhir, saya memerintahkan agar jawaban dari persamaan tadi dicetak.
Jawaban yang didapatkan adalah 2.
2. Aplikasi dari metode numerik tentunya sangat banyak, mengingat metode numerik adalah salah satu cara pemecahan permasalahan perhitungan matematika dengan solusi yang berupa perkiraan sehingga penyelesaiannya cenderung lebih sederhana daripada metode analitik. Berikut adalah contoh aplikasi dari metode numerik:
- Penyelesaian persamaan diferensial
- Regresi
- Interpolasi
- Integrasi Numerik
- Differensiasi Numerik
Semuanya tentunya sangat dibutuhkan dalam banyak bidang, terutama bidang ke-teknik-an.