Difference between revisions of "Faiz Gading Rahmadana"
| Line 12: | Line 12: | ||
Pada kelas kali ini, Dosen meminta Mahasiswa mengaproksimasikan nilai dari Sin(pi/7). Menggunakan rumus umum diatas. Pola didapat yaitu -x^2/2n(2n+1). Masukkan ke dalam Microsoft Excel. Simsalabim. Jawaban pun dapat dicari serinci mungkin. Kesimpulan blog saya kali ini. Hidup ini mudah. Sebetulnya. Hanya perlu perbanyak membaca. Jadi paham bagaimana cara menggunakannya. Ilmu dasar, terutama teknologi. Because, that's why it does exist. Makes everything easier. | Pada kelas kali ini, Dosen meminta Mahasiswa mengaproksimasikan nilai dari Sin(pi/7). Menggunakan rumus umum diatas. Pola didapat yaitu -x^2/2n(2n+1). Masukkan ke dalam Microsoft Excel. Simsalabim. Jawaban pun dapat dicari serinci mungkin. Kesimpulan blog saya kali ini. Hidup ini mudah. Sebetulnya. Hanya perlu perbanyak membaca. Jadi paham bagaimana cara menggunakannya. Ilmu dasar, terutama teknologi. Because, that's why it does exist. Makes everything easier. | ||
| + | |||
| + | |||
| + | |||
| + | == '''Pertemuan 2, 10 September 2019''' == | ||
| + | Jangan sia-siakan waktu satu detik pun. Tidak ada yang tahu kapan rejeki datang. Mungkin di detik tersebut. Seperti Pandji Pragiwaksono. Saat masih menjadi penyiar Hard Rock FM Bandung. | ||
| + | Begitu tertanam pengalaman Pandji di hidup saya. Hari ini pun saya mendapat ilmu penting. '''Pseudocode'''. | ||
Revision as of 19:01, 16 September 2019
Profil
Perkenalkan, saya Faiz Gading Rahmadana. Kalian bisa panggil saya Faiz. Jurusan Teknik Mesin. Sekarang tahun ketiga saya. NPM bila kalian butuh, 1706986353. Laman ini akan dipenuhi celotehan saya. Tentu bermanfaat. Terima kasih kepada Dr. Ir. Ahmad Indra Siswantara dan Dr. Ir. Engkos Achmad Kosasih M.T. telah menyediakan tool yang menarik. Bagus untuk mulai nge-blog.
Pertemuan 1, 3 September 2019
Kelas Metode Numerik kali ini cukup menarik perhatian. Sama sekali tidak ada hal lain yang saya lakukan selain memperhatikan ilmu yang diberikan oleh para Dosen. Bagi yang awam istilah Metode Numerik (Metnum). Manusia punya batasan. Butuh bantuan menyelesaikan persoalan matematika. Untuk persoalan dasar saya yakin semuanya hebat. Apalagi Mahasiswa DTM. Dibimbing oleh Dosen-Dosen profesional. Tidak ada keraguan lagi. Nah, Metnum disini adalah teknik yang memformulasikan persoalan matematika hingga bisa dipecahkan dengan perhitungan biasa. Seperti perkalian dan pengurangan. Jadi sangat mempermudah manusia.
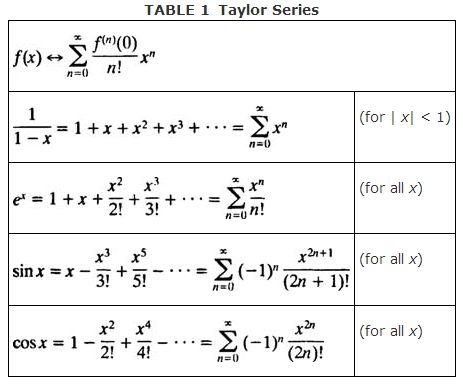
Taylor's Method itu salah satunya. Representasi fungsi matematika intinya. Sebagai jumlahan tak hingga dari suku-suku yang nilainya dihitung dari turunan fungsi tersebut.
Pada kelas kali ini, Dosen meminta Mahasiswa mengaproksimasikan nilai dari Sin(pi/7). Menggunakan rumus umum diatas. Pola didapat yaitu -x^2/2n(2n+1). Masukkan ke dalam Microsoft Excel. Simsalabim. Jawaban pun dapat dicari serinci mungkin. Kesimpulan blog saya kali ini. Hidup ini mudah. Sebetulnya. Hanya perlu perbanyak membaca. Jadi paham bagaimana cara menggunakannya. Ilmu dasar, terutama teknologi. Because, that's why it does exist. Makes everything easier.
Pertemuan 2, 10 September 2019
Jangan sia-siakan waktu satu detik pun. Tidak ada yang tahu kapan rejeki datang. Mungkin di detik tersebut. Seperti Pandji Pragiwaksono. Saat masih menjadi penyiar Hard Rock FM Bandung. Begitu tertanam pengalaman Pandji di hidup saya. Hari ini pun saya mendapat ilmu penting. Pseudocode.