Difference between revisions of "Daniswara Azka Surjaatmadja"
| Line 42: | Line 42: | ||
User Question : | User Question : | ||
| + | |||
Can you derive finite element equations from 1D PDE governing equations using weighted residual in a very simple way along with an example. | Can you derive finite element equations from 1D PDE governing equations using weighted residual in a very simple way along with an example. | ||
| + | |||
ChatGPT Answer : | ChatGPT Answer : | ||
| + | |||
| + | [[File:chatgpt_1.png]] [[File:chatgpt_2.png]] [[File:chatgpt_3.png]] | ||
| + | |||
| + | User Question : | ||
| + | |||
| + | Can you provide with algorithm, flow chart and python code. | ||
| + | |||
| + | ChatGPT Answer : | ||
| + | |||
| + | Algorithm | ||
| + | |||
| + | [[File:Algoritma_chatgpt.png]] | ||
| + | |||
| + | Flow Chart | ||
| + | |||
| + | [[File:flowchart_chatgpt.png]] | ||
| + | |||
| + | Python Code | ||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | # Problem parameters | ||
| + | L = 1.0 # Length of the domain | ||
| + | k = 1.0 # Thermal conductivity | ||
| + | u_0 = 0.0 # Boundary condition at x = 0 | ||
| + | u_L = 100.0 # Boundary condition at x = L | ||
| + | N = 4 # Number of elements | ||
| + | f = 10.0 # Constant heat source | ||
| + | |||
| + | # Derived parameters | ||
| + | num_nodes = N + 1 # Number of nodes | ||
| + | node_coords = np.linspace(0, L, num_nodes) # Node coordinates | ||
| + | |||
| + | # Initialize global stiffness matrix K and load vector F | ||
| + | K = np.zeros((num_nodes, num_nodes)) | ||
| + | F = np.zeros(num_nodes) | ||
| + | |||
| + | # Element length (assume uniform) | ||
| + | h = L / N | ||
| + | |||
| + | # Assemble the global stiffness matrix and load vector | ||
| + | for e in range(N): | ||
| + | # Local stiffness matrix for each element | ||
| + | K_elem = (k / h) * np.array([[1, -1], [-1, 1]]) | ||
| + | F_elem = (f * h / 2) * np.array([1, 1]) # Element load vector for constant f | ||
| + | |||
| + | # Assembly into global matrix and vector | ||
| + | K[e:e+2, e:e+2] += K_elem | ||
| + | F[e:e+2] += F_elem | ||
| + | |||
| + | # Apply Dirichlet boundary conditions | ||
| + | K[0, :] = 0; K[0, 0] = 1; F[0] = u_0 # u(0) = u_0 | ||
| + | K[-1, :] = 0; K[-1, -1] = 1; F[-1] = u_L # u(L) = u_L | ||
| + | |||
| + | # Solve the system of equations | ||
| + | u = np.linalg.solve(K, F) | ||
| + | |||
| + | # Display the solution | ||
| + | print("Nodal temperatures:", u) | ||
| + | print("Node positions:", node_coords) | ||
| + | |||
| + | # Optional: Plot the result | ||
| + | import matplotlib.pyplot as plt | ||
| + | plt.plot(node_coords, u, '-o', label='Temperature distribution') | ||
| + | plt.xlabel('Position along the rod') | ||
| + | plt.ylabel('Temperature') | ||
| + | plt.title('1D Heat Conduction using FEM') | ||
| + | plt.legend() | ||
| + | plt.show() | ||
Revision as of 16:56, 4 November 2024
BIODATA
Perkenalkan, nama saya Daniswara Azka Surjaatmadja, mahasiswa Magister Teknik Mesin di Universitas Indonesia dengan NPM 2406508353. Saat ini, saya fokus pada bidang fire protection system pada bangunan gedung. Melalui studi ini, saya berupaya mendalami aspek-aspek perlindungan kebakaran yang esensial untuk memastikan keamanan dan keandalan struktur bangunan. Saya berharap pengetahuan dan pengalaman ini dapat menjadi kontribusi signifikan dalam meningkatkan standar keselamatan bangunan di masa mendatang.
Pertemuan 1 - Komputasi Teknik (Selasa, 29 Oktober 2024)
Pembuatan akun air.eng.ui.ac.id untuk sebagai fasilitas kegiatan belajar untuk mata kuliah komputasi teknik. Semua catatan mengenai kegiatan kuliah dicatat pada wiki untuk memudahkan dalam mengarsip semua catatan yang berkaitan dengan perkuliahan komputasi teknik.
Perkenalan terhadap metode DAI5 yang dikembangkan oleh Pak DAI untuk menyelesaikan permasalahan yang mungkin dihadapi. Metode DAI5 merupakan pendekatan conscious thinking yang menggunakan kesadaran secara penuh tentang eksistensi adanya Tuhan, dengan diawali niat untuk mendekatkan diri dan mengingat kepada Tuhan dalam melakukan penyelesaian masalah. Tahapan DAI5 terdiri dari Intention, Initial Thinking, Idealization dan Instruction Set. DAI5 juga mengintegrasikan antara hardware, brainware, software (hasil pemikiran) dan heartware (kalbu).
Framework DAI5 adalah pendekatan penyelesaian masalah berbasis conscious thinking, yang berfokus pada kesadaran penuh dalam setiap tahap proses pemecahan masalah. Tujuan DAI5 adalah untuk menciptakan solusi yang komprehensif dan berdampak positif, baik secara teknis maupun sosial, dengan melibatkan aspek-aspek penting seperti niat (intention), pemahaman awal (initial thinking), idealisasi (idealization), dan langkah-langkah instruksi (instruction set).
Adapun komponen dari framework DAI5, antara lain :
1.Intention
Ini adalah tahap awal di mana ditentukan niat dan tujuan yang jelas. Fokusnya adalah pada sila pertama Pancasila, yaitu Ketuhanan Yang Maha Esa, sehingga tujuan utama adalah mencari keridhaan Tuhan dalam menyelesaikan masalah. Intention bersifat subjektif dan hanya diketahui oleh masing-masing individu, dipengaruhi oleh latar belakang dan pengalaman pribadi.
2.Initial Thinking
Tahap ini melibatkan pemahaman mendalam tentang masalah yang akan diselesaikan. Dimulai dengan identifikasi masalah, pengumpulan informasi awal yang relevan, dan perumusan masalah secara detail. Tujuannya adalah untuk memperoleh gambaran besar dan memahami prinsip dasar yang mendasarinya.
3.Idealization
Di sini, kompleksitas masalah disederhanakan dengan membuat asumsi yang dapat dipertanggungjawabkan. Langkah ini membantu mengurangi variabel yang dianggap kurang penting, sehingga solusi yang terarah dapat tercapai.
4.Instruction Set
Tahap terakhir adalah pembuatan serangkaian langkah-langkah terstruktur berdasarkan model yang telah disederhanakan. Langkah ini bertujuan untuk menerapkan solusi dengan efektif sesuai hasil idealization sebelumnya, memberikan panduan yang jelas dalam penyelesaian masalah.
Framework DAI5 membantu dalam memahami konteks masalah secara holistik dan memberikan pendekatan yang lebih sadar dan efektif dibandingkan metode penyelesaian masalah lainnya, dengan menekankan pada brainware (kapasitas berpikir) dan heartware (nilai spiritual).
DAI5 berbeda dari metode lain, seperti DMAIC, Global 8D, dan PDCA, karena menambahkan dimensi kesadaran dan nilai spiritual dalam tiap tahapannya. Berbeda dengan DMAIC yang berbasis data atau PDCA yang iteratif, DAI5 tidak hanya teknis tetapi juga subjektif, menggabungkan pemahaman masalah dengan nilai brainware dan heartware. Hal ini memungkinkan solusi yang lebih holistik, memadukan aspek teknis dan kesadaran untuk menciptakan dampak yang lebih luas secara sosial dan etis. DAI5 cocok untuk pemecahan masalah yang membutuhkan pendekatan komprehensif yang mempertimbangkan tidak hanya hasil akhir, tetapi juga nilai-nilai yang membangun proses tersebut.
Tugas 1 - Komputasi Teknik
Pada tugas 1 Komputasi Teknik kami diarahkan oleh Pak DAI untuk melakukan diskusi dengan menggunakan ChatGPT mengenai finite element equation dari 1D PDE yang diselaraskan dengan DAI5 Framework. Berikut merupakan hasil diskusi saya dengan ChatGPT.
User Question :
Can you derive finite element equations from 1D PDE governing equations using weighted residual in a very simple way along with an example.
ChatGPT Answer :
User Question :
Can you provide with algorithm, flow chart and python code.
ChatGPT Answer :
Algorithm
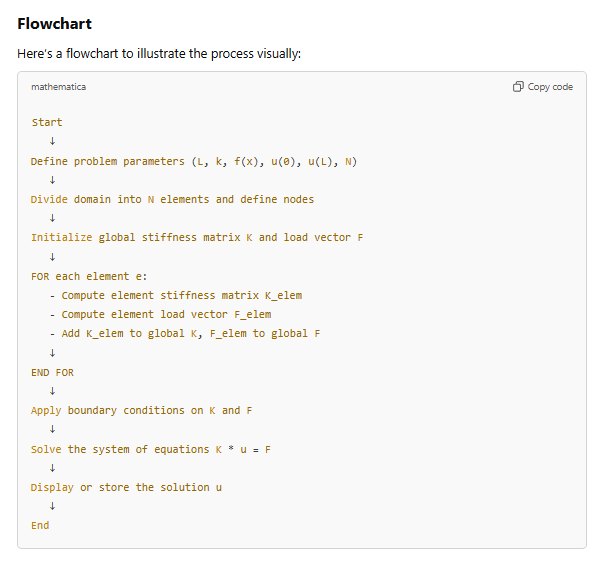
Flow Chart
Python Code
import numpy as np
- Problem parameters
L = 1.0 # Length of the domain k = 1.0 # Thermal conductivity u_0 = 0.0 # Boundary condition at x = 0 u_L = 100.0 # Boundary condition at x = L N = 4 # Number of elements f = 10.0 # Constant heat source
- Derived parameters
num_nodes = N + 1 # Number of nodes node_coords = np.linspace(0, L, num_nodes) # Node coordinates
- Initialize global stiffness matrix K and load vector F
K = np.zeros((num_nodes, num_nodes)) F = np.zeros(num_nodes)
- Element length (assume uniform)
h = L / N
- Assemble the global stiffness matrix and load vector
for e in range(N):
# Local stiffness matrix for each element K_elem = (k / h) * np.array([[1, -1], [-1, 1]]) F_elem = (f * h / 2) * np.array([1, 1]) # Element load vector for constant f
# Assembly into global matrix and vector K[e:e+2, e:e+2] += K_elem F[e:e+2] += F_elem
- Apply Dirichlet boundary conditions
K[0, :] = 0; K[0, 0] = 1; F[0] = u_0 # u(0) = u_0 K[-1, :] = 0; K[-1, -1] = 1; F[-1] = u_L # u(L) = u_L
- Solve the system of equations
u = np.linalg.solve(K, F)
- Display the solution
print("Nodal temperatures:", u) print("Node positions:", node_coords)
- Optional: Plot the result
import matplotlib.pyplot as plt plt.plot(node_coords, u, '-o', label='Temperature distribution') plt.xlabel('Position along the rod') plt.ylabel('Temperature') plt.title('1D Heat Conduction using FEM') plt.legend() plt.show()