Difference between revisions of "User:Umarfa"
m |
|||
| Line 1: | Line 1: | ||
| + | ==Tugas Komputasi Teknik Ke-1== | ||
'''DAI5''' | '''DAI5''' | ||
| Line 14: | Line 15: | ||
Kerangka kerja DAI5 dirancang untuk membuat topik yang kompleks menjadi lebih mudah dipahami, persuasif, dan dapat ditindaklanjuti, memandu pembaca dari data ke tindakan yang bermakna. | Kerangka kerja DAI5 dirancang untuk membuat topik yang kompleks menjadi lebih mudah dipahami, persuasif, dan dapat ditindaklanjuti, memandu pembaca dari data ke tindakan yang bermakna. | ||
| + | |||
| + | |||
| + | ---- | ||
| + | [[Question:]] ''To derive finite element equations from 1D partial differential equations (PDEs) using the weighted residual method, let's follow a straightforward example. We'll take a 1D Poisson equation as the governing equation and go through the process step by step.'' | ||
| + | |||
| + | [[Answer:]] | ||
| + | |||
| + | [[File:Gambar_Komputasi Teknik_Umar_1.png]] | ||
| + | [[File:Gambar_Komputasi Teknik_Umar_2.png]] | ||
| + | |||
| + | [[Question:]] ''Can you provide with algorithm, flow chart and python code'' | ||
| + | |||
| + | [[Answer:]] | ||
| + | |||
| + | [[File:Gambar_Komputasi Teknik_Umar_3.png]] | ||
| + | |||
| + | 2. Algorithm | ||
| + | |||
| + | [[File:Gambar_Komputasi Teknik_Umar_4.png]] | ||
| + | |||
| + | 3. Python Code | ||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | # Problem setup | ||
| + | L = 1.0 # Length of the domain | ||
| + | N = 10 # Number of elements | ||
| + | u0, uL = 0, 0 # Dirichlet boundary conditions at x=0 and x=L | ||
| + | f = lambda x: 1 # Source term f(x), assumed to be constant here | ||
| + | |||
| + | # Discretize the domain | ||
| + | nodes = np.linspace(0, L, N+1) # N+1 nodes | ||
| + | h = L / N # Element length | ||
| + | |||
| + | # Initialize global stiffness matrix K and load vector F | ||
| + | K = np.zeros((N+1, N+1)) | ||
| + | F = np.zeros(N+1) | ||
| + | |||
| + | # Element stiffness matrix and load vector (for linear elements) | ||
| + | Ke = (1/h) * np.array([[1, -1], [-1, 1]]) | ||
| + | Fe = lambda x1, x2: (h / 2) * np.array([f(x1), f(x2)]) | ||
| + | |||
| + | # Assemble the global matrix and vector | ||
| + | for i in range(N): | ||
| + | x1, x2 = nodes[i], nodes[i+1] # Nodes of the current element | ||
| + | F_e = Fe(x1, x2) # Element load vector | ||
| + | K[i:i+2, i:i+2] += Ke # Add element stiffness to global matrix | ||
| + | F[i:i+2] += F_e # Add element load to global vector | ||
| + | |||
| + | # Apply Dirichlet boundary conditions | ||
| + | K[0, :] = 0 | ||
| + | K[0, 0] = 1 | ||
| + | F[0] = u0 | ||
| + | |||
| + | K[N, :] = 0 | ||
| + | K[N, N] = 1 | ||
| + | F[N] = uL | ||
| + | |||
| + | # Solve the linear system | ||
| + | U = np.linalg.solve(K, F) | ||
| + | |||
| + | # Plot the solution | ||
| + | plt.plot(nodes, U, '-o', label="FEM Solution") | ||
| + | plt.xlabel("x") | ||
| + | plt.ylabel("u(x)") | ||
| + | plt.title("Solution to 1D Poisson Equation using FEM") | ||
| + | plt.legend() | ||
| + | plt.grid(True) | ||
| + | plt.show() | ||
| + | |||
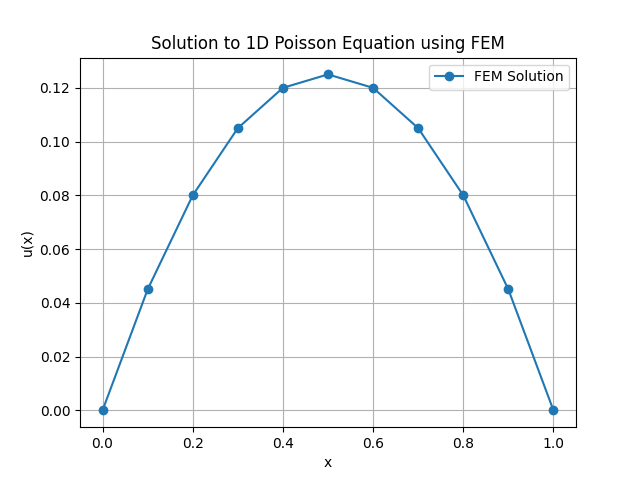
| + | Sehingga menghasilkan gradfik sebagai berikut: | ||
| + | |||
| + | [[File:Gambar_Komputasi Teknik_Umar_5.png]] | ||
| + | |||
| + | [[Question:]] | ||
| + | |||
| + | [[Answer:]] | ||
Revision as of 11:00, 4 November 2024
Tugas Komputasi Teknik Ke-1
DAI5
Kerangka kerja penulisan DAI5 adalah pendekatan terstruktur yang membantu penulis membuat tulisan yang jelas dan persuasif, terutama berguna untuk presentasi, proposal, dan argumen terstruktur lainnya. Kerangka kerja DAI5 terbagi menjadi lima komponen utama:
1. Data: Ini adalah fondasi faktual dari tulisan Anda. Data mencakup statistik, temuan penelitian, atau bukti apa pun yang mendukung pesan inti. Dengan mendasarkan tulisan Anda pada data yang kuat, Anda meningkatkan kredibilitas dan memberikan dasar konkret untuk argumen Anda.
2. Analisis: Di sini, Anda menafsirkan data yang disajikan. Analisis menjelaskan apa arti data tersebut, mengapa data tersebut penting, dan bagaimana data tersebut berhubungan dengan topik atau masalah Anda. Bagian ini membangun jembatan antara informasi mentah dan wawasan, membantu pembaca melihat relevansi data.
3. Wawasan (Insight): Wawasan adalah kesimpulan unik atau hasil dari analisis Anda. Wawasan menjawab pertanyaan “Lalu apa?”, menjelaskan implikasi dari data dan analisis. Wawasan harus jelas dan mudah diingat, memberikan alasan kepada pembaca untuk peduli dengan pesan tersebut.
4. Implikasi: Bagian ini mengkaji konsekuensi atau hasil potensial berdasarkan wawasan yang diberikan. Hal ini dapat mencakup dampak positif dan negatif, tren masa depan, atau tantangan yang diantisipasi. Implikasi membuat tulisan Anda berwawasan ke depan dan membantu pembaca mengantisipasi apa yang akan terjadi selanjutnya.
5. Implementasi: Pada langkah terakhir ini, Anda menyarankan langkah-langkah atau solusi yang dapat ditindaklanjuti. Implementasi memberikan pembaca jalan yang jelas ke depan, sehingga memudahkan mereka untuk menerapkan ide-ide atau mengambil tindakan berdasarkan wawasan Anda.
Kerangka kerja DAI5 dirancang untuk membuat topik yang kompleks menjadi lebih mudah dipahami, persuasif, dan dapat ditindaklanjuti, memandu pembaca dari data ke tindakan yang bermakna.
Question: To derive finite element equations from 1D partial differential equations (PDEs) using the weighted residual method, let's follow a straightforward example. We'll take a 1D Poisson equation as the governing equation and go through the process step by step.
Question: Can you provide with algorithm, flow chart and python code
2. Algorithm
3. Python Code
import numpy as np
import matplotlib.pyplot as plt
# Problem setup
L = 1.0 # Length of the domain
N = 10 # Number of elements
u0, uL = 0, 0 # Dirichlet boundary conditions at x=0 and x=L
f = lambda x: 1 # Source term f(x), assumed to be constant here
# Discretize the domain
nodes = np.linspace(0, L, N+1) # N+1 nodes
h = L / N # Element length
# Initialize global stiffness matrix K and load vector F
K = np.zeros((N+1, N+1))
F = np.zeros(N+1)
# Element stiffness matrix and load vector (for linear elements)
Ke = (1/h) * np.array([[1, -1], [-1, 1]])
Fe = lambda x1, x2: (h / 2) * np.array([f(x1), f(x2)])
# Assemble the global matrix and vector
for i in range(N):
x1, x2 = nodes[i], nodes[i+1] # Nodes of the current element
F_e = Fe(x1, x2) # Element load vector
K[i:i+2, i:i+2] += Ke # Add element stiffness to global matrix
F[i:i+2] += F_e # Add element load to global vector
# Apply Dirichlet boundary conditions
K[0, :] = 0
K[0, 0] = 1
F[0] = u0
K[N, :] = 0
K[N, N] = 1
F[N] = uL
# Solve the linear system
U = np.linalg.solve(K, F)
# Plot the solution
plt.plot(nodes, U, '-o', label="FEM Solution")
plt.xlabel("x")
plt.ylabel("u(x)")
plt.title("Solution to 1D Poisson Equation using FEM")
plt.legend()
plt.grid(True)
plt.show()
Sehingga menghasilkan gradfik sebagai berikut: